


| § О7. Дифференциальные уравнения с разрывной правой частью | 
|
— Г-голубчики, — сказал Федор Симеонович, разобравшись в почерках. — Это же п-проблема Бен Б-бецалеля. К-калиостро же доказал, что она н-не имеет решения.
— Мы сами знаем, что она не имеет решения, — сказал Хунта, немедленно ощетиниваясь. — Мы хотим знать, как ее решать.
— К-как-то ты странно рассуждаешь, К-кристо... К-как же искать решение, к-когда его нет? Б-бессмыслица какая-то ...
— Извини, Теодор, но это ты очень странно рассуждаешь. Бессмыслица — искать решение, если оно и так есть. Речь идет о том, как поступить с задачей, которая решения не имеет. Это глубоко принципиальный вопрос, который, как я вижу, тебе, прикладнику, к сожалению, не доступен.
А. и Б. Стругацкие.. Понедельник начинается в субботу
Как мы знаем, теорема Пеано гарантирует локальную разрешимость задачи Коши
| xў = f(t, x), x(t0) = x0 |
в случае непрерывной функции f. Если функция f непрерывной не является, то утверждение теоремы Пеано в общем случае не верно. Для иллюстрации рассмотрим два важных примера.
Первый пример представляет дифференциальные уравнения, у которых правая часть является "разрывной по t":
| xў = sign t. | (1) |
Поле направлений этого уравнения
изображено на
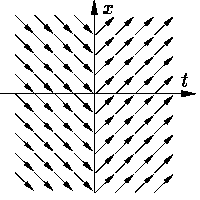
Другая ситуация имеет место для уравнения
| xў = sign x | (2) |
(здесь мы предполагаем, что sign 0 = 1). Его поле направлений см. на
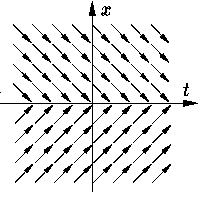
Принципиальное отличие этих двух примеров заключается том, что в первом случае поле направлений заставляет фазовую точку "прошивать" линию разрыва правой части и поэтому она находится на линии разрыва "нулевое время", тогда как во втором случае поле направлений устроено таким образом, что фазовой точке приходится пребывать на линии разрыва неопределенно долгое время.
Дифференциальные уравнения с разрывной правой частью помимо того, что они интересны сами
по себе, как математический объект, часто встречаются в механике, электротехнике, теории
оптимального управления и других областях науки. Источником дифференциальных уравнений с
разрывной правой частью в механике служат, например, механические системы с так называемым сухим
трением. Примером такой системы может служить тормозная колодка. Зависимость силы трения от
относительной скорости движения колодки качественно имеет вид, изображенный на
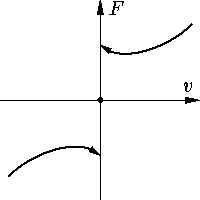 Рис. 3. |
 Рис. 4. |
Таким образом, классическое понятие решения
дифференциального уравнения (как функции, обращающей всюду на своей области определения
уравнение в тождество) нуждается в обобщении. Разумеется, основным требованием к такому обобщению
должно быть условие адекватности процессов, описываемых такими решениями, и соответствующих
физических (механических, биологических
Естественно также требовать, чтобы обобщенное решение в точках непрерывности правой части удовлетворяло уравнению в классическом смысле.
В этом очерке от читателя требуется знание основ теории функций действительного переменного, в частности, знакомство с понятиями меры Лебега, измеримой функции, интеграла Лебега.
Мы начнем с более простого случая, когда правая часть дифференциального уравнения
| xў = f(t, x) | (3) |
непрерывно зависит от x и может быть разрывной только по t. Тот факт, что в случае непрерывной функции f задача Коши для уравнения (3), порожденная начальным условием
| x(t0) = x0, | (4) |
эквивалентна интегральному уравнению
| (5) |
наводит на мысль назвать решением задачи
Один из наиболее известных и распространенных наборов условий на правую часть уравнения (3), при которых такой подход к расширению понятия решения оказывается содержательным в математическом плане и полезным и адекватным в приложениях выглядит следующим образом. Предполагается, что
1) функция x ® f(t, x) непрерывна почти при всех t;
2) функция t ® f(t, x) измерима при каждом x;
3) существует локально суммируемая функция
m:
Эти условия носят название условий
Каратеодори. Они, в частности, гарантируют, что если функция
Задача О7.1. Покажите, что функция
Решением Каратеодори
задачи
Задача О7.2. Покажите, что если f удовлетворяет
условиям Каратеодори, то функция x является
решением Каратеодори задачи
Задача О7.3. Покажите, что функция x(t) = x0 + |t| является решением Каратеодори уравнения (1).
Аналогом теоремы Пеано в данной ситуации является
Теорема Каратеодори.
Пусть функция f:
Доказывается эта теорема почти так же, как и
теорема Пеано.
Поясним, как ее можно доказать, используя, например,
приближения Тонелли.
Для произвольного натурального k определим на
| xk(t) = x0 при t О [t0 – T, t0] |
и рекуррентного (по i) соотношения
|
(6) |
(i = 1, ..., [T/k] + 1; здесь [a] — целая часть числа a). В силу условий Каратеодори, как отмечалось выше, подынтегральная функция в (6) измерима и суммируема, так что интеграл в правой части соотношения (6) имеет смысл. Далее, если положить
|
то, по-первых,
|
| Ј || x0 || + M(t0 + T) (t О [t0, t0 + T]) | (7) |
и, во-вторых,
|
| = |M(t) – M(t)| (t, t О [t0, t0 + T]). | (8) |
|
Условие (7) означает, что семейство функций {xk}
равномерно ограничено. А из оценки (8) вытекает,
поскольку функция M как интеграл от суммируемой функции непрерывна, и
следовательно, равномерно непрерывна, что семейство {xk}
равностепенно непрерывно. Поэтому по
|
Задача О7.4. Покажите, что условия Каратеодори обеспечивают возможность описанного предельного перехода.
На дифференциальные уравнения, удовлетворяющие условиям Каратеодори, переносится большинство утверждений качественной теории обыкновенных дифференциальных уравнений (см. задачи в конце очерка).
Перейдем теперь к уравнениям с "разрывной по x правой частью".
Задача О7.5. Покажите, что уравнение (2) не
имеет решения Каратеодори,
удовлетворяющего начальному условию
Основные идеи мы будем пояснять на простом классе
скалярных уравнений, а именно, будем предполагать, что
в уравнении (3) функция
f:
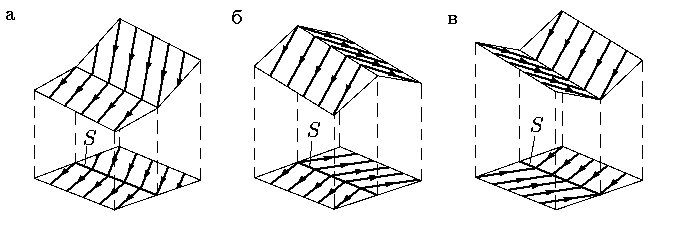
В случае а) интегральные кривые "прошивают"
кривую S за "нулевое время". Поэтому в этом случае
можно обойтись решениями
Каратеодори. Такое решение не будет дифференцируемым только в
изолированных точках, а именно, в момент, когда
В случае б), даже если поле направлений на S устроено таким образом, что фазовая точка может двигаться по кривой S, это движение не устойчиво в том смысле, что сколь угодно малые возмущения уводят точку из окрестности этой кривой.
Наконец, в случае, изображенном на
Большинство известных способов переопределения поля направлений на
кривой разрыва укладываются в следующую схему. Для каждой точки
| xў О F(t, x). | (9) |
Решением дифференциального включения
(9) на отрезке
Подчеркнем, что мы не требуем, чтобы решение было дифференцируемым в каждой точке своей области определения и чтобы оно в каждой точке удовлетворяло включению (9). Многочисленные примеры практики показывают плодотворность такого ослабления понятия решения.
Одна из возможных процедур построения многозначного
отображения f состоит в следующем. Для любых
|
Многозначное отображение F определим равенством
| F(t, x) = co F1(t, x); |
здесь co F1(t, x)
обозначает выпуклую замкнутую оболочку множества
Задача О7.6. Как выглядит отображение
F, если
Построенное нами многозначное отображение в большинстве
встречающихся на практике случаев обладает двумя важными
свойствами, гарантирующими разрешимость задачи Коши для дифференциального
включения (9) и, автоматически, разрешимость в описанном выше смысле
задачи Коши для дифференциального уравнения (3) с разрывной правой
частью. Это, во-первых, тот факт, что множество
Задача О7.7. Докажите, что (однозначное) отображение
j:
|
Задача О7.8. Докажите, что многозначное отображение
F: |
Задача О7.9. Пусть функция
f: R×R ® R
удовлетворяет описанным выше условиям,
Основу теории дифференциальных включений составляет следующая теорема о разрешимости задачи Коши:
Теорема Зарембы.
Пусть многозначное отображение F:
| x(t0) = x0, | (10) |
|
Эту теорему можно доказывать различными способами. Мы
покажем как ее можно доказать, используя аналог
ломаных Эйлера
Для любого натурального k положим
hk = |
| xўk(t)О F[tik,xk(tik)] при t О (tik, tki+1). | (11) |
Из ограниченности отображения F, очевидно, вытекает оценка
| |xўk(t)|Ј M при t О [t0, t0 + T]; |
в точках излома под xўk(t) понимается правая и левая производные. Из этой оценки и условия (10) следуют, как нетрудно видеть, неравенства
| |xk(t)| Ј |x0| + MT, |xk(t) – xk(t)| Ј M |t – t| (t, t О [t0, t0 + T]), |
означающие равномерную ограниченность и равностепенную непрерывность семейства функций
{xk}. Поэтому в силу теоремы
| jў(t) О F(t, j(t)) почти всюду на [t0, t0 + T]. | (12) |
План доказательства последнего утверждения приводится в следующих четырех задачах.
Задача О7.10. Покажите, что функция j удовлетворяет условию Липшица с константой M и, следовательно, почти всюду дифференцируема.
Задача О7.11. Докажите, что если y: [a, b] ® R — абсолютно непрерывная функция, то
|
где D — множество значений производных
функции y во всех точках отрезка
Задача О7.12. Докажите, что
|
при всех достаточно больших k.
Задача О7.13. Докажите соотношение (12).
В построенной на основе описанного приема теории дифференциальных уравнений с разрывной ("по x") правой частью имеют место аналоги многих утверждений стандартной теории обыкновенных дифференциальных уравнений (см. задачи в конце очерка).
Литературные указания. Теорию уравнений с "разрывной
по t правой частью" можно найти, напр. в
[Коддингтон — Левинсон,
Сансоне].
Современному состоянию теории уравнений с разрывной правой частью полностью посвящена книга
[Филиппов].
Основной поставщик задач в этой области — теория нелинейных колебаний
и теория автоматического регулирования (см.
[
Задачи.
О7.14. Докажите, что функция f(t, x) =
О7.15. Перенесите утверждения § 3.1 на линейные системы с локально суммируемыми коэффициентами.
О7.16. Пусть функция f удовлетворяет условиям
Каратеодори и обобщенному
условию Липшица с локально суммируемой функцией M.
Докажите, что задача
О7.17. Докажите, что в условиях задачи О7.16 корректно определен оператор сдвига по траекториям уравнения (3).
О7.18. Докажите, что в условиях теоремы Каратеодори множество
решений
задачи
О7.19. Докажите, что в условиях теоремы Каратеодори каждое
решение задачи
О7.20. Сформулируйте докажите теорему о нестрогих дифференциальных неравенствах с производными числами в случае, когда f удовлетворяет условиям Каратеодори.
О7.21. Сформулируйте и докажите какое-нибудь содержательное утверждение о непрерывной зависимости решений Каратеодори от параметра.
В следующих трех задачах предполагается, что
f: R ®
R — функция, имеющая в точке
| xў = f(x), x(t0) = x0 | (13) |
(в описанном в очерке смысле).
О7.22. Докажите, что решение задачи (13) единственно,
если
О7.23. Докажите, что если
fk: R ® R —
последовательность удовлетворяющих условию Липшица функций
таких, что при некотором M и всех
|
и
|
а jk: [t0, t0 + T] ® R — последовательность (классических) решений задачи Коши
| xў = fk(x), x(t0) = x0, |
то
|
(14) |
О7.24. Рассмотрим следующую задачу Коши для дифференциального уравнения с запаздывающим аргументом:
| (15) |
| (16) |
Ее решением будем называть абсолютно непрерывную функцию
jk:
О7.25. Докажите, что в условиях теоремы Зарембы каждое
решение задачи
О7.26. Пусть f: R ®2R — многозначная функция, определяемая равенством
|
Докажите, что множество равномерных пределов последовательностей решений задачи Коши
| xў О f(x), x(0) = 0 |
на отрезке [0, T] совпадает со множеством решений задачи Коши
| xў О F(x), x(0) = 0, |
где F(x) = co f(x).
|
О7.27. Докажите, что если g:
Rn ® R —
непрерывная положительная функция, а F: |
| xў О F(x) |
совпадает со множеством траекторий включения
| xў О g(x)F(x) |
и, наоборот. (Здесь под g(x)F(x)
понимается, как обычно, множество
|
О7.28. Пусть F: R×R
® 2R —
полунепрерывное сверху многозначное отображение
с выпуклыми замкнутыми образами. Каждой функции
|
О7.29. Покажите, что в условиях предыдущей задачи оператор
F полунепрерывен сверху, его образы выпуклы
и замкнуты и он вполне непрерывен
в следующем смысле: для любого ограниченного множества
File based on translation from
TEX by TTH,
version 2.32.
Created On 16 Jan 2000, 21:44.
Last modified 23 Apr 2002.