


| § О35. Дифференциальные уравнения с запаздывающим аргументом | 
|
Историк — человек,задающий вопросы о прошлом. Обычно думают, что он задает вопросы исключительно о прошлом, о прошлом, которое мертво и ушло и ни в каком смысле не присутствует в настоящем. Мне не понадобилось особенно углубляться в историческую мысль, чтобы понять ошибочность подобного мнения.
Р.Дж. Коллингвуд. Автобиография
Многочисленные процессы, основанные на передаче массы, энергии,
информации (например, наследственной)
Во многих случаях исключение запаздывания из рассмотрения, тем не
менее, позволяет адекватно описывать реальные процессы. Но иногда
неучитывание запаздывания приводит к абсурдным (или, по крайней
мере, не эквивалентным реальности) выводам. Рассмотрим в качестве
примера систему автоматического регулирования ("идеальный предсказатель"),
схема которого изображена на
| y(t) = v(t – 1). | (1) |
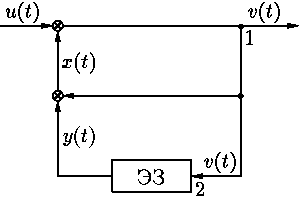
Работа этой системы описывается, очевидно, уравнениями
| v(t) = u(t) + x(t), | (2) |
| x(t) = v(t) + y(t). | (3) |
Подставляя (1) в (3), а
затем получившееся выражение для
| u(t) = –v(t – 1), | (4) |
или, заменяя t – 1 на t, а t на t + 1, уравнение
| u(t + 1) = –v(t). |
Таким образом, значение u(t + 1) входного сигнала в
"будущий" момент времени
Абсурдность полученного вывода обусловлена наличием неучтенного
реально существующего малого запаздывания при передаче сигналов по
линиям системы (например, от
| v(t) = u(t – e) + x(t – e), |
| x(t) = v(t – e) + y(t – e), |
а уравнение (4) — вид
| v(t) = u(t – e) + v(t – 2e) + v(t – 1 – 2e), |
уже не противоречащий принципу причинности.
Таким образом, некоторые процессы не могут быть адекватно описаны
обыкновенными дифференциальными уравнениями (
| xў(t) = f[t, x(t), x(t – h)], | (5) |
в котором x — неизвестная функция независимого аргумента t,
Простейшим примером процесса, описываемого дифференциальным уравнением с запаздывающим аргументом, может служить уравнение развития биологической популяции. Если считать, что скорость прироста популяции пропорциональна ее численности x(t) в настоящий момент, то мы получим известное уравнение Мальтуса или уравнение мальтузианского роста
| xў(t) = Cx(t). |
Если же исходить из (более реального) предположения о том, что скорость прироста пропорциональна численности лишь половозрелых особей (скажем, имеющих не меньший, чем h возраст), то мы придем к дифференциально-разностному уравнению
| xў(t) = Cx(t – h), |
поскольку величина x(t – h),
равная численности популяции в момент
Решением дифференциально-разностного
уравнения (5) на отрезке
| xў(t0) = f[t0, x(t0), x(t0 – h)]. |
В правую часть входит в этом случае неопределенная величина
При таком определении понятия решения наблюдается
аналогия с обыкновенными дифференциальными уравнениями; а именно,
решение уравнения (5) на отрезке
Начальной задачей (или
задачей Коши) для дифференциально-разностного
уравнения (5) называется задача о нахождении
решения x уравнения (5), совпадающего
на отрезке
| xў(t) = f[t, x(t), x(t – h)], t О [t0, t0 + T], | (6) |
| x(t) = j(t), t О [t0 – h, t0]. | (7) |
Оказывается, если функция f непрерывна и удовлетворяет по второму аргументу условию Липшица:
| |f(t, x1, y) – f(t, x2y)| Ј L|x1 – x2|, |
а функция j непрерывна на отрезке
Доказательство этой теоремы существования и единственности
основывается на так называемом методе шагов.
Суть его заключается в следующем. Будем сначала искать решение задачи
|
xў(t) = f[t,
x(t), j(t – h)]
| (8) |
Очевидно, функция f1(t, x) удовлетворяет
условиям теоремы
| x(t0) = j(t0). |
Тогда, как легко видеть, функция x1,
равная j на отрезке
| xў(t) = f[t, x(t), x(t – h)], t О [t0 + h, t0 + 2h], |
| x(t) = j1(t), t О [t0, t0 + h]. |
Таким способом решение задачи
Задача О35.1. Докажите единственность полученного решения.
Задача О35.2. Постройте решение задачи Коши
| xў(t) = x(t) + x(t – 1), t О [0, 3], |
| x(t) є 1, t О [–1, 0]. |
Одним из главных отличий дифференциальных уравнений с запаздывающим аргументом от обыкновенных дифференциальных уравнений является тот факт, что решения первых, вообще говоря, не допускают продолжения влево от начального отрезка, тогда как для вторых положительное и отрицательное направления времени полностью равноправны. Действительно, рассмотрим, например, уравнение
| xў(t) = x(t – 1) |
и попытаемся найти его решение на отрезке
| x(t) є 1. |
Заменив t – 1 на s
и считая, что s О
| x(s) = xў(s + 1) = (1)ў = 0, |
так как s + 1 О [–1,0] при
s О [–2, –1]. Таким образом,
"решение" терпит разрыв в точке
|
Тот факт, что решение уравнения (5) вправо
однозначно определяется его поведением на отрезке длины h
наводит на мысль, что фазовым пространством уравнения (5)
естественно считать не пространство R, а пространство
|
| [gt0t(j)](s)= y(t + s) (s О [–h, 0]), |
где y — решение уравнения (5), удовлетворяющее условию
| x(t) = j(t – t0) при t О [t0 – h, t0]. |
|
Подчеркнем, что в силу указанной выше невозможности в общем случае
продолжать решение уравнения (5) влево, оператор
gt0tпри
|
Задача О35.3. Докажите, что оператор сдвига по
траекториям уравнения (5) при
Все проведенные выше рассмотрения легко переносятся на случай систем дифференциальных уравнений с несколькими запаздываниями вида
| xў(t) = f[t, x(t), x(t – h1), ..., x(t – hk)], | (9) |
где f: R×Rn(k+1)
® Rn; h1, ...,
hk — положительные числа. Нужно только положить
Задача О35.4. Найдите решение задачи Коши
| xў(t) = tx(t) + x(t – 1) + x(t – Ц2), t О [0, 2], |
| x(t) = –t, tО [–Ц2, 0]. |
Задача О35.5. Сформулируйте и докажите теорему существования и единственности решения задачи Коши для уравнения (9).
Перейдем теперь к описанию линейных дифференциальных уравнений с запаздывающим аргументом. Начнем с автономных уравнений. Простейшим их представителем является уравнение
| xў(t) = ax(t) + bx(t – h), | (10) |
в котором h > 0, а a и b — произвольные
вещественные числа. Попытаемся строить
теорию линейных уравнений по аналогии с теорией
обыкновенных дифференциальных уравнений.
Напомним, что любое решение
линейного автономного обыкновенного дифференциального уравнения является
линейной комбинацией решений вида
| lelt = aelt + bel(t–h). |
Обозначив через q комплексную функцию комплексного аргумента, задаваемую формулой
| q(l) = l – a – be–lh, |
получим
| q(l)elt = 0. |
Очевидно теперь, что функция elt является решением уравнения (10) в том и только том случае, если l является нулем функции q. Функцию q называют характеристическим квазиполиномом или характеристической функцией уравнения (10), уравнение
| q(l) = 0 | (11) |
— характеристическим уравнением, а его решения — характеристическими значениями (или числами, или корнями) уравнения (10).
Если же подставить в уравнение (10) функцию
|
(здесь q(j) — j-ая производная функции q). Для выполнения последнего равенства, очевидно, необходимо и достаточно выполнения равенств
| q(l) = qў(l) = ... = q(l)(l) = 0. |
Таким образом, чтобы функция tlelt была решением уравнения (10) необходимо и достаточно, чтобы l было корнем характеристического уравнения не меньшей чем l кратности.
До настоящего момента аналогия с обыкновенными дифференциальными
уравнениями была полной. Однако, характеристическое уравнение
(11) имеет в общем случае бесконечное
множество корней (нетривиальное утверждение!) Поэтому множество
решений уравнения (10) (в отличие от множества
решений линейного обыкновенного дифференциального уравнения)
бесконечномерно,
Таким образом, любое решение уравнения (11),
вообще говоря, нельзя представить в виде линейной комбинации
конечного числа решений вида
Задача О35.6. Пусть q — характеристический квазиполином уравнения
| xў(t) = bx(t – 1). | (12) |
|
Докажите, что: а) если b № e,
то q не имеет кратных корней; |
Некоторые факты теории обыкновенных дифференциальных уравнений, конечно же, переносятся на линейные уравнения с запаздывающим аргументом почти без изменений. Например, легко доказывается, что общее решение линейного неоднородного уравнения
| xў(t) = a(t)x(t) + b(t)x(t – h) + f(t) |
является суммой частного его решения и общего решения соответствующего однородного уравнения (ср.). Но многие утверждения, верные для обыкновенных дифференциальных уравнений, для уравнений с запаздывающим аргументом просто не верны. Один пример такого утверждения мы уже привели выше (бесконечномерность множества решений). Еще один пример связан со следующим очевидным утверждением теории обыкновенных дифференциальных уравнений. Линейное автономное уравнение первого порядка
| xў = ax | (13) |
(a О R) не может иметь ненулевых периодических решений. Для уравнения с запаздыванием
| (14) |
это уже не так. Уравнение (14), очевидно, имеет
семейство 2p-периодических
решений вида
Подчеркнем, еще раз что дифференциальные уравнения с запаздывающим аргументом обыкновенными дифференциальными уравнениями не являются. По своим свойствам они ближе к дифференциальным уравнениям в частных производных.
Литературные указания. Литература по теории дифференциальных
уравнений с запаздыванием велика. Основные ссылки здесь таковы:
[Беллман — Кук,
Мышкис,
Норкин,
Пинни,
Задачи.
О35.7. Докажите, что если
| xў(t) = ax(t) + bxў(t – 1), t і 0, |
| x(t) = j(t), t О [–1, 0]. |
(j О C[–1, 0]) ограничено.
О35.8. Докажите, что любое решение
уравнения
О35.9. Приведите пример уравнения вида
О35.10. Для обыкновенного дифференциального уравнения
О35.11. Пусть j О C[–1, 0]. Единственно ли решение задачи Коши
| xў(t) = 2Ц|x(t – 1)|, t О [0, 2], |
| x(t) = j(t), t О [–1, 0]? |
При каких j решение задачи Коши
| xў(t) = 2Ц|x(t)| + 2Ц|x(t – 1)|, t О [0, 2], |
| x(t) = j(t), t О [–1, 0] |
неединственно?
О35.12. Пусть f: R3
® R непрерывна и удовлетворяет
условию Липшица по второму
аргументу,
| xў(t) = f(t, x(t), x[t – h(t)]), t і 0, |
| x(t) = j(t), t О [–h2, 0] |
однозначно разрешима.
О35.13. Пусть в условиях предыдущей задачи
О35.14. Рассмотрим задачу Коши
| xў(t) = f[t, x(t – h)], t О [0, T], | (15) |
| x(t) = j(t), t О [ – h2, 0] | (16) |
(f: R×R ®
R). Для любой x О C[0, T]
такой, что
|
Докажите, что, начиная с номера N =
[T/h] + 1 (здесь
О35.15. Докажите, что задача Коши
| xў(t) = x(t)x(t – 1), t і 0, |
| x(t) = j(t), t О [ – 1, 0] |
при любой j О
C[–1, 0] однозначно разрешима.
Найдите при всех
| xў(t) = x2(t) + x(t – h), t і 0, |
| x(t) = 1, t О [–h, 0]. |
|
О35.16. При каких a оператор
сдвига g20: |
| xў(t) = ax(t – 1) + 1 |
является сжимающим?
О35.17. Рассмотрим задачу Коши
| xў(t) = f(t, x(t), x[t + h(t)]), t О [0, T], | (17) |
| x(t) = j(t), t О [–h, 0] | (18) |
где f: R3 ®
R — непрерывная удовлетворяющая
условию Липшица
по второму и третьему аргументам функция, а
|
Для любой x О
Cj[0,T] определим
функцию
|
Докажите, что:
а) J: Cj[0, T]
® Cj[0,
T];
О35.18. Уравнением нейтрального типа называется уравнение вида
| xў(t) = f[t, x(t – h), xў(t – h)]. | (19) |
Задачей Коши на отрезке [0, T]
для этого уравнения называется задача о нахождении непрерывно
дифференцируемой на отрезке
| x(t) = j(t), t О [–h, 0] |
(j О C1[0, T]). Покажите, что для разрешимости этой задачи необходимо выполнение так называемого условия "склейки"
| jў(t) = f[t, j( – h), jў(–h)]. |
Докажите, что если f непрерывна и выполнено условие
склейки, то задача Коши для уравнения (19)
однозначно разрешима при любой j О
О35.19. Пусть j О C[–h, 0]. Докажите, что решение задачи Коши
| xў(t) = ax(t) + bx(t – h), t і 0, |
| x(t) = j(t), t О [–h, 0] |
О35.20. Выпишите характеристический квазиполином для уравнения
|
(ai, bi
О R, hi
і 0). Докажите, что найдется M
такое, что все его корни лежат в полуплоскости
О35.21. Докажите, что если {li} — произвольная последовательность различных характеристических корней уравнения
| xў(t) = ax(t) + bx(t – h), |
то Re li
О35.22. Пусть y — решение задачи Коши
| xў(t) = ax(t) + bx(t – h) + f(t), t і 0, |
| x(t) = j(t), t О [–h, 0] |
(j О C[–h,
0]). Докажите существование таких M и a,
что при всех
|
File based on translation from
TEX by TTH,
version 2.32.
Created 26 Mar 2000, 15:58.
Last modified 4 May 2002.