§ 2.2. Сведения из алгебры и анализа

В этом параграфе собраны необходимые определения и факты, которые изучались или будут изучаться в курсах алгебры и математического анализа.

2.2.1. Линейные пространства. В курсе дифференциальных уравнений мы будем иметь дело со следующими линейными пространствами.

1) Rⁿ — координатное n-мерное пространство с полем скаляров R.

2) Cⁿ — комплексное координатное n-мерное пространство над полем C комплексных чисел.

Мы будем также иногда применять обозначения

K = (R или C), Kn = (Rn или Cn).

3) C = C(J, Kⁿ) — пространство непрерывных функций x: J ® Kⁿ, J М R — промежуток.

4)C^m = C^m(J, Kⁿ) — пространство m раз непрерывно дифференцируемых функций из C.

2.2.2. Скалярное произведение. В Kⁿ определено скалярное произведение

(x, y) = N е i = 1 xiyi,

которое в вещественном случае выражается формулой

(x, y) = N е i = 1 xiyi,

Оно порождает евклидову норму (длину) вектора

||x||2 =   __ Цx2 =   ____ Ц(x, x)

которая обладает следующими свойствами:

(а) ||x||₂ і 0, ||x||₂ = 0 Ы x = 0,

(б) ||ax||₂ = |a|·||x||₂,

(в) ||x+y||₂ Ј ||x||₂ + ||y||₂.

2.2.3. Другие нормы в Kⁿ. В Kⁿ можно рассматривать и другие нормы, например,

||x||1 = N е i = 1 |xi|,

||x||Ґ = max i = 1, 2, ..., n |xi|

(и бесконечно много других).

Для произвольной нормы (по определению, функции, удовлетворяющей условиям (а) – (в)) в Kⁿ мы будем употреблять обозначение ||x||. В конечномерном пространстве любые две нормы || · ||ў и || · ||ўў эквивалентны (пишут || · ||ў  ~  || · ||ўў), т. е. для них существуют положительные константы m и M такие, что

m||x||ў Ј ||x||ўў Ј M||x||ў

для любого x.

Сходимость последовательности по норме эквивалентна в Kⁿ сходимости покоординатной:

(||xn – x|| ® 0 при n ® Ґ) Ы"(i) [xin ® xi при n ® Ґ].

2.2.4. Нормы в C и C^m. Если J = [a, b], то в C и C^m можно ввести нормы с помощью формул

||x|| = sup t О [a, b] ||x(t)||,

||x||m = ||x|| + ||xў|| + ... + ||x(m)||.

В бесконечномерных пространствах, каковыми являются C и C^m, существуют неэквивалентные нормы. Например, следующая норма в C не эквивалентна || · || (докажите):

||x||L1 = т b a ||x(t)|| dt.

Сходимость в норме || · || эквивалентна равномерной сходимости, а в норме || · ||_m — равномерной сходимости функций и их производных до порядка m включительно.

Напомним определение равномерной сходимости функций x_k: J ® Kⁿ к функции x: J ® Kⁿ (J М R):

xk(t) сходится равномерно на J к x(t) при k ® Ґ

по определению означает, что

"(e > 0)$(N О N)"(k і N)"(t О J)[||xk(t) – x(t)|| < e]

и обозначается

xk(t) Ю x(t) при k ® Ґ (t О J).

От определения точечной сходимости, т. е. сходимости при каждом фиксированном t О J оно отличается положением квантора общности по t:

xk(t) точечно сходится на J к x(t) при k ® Ґ

по определению означает, что

"(t О J)"(e > 0)$(N О N)"(k і N)[||xk(t) – x(t)|| < e]

и обозначается

xk(t) ® x(t) при k ® Ґ (t О J).

На рис. 1 приведены примеры неравномерно точечно (слева) и равномерно (справа) сходящихся к нулевой функции на J = [0, 1] последовательностей.

Рис. 1.

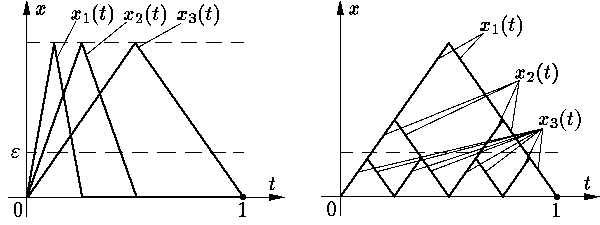
Предел равномерно сходящейся последовательности непрерывных функций есть непрерывная функция; при точечной сходимости непрерывность может не сохраняться (см. рис. 2).

Рис. 2.

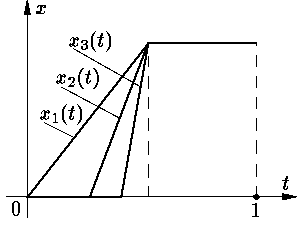
Пространство C полно: если последовательность x_k О C фундаментальна, т. е. ||x_k – x_p|| Ю 0 при k, p ® 0, то существует функция x О C, к которой она равномерно сходится: ||x_k – x|| Ю 0 при k ® Ґ.

Справедлива следующая теорема Вейерштрасса о дифференцировании: если x_k О C¹ (k = 1, 2, ...), x_k(t) ® x(t) при k ® Ґ и xў_k(t) Ю y(t) при k ® Ґ, то x О C¹ и xў(t) = y(t).

2.2.5. Линейные операторы и их нормы. Линейный оператор A — это отображение линейного пространства E₁ в линейное пространство E₂, удовлетворяющее условию: A(ax + by) = aAx + bAy.

Если пространства E₁ и E₂ нормированы, т. е. снабжены нормами || · ||₁ и || · ||₂, то можно определить норму оператора A условиями:

а) "(x О E₁) [||Ax||₂ Ј ||A||·||x||₁],

б) "(e > 0) $(x О E₁) [||Ax||₂ > (||A|| - e)||x||₁].

Для линейного оператора, действующего в бесконечномерных пространствах, может не существовать конечной нормы — такие операторы называются неограниченными, в отличие от ограниченных. Ограниченность линейного оператора эквивалентна его непрерывности в любой точке x₀, т. е. тому, что из ||x_k – x₀||₁ ® 0 при k ® Ґ следует ||Ax_k – Ax₀||₂ ® 0 при k ® Ґ. Любой линейный оператор, действующий в конечномерных пространствах, ограничен.

Норма линейных ограниченных операторов является нормой в пространстве таких операторов, т. е. удовлетворяет условиям (а) – (в) п. 2.2.2.

Линейный оператор, действующий из конечномерного пространства в конечномерное с заданными базисами, известным образом представляется в виде матрицы. Пространство прямоугольных матриц фиксированных размеров конечномерно и, следовательно, в нем любые две нормы эквивалентны. В частности,

||A|| ~   е i, j |aij| ~ max i, j |aij| ~ max i   е j |aij| ~ max j   е i |aij|,

где a_ij — элементы матричного представления оператора A.

2.2.6. Дифференцируемость и условие Липшица. Отображение f: D(f) М E₁ ® E₂ линейного нормированного пространства E₁ в линейное нормированное пространство E₂ называется дифференцируемым в точке x₀ О D(f), если существует такой линейный ограниченный оператор f ў(x₀): E₁ ® E₂, что

f(x) – f(x0) = f ў(x0)(x – x0) + w(x0, x) (x О D (f)),

где w(x₀, x)/||x – x₀||₁ ® 0 при ||x – x₀||₁ ® 0.

Теорема о среднем утверждает, что если отображение f дифференцируемо на D(f) и отрезок [x₀, x₁] = {(1 – t)x₀ + tx₁: t О [0, 1]} лежит в D(f), то

||f(x1) – f(x0)||2 Ј sup xО[x0, x1] ||f ў(x)||·||x1 – x0||1.

В частности, если область D(f) выпукла и производная ограничена:

||f ў(x)|| Ј L (x О D(f)),

то f удовлетворяет в D(f) условию Липшица с константой L:

||f(x1) – f(x0)||2 Ј L||x1 – x0|| (x1, x0 О D(f)).

Если f действует из D(f) М Rⁿ в R^k и дифференцируем, то координатные функции f_i(x) (i = 1, ..., k) также дифференцируемы и матричное представление A = f ў(x) в естественных базисах имеет вид:

aij = ¶fi(x) ¶xj  (i = 1, ..., k; j = 1, ..., n).

Это означает, в частности, что если все частные производные ¶f_i(x)/¶x_j ограничены в выпуклой области D(f) некоторой константой L₁, то f удовлетворяет в D(f) условию Липшица с какой-то константой L. Условию Липшица могут удовлетворять и недифференцируемые функции — см. пример в следующем пункте.

Общее соотношение между дифференцируемостью, условием Липшица и непрерывностью следующее (область выпуклая): существование и ограниченность производной влечет условие Липшица, которое, в свою очередь, влечет равномерную непрерывность.

Если выражение f(t, x) непрерывно по t при любом фиксированном значении x и удовлетворяет условию Липшица по x с константой, не зависящей от t, то оно непрерывно по совокупности переменных:

||f(tn, xn) – f(t0, x0)|| Ј ||f(tn, xn) – f(tn, x0)|| + ||f(tn, x0) – f(t0, x0)|| Ј

Ј L||xn – x0|| + ||f(tn, x0) – f(t0, x0)|| ® 0 при n ® Ґ.

2.2.7. Геометрический смысл условия Липшица. Для функции f: J М R ® R условие Липшица — это ограниченность по модулю угловых коэффициентов всех хорд графика функции f: условие

(|f(x) – f(y)| Ј L|x – y|)Щ(x № y)

очевидно эквивалентно условию

к к к f(x) – f(y) x – y к к к Ј L.

Выражение в левой части неравенства — это угловой коэффициент хорды (см. рис. 3a).

Рис. 3.

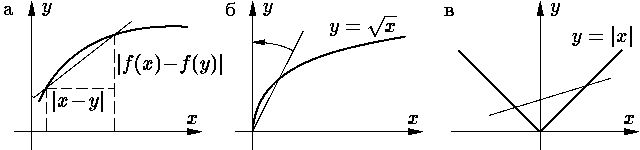
Например, функция y = Цx на отрезке [0, 1] не удовлетворяет условию Липшица, т. к. вблизи точки x = 0 хорды графика становятся сколь угодно близкими к вертикали (рис. 3б).

Функция y = |x| (не всюду дифференцируемая) удовлетворяет условию Липшица с константой L = 1, т. к. угловой коэффициент хорд графика, очевидно, по модулю не больше единицы (рис. 3в).

2.2.8. Контрольные вопросы

2.2.8.1. Найдите константы m и M, связывающие нормы || · ||₂, || · ||₁, || · ||_Ґ в Kⁿ.

2.2.8.2. Если функция f: Rⁿ ® Rⁿ удовлетворяет условию Липшица относительно какой-либо нормы в Rⁿ, то она удовлетворяет условию Липшица относительно любой нормы в Rⁿ?

2.2.8.3. Какие из перечисленных ниже функций f: R ® R и g:R² ® R² удовлетворяют условию Липшица:

f(x) = sin x; f(x) = e – x; f(x) = x2; f(x) = e-|x|x2; g(x) = (x1sin x2, 0); g(x) = x|x|sin x g(x) = (   ______ Цx12+ x22 ,   _______ Ц|x12– x22| ); g(x) = (e–|x1|x22, e–|x2|x12)?

File based on translation from T_EX by T_TH, version 2.32.
Created 3 Jan 2002, 21:55.
Last modified 11 Apr 2002.