


| § 2.1. Постановка задачи | 
|
В о п р о с: Началась ли наша работа? А если началась, то в чем она состоит?
О т в е т: Работа наша сейчас начнется, а состоит она в регистрации мира...
Даниил Хармс. Сабля
В настоящем параграфе мы дадим общее определение задачи Коши и обсудим постановку вопросов существования и единственности.
2.1.1. Постановка задачи Коши. Общий вид ОДУ без выделения вектора произвольных постоянных C таков (см. п. 1.1.2):
| F(t, J(m)x) = 0. | (1) |
Если (1) можно разрешить относительно старших
производных,
| x(m) = f(t, J(m–1)x), | (2) |
то путем увеличения числа неизвестных скалярных функций (см.
| xў = f(t, x). | (НС) |
Поэтому в дальнейшем основным объектом изучения будет именно нормальная система (НС).
Задача Коши, или начальная задача для уравнения (2) — это система, состоящая из (2) и начального условия
| J(m–1)x(t0) = y0 О R|m|, |
где t0 О R — начальный момент, y0 — начальное значение. Для (НС) начальное условие записывается в виде
| x(t0) = x0 О Rn. | (НУ) |
Геометрический смысл задачи Коши
(НС), (НУ)
заключается в том, чтобы во множестве всех интегральных кривых
системы (НС) найти ту, которая проходит через точку
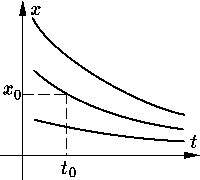
П р и м е р. Решение задачи Коши для линейного неоднородного уравнения
|
дается формулой
|
где
|
(см.
2.1.2. Постановка задач о существовании и единственности. В этой главе нас будут интересовать следующие вопросы, относящиеся к задаче Коши.
1) Вопрос о локальной разрешимости: имеет ли задача (НС), (НУ) решение на каком-либо промежутке J?
2) Вопрос о глобальной разрешимости: имеется ли у этой задачи решение, определенное на наперед заданном промежутке J?
3) Вопрос о единственности: можно ли утверждать, что любые два решения задачи (НС), (НУ) совпадают на общей части их области определения?
В § 2.3 мы докажем теорему Коши — Пикара, которая утверждает, что при выполнении определенных условий все эти вопросы имеют утвердительные ответы, однако сначала рассмотрим три примера, в которых дело обстоит иначе.
2.1.3. Пример отсутствия локальной разрешимости. Задача
| (3) |
| x(0) = 0 | (5) |
не имеет решения ни на каком промежутке J.
Д о к а з а т е л ь с т в о. Предположим противное: пусть
x =
Причиной выявленной "неприятности" является разрывность правой части уравнения (3) в точке x = 0.
2.1.4. Пример отсутствия глобальной разрешимости. Уравнение
| xў = x2 + 1 | (5) |
легко решается:
|
| arctg x = t + C, |
| (6) |
Подчеркнем, что (5) Ы (6).
Это означает, в частности, что вопрос о разрешимости
задачи (5), (4), скажем, на промежутке
Этот эффект связан с тем, что правая часть x2 + 1
уравнения (5) при
2.1.5. Пример отсутствия единственности.
Таким примером может служит, в частности, уравнение (15) из
| xў = 2Цx, |
правая часть которого определена при x і 0. У задачи Коши, соответствующей начальному условию (4), помимо нулевого имеется бесконечно много решений
|
Причина неединственности — в том, что правая часть этого уравнения в точке x = 0 имеет бесконечную производную по x.
2.1.6. Контрольные вопросы
2.1.6.1. Может ли решение j:
2.1.6.2. Будем говорить, что уравнение (НС) обладает
свойством единственности решения вправо
(соответственно, влево),
если задача Коши (НС), (НУ) при любых
2.1.6.3. Если уравнение (НС) обладает свойствами единственности решения вправо и влево, то любые два решения задачи Коши (НС), (НУ) совпадают на общей области определения?
File based on translation from
TEX by TTH,
version 2.32.
Created 3 Jan 2002, 15:18.
Last modified 8 Apr 2002.