


| § О11. Динамические системы | 
|
... представляется еще более истинным, что в природе все происходит по извечным законам математики — незыблемым и независимым...
Вольтер. Метафизический трактат
Простейшие свойства автономных (или, как их часто
называют, динамических) систем дифференциальных уравнений были
нами установлены в
| xў = f(x), | (1) |
отличающих такие системы от неавтономных.
|
Предполагается, что Rn ®
Rn и удовлетворяет условию
Липшица; поэтому решение задачи Коши
для уравнения (1) с любыми начальными данными определено на всей оси и
единственно. Через gts мы будем как всегда обозначать
оператор сдвига по траекториям
уравнения (1), а через |
| gt = gst+s |
при всех s О R. В терминах решений уравнения (1) этот факт эквивалентен тому, что сдвиг вдоль оси t любого решения уравнения (1) является его решением.
Напомним, что интегральной кривой уравнения (1)
мы называем график Gj
любого решения j в расширенном фазовом
пространстве
| Gj = {(t, x) О R×Rn: t О D(j), x = j(t)}, |
| Tj = {x О Rn: x = j(t), t О D(j)}, |
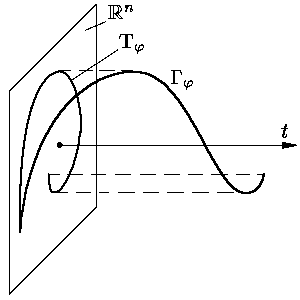
Задача О11.1. Докажите,что если две траектории отвечают непродолжимым решениям уравнения (1) и имеют общую точку, то они совпадают.
В дальнейшем мы под траекториями будем понимать только траектории отвечающие максимальным (непродолжимым) решениям системы (1).
Траекторию, соответствующую стационарному (
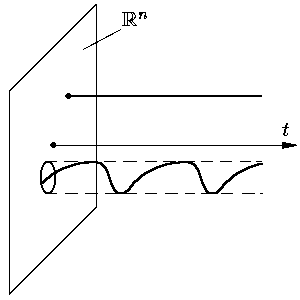
Имеет место следующая
Теорема о типах траекторий автономных систем. Каждая траектория системы (1) является либо стационарной точкой, либо циклом без самопересечений, либо траекторией без самопересечений.
Д о к а з а т е л ь с т в о. Пусть Tj —
отвечающая максимальному решению j
траектория системы (1). Если Tj
имеет самопересечение,
| j(t) = gtt[j(t)]= gqt+q-t[j(t)] = gqt+q-t[j(q)] = j[t + (q - t)] |
при всех t О R. Далее в доказательстве нам потребуются следующие утверждения.
Задача О11.2. Пусть j — непрерывная функция на R. Тогда множество всех ее периодов: а) образует аддитивную группу, б) является замкнутым.
Обозначим через T точную нижнюю грань множества положительных периодов
решения j. Альтернатива такова: либо
Задача О11.3. Приведите пример неавтономной системы, имеющей непериодическое решение, траектория которого имеет самопересечения, и пример автономной системы (правая часть которой по необходимости не удовлетворяет условию Липшица), имеющей периодическое решение минимального положительного периода T, порождающее цикл с самопересечением.
Задача О11.4. Докажите, что в одномерном случае траекториями автономной системы могут быть только множества вида: точка, открытый промежуток, открытый луч, вся прямая.
Теперь мы переходим к исследованию поведения решений при
Задача О11.5. Покажите,что
|
где черта означает замыкание множества в Rn.
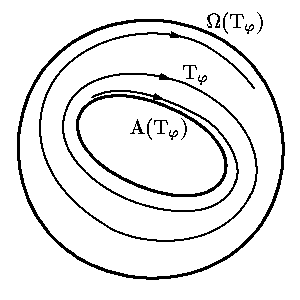
Структуру w-предельных множеств частично выясняет следующая
Теорема о структуре w-предельных
множеств. Для любого решения j
системы (1) множество
Д о к а з а т е л ь с т в о. Замкнутость
W(Tj)
очевидна в силу задачи О11.5.
Непустота вытекает из относительной
компактности ограниченных подмножеств конечномерного пространства, а компактность
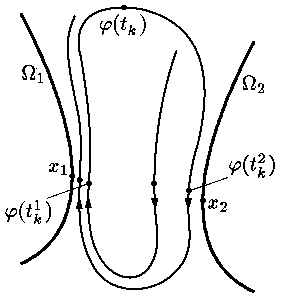
Для доказательства связности
W(Tj)
предположим противное. Тогда, по определению,
| r = inf{||x – y||: x О W1, y О W2} |
|
в силу замкнутости и ограниченности W1
и W2 положительно. Пусть
|
| j(tk1)® x1 О W1 и j(tk2)® x2 О W2 при k ® Ґ. |
Не теряя общности, можно считать, что при всех
| tk1< tk2< t1k+1 |
и
| inf{||j(t1k)– x ||: x О W1} < r/2, inf{||j(t2k)– x ||: x О W2} < r/2. |
|
В силу непрерывности j и замкнутости и ограниченности
W1 и W2 найдутся такие
|
|
(2) |
|
(см. |
Аналогичная теорема имеет место и для a-предельных множеств.
Множество M Н Rn
называется положительно (соответственно,
отрицательно) инвариантным множеством
уравнения (1)
(и порожденного им потока gt),
если
Задача О11.6. Докажите, что объединение любого семейства траекторий является инвариантным множеством. Наоборот, любое инвариантное множество есть объединение некоторого семейства траекторий.
Теорема об инвариантности предельных множеств. w- и a-предельные множества любой траектории инвариантны.
Д о к а з а т е л ь с т в о. Пусть
|
что и требовалось доказать.
Таким образом, предельные множества любой траектории состоят из траекторий системы (1).
Продолжая изучение поведения решений при
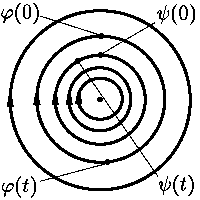
С асимптотической
устойчивостью дело обстоит еще хуже, а именно, всякое периодическое нестационарное
решение j
автономной системы
никогда(!) не бывает асимптотически устойчивым. В самом деле, начальные данные решений
В то же время, представляется физически естественным считать колебания математического маятника вблизи нижнего состояния равновесия устойчивыми: малые возмущения начальных данных приводят к малым изменениям амплитуды, фазы и частоты колебаний. В этом направлении мы и модифицируем понятия устойчивости и асимптотической устойчивости.
|
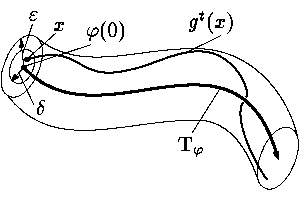
Полутраекторией
Tj+,
порожденной решением j,
будем называть часть траектории Tj,
отвечающую положительным значениям t. Решение j
системы (1) и соответствующую ему траекторию
Tj называют орбитально устойчивыми,
если для каждого |
| inf{||gt(x) – y ||: y О T+j}Ј e | (3) |
|
при всех t і 0. Соотношение (3)
означает, что при малых возмущениях начальных данных траектория решения остается в
e-окрестности полутраектории
Tj+
(см. |
|
Орбитально устойчивое решение j и
соответствующая траектория Tj
называются орбитально асимптотически
устойчивыми, если найдется такое |
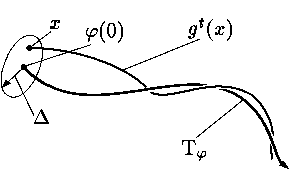
Предельным циклом называют цикл
Tj, для которого либо
|
Задача О11.7. Является ли цикл {(x1, x2) О R2: x21+ x22= 1} системы |
| xў1= – x2 + x1(1 – x21 – x22), |
| xў2= x1 + x2(1 – x21 – x22) |
предельным? Орбитально асимптотически устойчивым?
|
При исследовании устойчивости предельных циклов весьма полезным оказывается рассмотрение
так называемой функции последования. Строится она
следующим образом. Пусть |
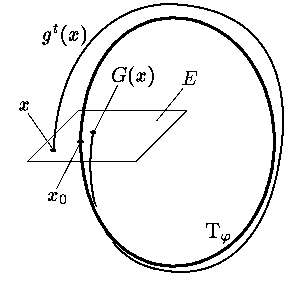
Задача О11.8. Докажите, что G(0) = 0 (здесь 0 — нуль пространства E). Пользуясь теоремой о непрерывной зависимости решений от начальных данных и теоремой о неявной функции, докажите, что в достаточно малой окрестности U нуля в E отображение G определено и непрерывно.
Роль, которую играет функция последования при исследовании орбитальной устойчивости, выясняется в следующем утверждении, доказательство которого мы оставляем читателю в качестве упражнения.
Теорема об орбитальной асимптотической устойчивости.
| || Gk(x)|| Ј q||x||. | (4) |
Тогда цикл Tj орбитально асимптотически устойчив.
Один достаточный признак асимптотической
орбитальной устойчивости предельного цикла дает формулируемая ниже
теорема
Пусть f непрерывно дифференцируема и пусть
| xў = A(t)x, | (5) |
где A(t) = df/dx|x=j(t).
Очевидно матрица A является T-периодической и поэтому, в частности,
система (5) является правильной по
Ляпунову. К сожалению, в случае нестационарного решения j
условия теоремы Ляпунова об устойчивости по
первому приближению никогда не бывают выполненными. Действительно,
как показывает дифференцирование тождества
Тем не менее, удается указать условия, при которых решение j будет орбитально асимптотически устойчивым. Точнее, имеет место
Теорема Андронова — Витта. Пусть нулевой
характеристический показатель
линеаризованной системы (5) однократен, а остальные характеристические
показатели этой системы отрицательны. Тогда решение j
орбитально асимптотически устойчиво. Более того, для любого
решения y, начинающегося достаточно близко к траектории
Tj, найдется число t
(называемое асимптотической фазой решения
y) такое, что
Доказательство этой теоремы мы опускаем. По поводу проверки условия отрицательности характеристических показателей сошлемся на задачу О21.14, в которой описывается спектр характеристических показателей линейной системы с периодическими коэффициентами в терминах ее оператора сдвига за период.
Наконец, заметим, что наличие асимптотической фазы
означает, что при
Литературные указания. Термин "динамическая система", в некотором смысле, является
синонимом термина "дифференциальное уравнение". Поэтому список литературы к
данному очерку весьма обширен. Мы перечислим здесь лишь классические учебники
[Арнольд,
Бибиков,
Задачи.
О11.9. Приведите примеры динамических систем
и их траекторий Tj
таких, что
О11.10. Приведите пример динамической системы в
R3 и ее траектории
Tj такой, что
О11.11. Докажите, что если j ограничено вправо, то
| inf{||j(t) – x||: x О W(T)} ® 0 при t ® Ґ. | (6) |
Приведите пример автономной системы и ее траектории Tj, для которой (6) не выполнено.
О11.12. Докажите, что замыкание и внутренность инвариантного множества являются инвариантными множествами.
О11.13. Докажите, что решение j системы
(1) периодично в том и только том случае, если
О11.14. Замкнутое непустое инвариантное множество системы (1) называется минимальным, если оно не имеет собственных инвариантных подмножеств системы (1). Приведите пример автономной системы и ее траектории, w-предельное множество которой не минимально. Докажите, что любой цикл является минимальным инвариантным множеством.
О11.15. Пусть
Tj — траектория системы (1).
Докажите, что если
О11.16. Докажите, что множество M Н Rn является инвариантным в том и только том случае, если вместе с каждой своей точкой оно содержит замыкание траектории, проходящей через эту точку.
О11.17. Докажите, что если
w-предельное
множество
| О11.18. Пусть
|
|
|
О11.19. Приведите пример траектории
Tj автономной системы, для которой:
|
Теорема Брауэра гласит: любое непрерывное отображение шара конечномерного пространства в себя имеет неподвижную точку.
О11.20. С помощью теоремы Брауэра докажите, что если система (1) имеет инвариантное множество гомеоморфное шару, то она имеет стационарную точку.
File based on translation from
TEX by TTH,
version 2.32.
Created 19 Jan 2000, 18:34.
Last modified 25 Apr 2002.