


| § О2. Дифференциальные и интегральные неравенства | 
|
Чем скорее проедешь, тем скорее приедешь.
Козьма Прутков. Мысли и афоризмы
С одним примером интегрального неравенства мы уже сталкивались — это
неравенство
| yў(t) Ј f[t, y(t)], y(t0) Ј x0 |
через решения задачи Коши
| xў = f(t, x), | (1) |
| x(t0) = x0. | (2) |
Дифференциальные и интегральные неравенства широко используются для получения различных оценок. Важные приложения нам встретятся в очерках О3 и О4.
Сначала мы покажем какого типа бывают утверждения о дифференциальных (и интегральных) неравенствах в скалярном случае, а затем уже поясним как они могут быть перенесены на случай систем дифференциальных (и интегральных) неравенств.
Итак, пусть f: R×R ® R — непрерывная функция.
Теорема о строгих дифференциальных неравенствах.
Пусть непрерывно дифференцируемая на отрезке
| yў(t) < f[t, y(t)], t О[t0, t0 + T], | (3) |
| y(t0) Ј x0, | (2) |
а x — определенное на [t0,
t0 + T] решение задачи
| y(t) < x(t). |
Для д о к а з а т е л ь с т в а, предположив противное, положим
| t = sup{s О (t0, t0 + T]: y(x) < x(x) при всех x О (t0, s)} |
(см.
|
Но тогда
|
|
Противоречие.
Задача О2.1. Восстановите детали доказательства. В частности, почему: (а) t > t0? (б) y(T) < x(T)?
Подчеркнем, что в некоторые моменты времени функция y может иметь бóльшую производную, чем функция x.
Задача О2.2. Приведите пример.
Если в (3) заменить строгое неравенство на нестрогое, то в случае
единственности решения задачи
Задача О2.3. Приведите пример задачи Коши, имеющей
решения x и y, которые не связаны ни неравенством
Однако, если заменить в предыдущей теореме произвольное решение x на специально
выбранное, а именно, верхнее, то такая модификация остается справедливой.
Решение xв задачи
| x(t) Ј xв(t), t О [t0, t0 + T] З D(x). |
Аналогично определяется нижнее решение xн
задачи
Задача О2.4. Покажите, что если все решения задачи
Теорема о нестрогих дифференциальных неравенствах.
Пусть непрерывно дифференцируемая на отрезке
| yў(t) Ј f[t, y(t)], t О [t0, t0 + T], | (5) |
| y(t0) Ј x0, | (6) |
а xв — верхнее решение задачи
| y(t) Ј xв(t). | (7) |
Схема д о к а з а т е л ь с т в а этой теоремы такова. Рассмотрим последовательность задач Коши
| xў = fk(t, x), |
| x(t0) = x0, |
где fk(t, x) =
f(t, x) + 1/k
(k О N+).
Можно показать, что при некотором
| yў(t) < fk[t, y(t)], t О [t0, t0 + t], |
в силу теоремы о строгих дифференциальных неравенствах
| y(t) < xk(t), t О (t0, t0 + t]. | (8) |
Оказывается, из последовательности {xk}
можно выделить сходящуюся, причем ее предел обязательно является
верхним решением xв
задачи
Эти теоремы остаются, как легко видеть, верными, если заменить все неравенства на противоположные: "<" на ">" и " Ј" на "і" (во второй теореме при этом, естественно, верхнее решение надо заменить на нижнее).
В приложениях в качестве функции y, как правило, фигурирует модуль гладкой функции, в общем случае дифференцируемым не являющийся. Сформулированные теоремы допускают обобщение на случай негладких функций.
Через
|
|
|
|
Очевидно производные числа Дини (конечные или бесконечные) определены для любой
Задача О2.5. Докажите, что
| D*|j(t)| Ј |D*j(t)|. |
Теорема о нестрогих дифференциальных неравенствах с производными числами.
Пусть непрерывная функция y:
| (9) |
а xв — верхнее решение задачи
Условие (9) в этой теореме можно заменить на условие
| *Dyў(t) Ј f[t, y(t)], t О [t0, t0 + T]. | (10) |
В силу очевидных неравенств
Доказательство сформулированной теоремы лишь деталями отличается от доказательства в случае гладких функций y.
Аналогично формулируется теорема о строгих дифференциальных неравенствах с производными числами.
Помимо верхнего и нижнего решений в
интегральной воронке
задачи Коши (
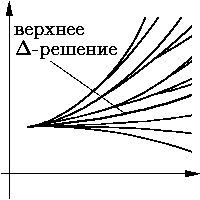
Формально определение, например, верхнего
D-решения выглядит так. Пусть
|
где xнt — нижнее решение
уравнения (1), совпадающее в точке t
с
|
Верхнее D-решение — это наибольшее из решений задачи
Доказательство существования верхнего D-решения и нижнего D*-решения достаточно сложно и мы его опускаем, отсылая читателя к специальной литературе.
Задача О2.6. Приведите пример задачи Коши, у которой верхнее, нижнее, верхнее D- и нижнее D*-решения различны.
Теорема о строгих дифференциальных неравенствах на полуинтервале.
Пусть непрерывно дифференцируемая на
|
yў(t) <
f[t, y(t)], t О
(t0, t0 + T], y(t0) Ј x0. |
Иногда в приложениях бывает удобнее и проще получить оценку типа
| (11) |
нежели оценку типа (5). Из нее также вытекает оценка (7), правда, при дополнительных ограничениях на функцию f. Точнее, имеет место следующая
Теорема о нестрогих интегральных неравенствах. Пусть функция f
является неубывающей по второму аргументу при любом
фиксированном значении первого. Тогда из неравенств (11) и
Доказывается эта теорема очень просто: обозначим правую часть
неравенства (11) через z(t).
Очевидно,
| zў(t) = f[t, y(t)] Ј f[t, x(t)], t О [t0, t0 + T]. |
Утверждение теоремы следует теперь из теоремы о нестрогих дифференциальных неравенствах.
Частным случаем этой теоремы является известная нам
лемма
Аналогично формулируются и доказываются аналоги этой теоремы со
строгими неравенствами, со строгими неравенствами на полуинтервале
В заключение поясним, как утверждения о дифференциальных и
интегральных неравенствах могут быть перенесены на многомерный случай. Будем говорить,
что два вектора
Задача О2.7. Докажите, что если отображение
(t, x) ® f(t, x)
монотонно по x (
Например, теорема о системах строгих дифференциальных
неравенств формулируется так. Пусть непрерывно дифференцируемая функция
|
yў(t) <
f[t, y(t)],
t О
[t0, t0 + T], y(t0) Ј x0, |
Подчеркнем, что в теоремах о системах интегральных неравенств требуется монотонность (а не только внедиагональная монотонность) функции f по x.
Литературные указания. Различные теоремы о дифференциальных и интегральных неравенствах встречаются во многих учебниках и монографиях по теории дифференциальных уравнений (см., напр., [Коддингтон — Левинсон, Хартман, Красносельский]). Монографии [ Мамедов — Аширов — Атдаев, Lakshmikantham — Leela, Rabczuk, Szarski, Walter] (см. также [Беккенбах — Беллман]) практически целиком посвящены неравенствам и их приложениям.
Задачи.
О2.8. Пусть в теореме о строгих дифференциальных неравенствах
неравенство (3) выполнено только при тех t,
для которых
О2.9. Пусть xi: [t0,
t0 + T] ® R
| xў = fi(t, x), x(t0) = x0, |
где непрерывные функции fi:
| x1(t) < x2(t). |
О2.10. Пусть fi:
|
и, кроме того, x1(t0)
Ј y1(t0),
x2(t0) і
y2(t0). Докажите, что при всех
| x1(t) < y1(t), x2(t) > y2(t). |
О2.11. Сформулируйте и докажите аналог утверждения предыдущей задачи с производными числами Дини.
О2.12. Пусть f: [t0,
t0 + T]×R ®
R — непрерывная ограниченная на
всей области определения функция. Докажите, что задача
Коши
О2.13. Пусть xk — решение задачи Коши
|
на отрезке [t0, t0+T]
(k О N+)
и пусть последовательность {xk}
равномерно сходится на этом отрезке к
функции x*. Покажите, что x* —
верхнее решение задачи
О2.14. Пусть все решения скалярной задачи Коши для уравнения
(1)
| yў(t)
Ј f[t, y(t)],
zў(t) Ј
f[t, z(t)], t О
[t0, t0 + T], y(t0) Ј x0, z(t0) Ј x0. |
Пусть g: [t0, t0 + T]×R ® R задается формулой
| g(t, x) = f[t, max{x, y(t), z(t)}]. |
Докажите, что решение задачи Коши
| xў =
g(t, x), t О
[t0, t0 + T], x(t0) = x0 |
существует, удовлетворяет на [t0, t0 + T] неравенствам
| x(t) і y(t), x(t) і z(t) |
и является решением уравнения (1).
О2.15. Пусть f такая же, как и в предыдущей задаче.
Используя компактность множества решений задачи
Коши
О2.16. Покажите, что если x: [a, b]
® R — непрерывная функция и
О2.17. Используя теорему о нестрогих дифференциальных неравенствах с производными числами, докажите теорему о непрерывной зависимости решений от параметра.
О2.18. Пусть f: [t0, t0 +
T]×R ® R
удовлетворяет условиям обобщенной
теоремы
О2.19. Пусть f такая же, как и в
О2.20. Перенесите утверждение предыдущей задачи на системы дифференциальных уравнений.
О2.21. Покажите, что правая часть линейной системы уравнений
| xў = A(t)x + b(t) |
внедиагонально монотонна
в том и только том случае, когда внедиагональные элементы матрицы A(t)
при каждом t неотрицательны:
О2.22. Пусть f: [t0, t0 +
T]×R ® R удовлетворяет
условиям Каратеодори
и x — верхнее
решение Каратеодори на
[t0, t0 + T]
задачи Коши
| yў(t) Ј f[t,y(t)]. |
Тогда, если y(t0) Ј x0, то
| y(t) Ј x(t) |
при всех t О [t0, t0 + T].
О2.23. Перенесите утверждение предыдущей задачи на системы дифференциальных уравнений.
В следующих двух задачах описывается так называемый
метод двусторонних приближений
| (x*)ў(t) > f[t, x*(t)], |
| xў*(t)< f[t, x*(t)] |
при всех t О
[t0, t0 + T].
Определим функции
| g(t, x, y, z) = f(t, z) + fxў(t, z)(x – z), |
|
Определим теперь последовательности функций
{xk} и {yk}
на
| x0 = x*, y0 = x*; |
функция xk+1 есть решение задачи Коши (для линейного дифференциального уравнения)
| xў = G[t, x, xk(t), yk(t)], x(t0) = x0, |
а yk+1 — задачи Коши
| xў = g[t, x, xk(t), yk(t)], x(t0) = x0. |
(Как можно геометрически интерпретировать эти решения?)
О2.24. Докажите, что если x — решение задачи
| yk(t) <
yk + 1(t) <
x(t) < xk+1(t) <
xk(t), xўk(t) > f[t, xk(t)], yўk(t) < f[t, yk(t)]. |
О2.25. Докажите, что
|
File based on translation from
TEX by TTH,
version 2.32.
Created 15 Jan 2000, 12:30.
Last modified 22 Apr 2002.