§ О25. Краевые задачи Штурма — Лиувилля

Рассмотрим уравнение второго порядка

yўў + lr(x)y = 0,   x О [0, l]

(1)

с краевыми условиями

y(0) = 0,   y(l) = 0.

(2)

Здесь мы в отличие от остального изложения принимаем для независимой переменной обозначение x, а не t; соображения, по которым это сделано, станут ясны чуть ниже. В уравнении (1) r — непрерывная положительная на [0, l] функция, а l — скалярный параметр.

Задача об отыскании тех значений l, при которых уравнение (1) имеет ненулевые решения, удовлетворяющие краевым условиям (2), вместе с задачей об отыскании этих решений называется краевой задачей Штурма — Лиувилля или краевой задачей на собственные значения. Здесь мы рассматриваем простейшую из них. Некоторые более общие случаи мы приводим в задачах в конце очерка.

Основным источником задач Штурма — Лиувилля служит так называемый метод Фурье решения уравнений в частных производных. Поясним его суть на простейшем примере уравнения колебаний струны. Представим себе струну, натянутую вдоль оси абсцисс между точками x = 0 и x = l. Обозначим через u(x, t) положение в момент времени t точки струны, которая в положении покоя находилась на оси абсцисс в точке с координатой x (мы предполагаем, что каждая точка струны колеблется только в вертикальном направлении (см. рис. 1). Тогда известно (см., напр., [Кошляков — Глинер — Смирнов, Фихтенгольц]), что функция u удовлетворяет следующему уравнению в частных производных второго порядка

Рис. 1.

¶2u ¶t2 = 1 r(x) · ¶2u ¶x2 ,   x О [0, l], t і 0,

(3)

называемому уравнением свободных колебаний струны. Коэффициент r в нем прямо пропорционален локальной плотности струны и обратно пропорционален ее натяжению; из физических соображений его можно считать положительным. Закрепленность концов струны математически выражается краевыми условиями

u(0, t) = 0, u(l, t) = 0,   t і0.

(4)

Кроме того, для выделения единственного решения уравнения (3) нужно задать так называемые начальные условия — положение и скорость каждой точки струны в начальный момент времени:

u(x,0) = f(x),   ¶u ¶t к к t = 0 = g(x),   x О [0, l].

(5)

Метод Фурье решения начально-краевой задачи (3) – (5) заключается в том, что сначала ищутся частные нетривиальные решения задачи (3) – (5), представимые в виде

u(x, t) = y(x)·t(t),

(6)

а затем решение задачи (3) – (5) ищется в форме рядов, составленных из решений вида (6).

Подстановка (6) в уравнение (3) приводит после несложных преобразований к уравнению

yўў(x) r(x)y(x) = tўў(t) t(t) .

(7)

Поскольку в последнем уравнении левая и правая его части являются функциями различных независимых переменных x и t, то оно удовлетворяется в том и только том случае, если обе части принимают одно и то же постоянное значение; нам удобно обозначить его через -l. Таким образом, уравнение (7) эквивалентно системе линейных дифференциальных уравнений второго порядка

tўў + lt = 0,   t і 0,

(2)

yўў + lr(x)y = 0,   x О [0, l].

(2)

(точнее, уравнение (7) и система (8) – (9) эквивалентны лишь на решениях, не обращающихся в нуль; предоставляем читателю возможность самому произнести все нужные слова).

Уравнение (8) исследуется тривиально — это линейное уравнение с постоянными коэффициентами. Уравнение же (9) вместе с вытекающими из (4) нулевыми краевыми условиями для функции y представляет собой в точности задачу Штурма — Лиувилля (1) – (2).

Прежде чем переходить к основным результатам теории, опишем трактовку краевой задачи Штурма — Лиувилля в операторных терминах. Пусть D(L) — линейное пространство дважды непрерывно дифференцируемых на [0, l] функций, удовлетворяющих краевым условиям (2); мы считаем, что D(L) вложено в C[0, l]. Пусть L — действующий из D(L) в C[0, l] оператор, определенный формулой

(Ly)(x) = – 1 r(x) ·yўў(x).

Тогда, очевидно, если скаляр l₀ и функция y₀ (№ 0) являются решением краевой задачи Штурма — Лиувилля (1) – (2), то l₀ — собственное число, а y₀ — собственный вектор оператора L и наоборот. Поэтому решения (l, y) краевой задачи (1) – (2) часто называют собственными числами (или значениями) и собственными функциями этой задачи, имея в виду собственные числа и собственные векторы ассоциированного с ней оператора L.

Введем в линейном пространстве D(L) билинейную форму

(u, v)D(L) =  т l 0 r(x)u(x)v(x) dx

(в дальнейшем в этом очерке индекс D(L) мы будем опускать).

Задача О25.1. Докажите, что (·,·) — скалярное произведение.

Оказывается, что в пространстве D(L) со скалярным произведением (·,·) оператор L симметричен:

(Ly, z) = (y, Lz)

для любых y, z О D(L), и положителен:

(Ly, y) > 0

при всех y О D(L) > 0.

Задача О25.2. Докажите последние утверждения.

Поэтому многие описываемые ниже утверждения теории краевых задач Штурма — Лиувилля являются следствиями общей теории симметричных положительных операторов, действующих в пространстве со скалярным произведением.

Итак, перейдем к описанию общих свойств собственных чисел и собственных функций задачи Штурма — Лиувилля.

Во-первых, каждому собственному числу отвечает в точности одномерное подпространство собственных функций. Действительно, в противном случае уравнение (1) при данном собственном значении l имело бы по крайней мере два линейно независимых решения, удовлетворяющих краевым условиям (2). Это означало бы, поскольку множество его (уравнения) решений двумерно, что любое решение этого уравнения обращается в нуль на концах промежутка [0, l].

Задача О25.3. Докажите, что последнее утверждение неверно.

Во-вторых, собственные функции, отвечающие различным собственным значениям, ортогональны относительно скалярного произведения (·,·). Действительно, пусть (l₁, y₁) и (l₂, y₂) — решения задачи (1) – (2), т. е. Ly₁ = l₁y₁ и Ly₂ = l₂y₂, причем l₁ № l₂. Тогда

(y1, y2) = 1 l1 (Ly1, y2) = 1 l1 (y1, Ly2) = l2 l1 (y1, y2),

откуда и следует наше утверждение

Задача О25.4. Покажите, что собственные функции, отвечающие различным собственным значениям, линейно независимы.

Задача О25.5. Покажите, что все собственные значения задачи (1) – (2) вещественны.

Более того, легко видеть, что все собственные значения задачи Штурма — Лиувилля положительны. В самом деле, если (l, y) — решение задачи (1) – (2), то

l(y, y) = (Ly, y) > 0,

откуда следует положительность l.

Существенно менее тривиальным является следующее утверждение: множество всех собственных значений задачи Штурма — Лиувилля образуют монотонно возрастающую стремящуюся к бесконечности последовательность: 0 < l₁ < l₂ < ..., < lim_k®Ґl_k = +Ґ. Другими словами, краевая задача Штурма — Лиувилля имеет в точности счетное число собственных значений, причем, единственной точкой сгущения множества собственных значений является точка +Ґ.

Опишем план  д о к а з а т е л ь с т в а. Не теряя общности, можно считать, что функция r продолжена до непрерывной, определенной на [0, +Ґ) функции, причем

0 < r Ј r(x) Ј P < Ґ,    x О [0, Ґ).

Обозначим через y_l решение уравнения (1), определенное на [0, Ґ) и удовлетворяющее начальным условиям

y(0) = 0,   yў(0) = 1.

Функция y_l имеет на [0, Ґ) бесконечное число нулей (докажите!) Пусть z_k(l) (k = 1,2, ...) при каждом фиксированном l О (0, Ґ) — нули функции y_l, занумерованные по возрастанию (см. рис. 2).

Рис. 2.

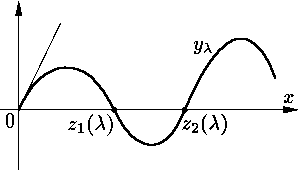
Заметим, что решение yl вместе со своей производной непрерывно зависит от l в топологии равномерной сходимости на каждом конечном промежутке (см. теорему 4.1.3). Далее, т. к. yўl[zk(l)]№ 0 (в противном случае решение yl в точке zk(l) обращалось бы в нуль вместе со своей производной; в силу единственности решения отсюда следовало бы, что yl є 0, что противоречит начальным условиям), по теореме о неявной функции zk(l) непрерывно зависит от l.

Кроме того, сравнивая уравнение (1) при различных l, с помощью теоремы Штурма легко показать, что z_k(l) при каждом k монотонно убывает по l. Сравнение с уравнением

yўў + lry = 0

показывает, что при при каждом k

lim l®Ґ zk(l) = 0,

(10)

а сравнение с уравнением

yўў + lPy = 0

— что

lim l®0 zk(l) = Ґ,

(11)

Обозначим теперь через l_k решение уравнения

zk(l) = l

(k = 1,2, ...). В силу непрерывности zk и соотношений (10), (11) это решение существует, а в силу монотонности zk оно единственно. Очевидно, lk — собственное значение, а ylk — соответствующая собственная функция задачи (1) – (2). Нетрудно видеть также, что других собственных значений нет.

Задача О25.6. Проведите полное доказательство.

Задача О25.7. Найдите собственные значения и собственные функции

yўў + lw2y = 0,

y(0) = 0, y(1) = 0.

Анализ доказательства показывает, что всякая собственная функция, отвечающая собственному значению l_k, имеет на промежутке [0, l] в точности k + 1 нуль.

Задача О25.8. Докажите это утверждение.

Таким образом, каждая задача Штурма — Лиувилля (1) – (2) имеет счетное число собственных значений 0 < l₁ < l₂ < ..., причем каждому собственному значению l_k отвечает ровно одна, определяемая с точностью до постоянного множителя, собственная функция y_k. Удобно считать, что y_k нормированы соотношением

(yk, yk) = т l 0 r(x)y2k(x) dx= 1.

Тогда собственные функции {yk}Ґk=1 образуют ортонормированную систему:

(yk, yl) = dkl,

где d_kl — символ Кронекера.

Вернемся теперь к исследованию уравнения свободных колебаний струны. После того, как собственные значения задачи (1) – (2) найдены, решения уравнения (8) выписываются в явном виде:

t(t) = akcos Ц lk t+ bksin Ц lk t;

здесь a_k и b_k — произвольные постоянные. Поэтому решение вида (6) задачи (3) – (4) выглядит так:

uk(x, t) = ж и akcos Ц lk t+ bksin Ц lk t  ц ш yk(x).

В силу линейности уравнения (3) и однородности краевых условий (4) суммы, составленные из решений такого вида, являются решениями задачи (3) – (4). Более того, если ряд вида

uk(x, t) = Ґ е k = 1 ж и akcos Ц lk t+ bksin Ц lk t  ц ш yk(x)

сходится и его можно дважды дифференцировать почленно по x и t, то его сумма также является решением задачи (3) – (4). Для того, чтобы удовлетворить начальное условие (5) остаются константы a_k и b_k. Очевидно, они должны быть такими, чтобы выполнялись соотношения

Ґ е k = 1 akyk(x) = f(x),    Ґ е k = 1 bk Ц lk yk(x) = g(x).

(12)

Поэтому возникает вопрос о возможности представления произвольной непрерывной функции в виде ряда (12). Оказывается, ортонормальная система собственных функций {yk}Ґk=1задачи Штурма — Лиувилля является базисом в пространстве непрерывных на [0, l] функций (и даже в некотором более широком пространстве), точнее, для любой непрерывной на [0, l] функции f ряд

Ґ е k = 1 akyk(x),

где

ak = т l 0 r(x)f(x)yk(x) dx

сходится к f в следующем интегральном смысле:

т l 0 r(x) к к Ґ е k = 1 akyk(x) – f(x) к к 2 dx ® 0 при m ® Ґ.

Доказательство этого факта выходит за рамки нашей книги.

Литературные указания. Основы теории краевых задач Штурма — Лиувилля описаны, напр., в [Коддингтон — Левинсон, Трикоми, Хартман]. Продвинутое изложение и связи этих задач с функциональным анализом можно найти в [Костюченко — Саргсян, Левитан, Левитан — Саргсян, Марченко, Наймарк, Титчмарш].

Задачи. О25.9. Пусть l₁, l₂, ... — собственные значения задачи (1) – (2). Докажите, что l₁ – a, l₂ – a, ... — собственные значения задачи

yўў + [a + lr(x)]y = 0,

y(0) = 0,    y(l) = 0.

О25.10. Докажите, что собственные значения задачи (1) – (2) получаются из собственных значений задачи

yўў – lr(x)y = 0,

y(0) = 0,    y(l) = 0.

сменой знака.

О25.11. Пусть 0 < l₁ < l₂ < ... — собственные значения задачи (1) – (2), а 0 < m₁ < m₂ < ... — собственные значения задачи

yўў + lr1(x)y = 0,

y(0) = 0,    y(l) = 0

(r₁ непрерывна и положительна на [0, l]). Докажите, что если r(x) Ј r₁(x) при всех x О [0, l], то m_k Ј l_k (k = 1,2, ...).

О25.12. Перенесите результаты очерка на краевую задачу Штурма — Лиувилля вида

yўў + [q(x) + lr(x)]y = 0,

y(0) = 0,    y(l) = 0;

здесь q и r — непрерывные на [0, l] функции, r(x) > 0.

О25.13. Обобщите утверждения очерка на краевую задачу Штурма — Лиувилля вида

d dx [p(x)yў] + [q(x) + lr(x)]y = 0,

(13)

y(0) = 0,   y(l) = 0,

(14)

где p, q и r — непрерывные на [0, l] функции, причем p и r положительны.

О25.14. Докажите, что при увеличении функции q в задаче (13) – (14) (p и r неизменны) собственные значения этой задачи уменьшаются.

О25.15. Докажите, что при увеличении функции r в задаче (13) – (14) (p и q неизменны) положительные собственные значения этой задачи увеличиваются, а отрицательные уменьшаются.

О25.16. Как выглядят результаты очерка для задачи

yўў + lr(x)y = 0,

y(0) = 0,    yў(l) = 0?

О25.17. Обобщите результаты очерка на краевую задачу

d dx [p(x)yў] + [q(x) + lr(x)]y = 0,

y(0)cos j – p(0)yў(0)sin j = 0,

y(l) cosy + p(l)yў(l)sin y = 0,

где p, q и r — непрерывные на [0, l] функции, p(x) > 0, r(x) > 0; j, y — фиксированные константы.

О25.18. Пусть l1, l2, ... — собственные значения задачи (1) – (2). Докажите, что ряд е Ґk=1lk–1 сходится.

О25.19. Докажите, что задача

yўў + lr(x)y = b(x),

y(0) = 0,    y(l) = 0

при l = l_k разрешима в том и только том случае, если

т l 0 b(x)yk(x) dx = 0;

здесь (l_k, y_k) — решение задачи (1) – (2).

О25.20. Рассмотрим задачу Штурма — Лиувилля

d dx [p(x)yў] + ly = 0,

(15)

y(0) = 0,   y(l) = 0

(16)

(p непрерывна и положительна на [0, l]). Пусть G(t, s) — функция Грина задачи (15) – (16) при l = 0. Докажите, что наименьшее собственное значение l₁ задачи (15) – (16) задается формулой

1 l1 = sup м н о т l 0 т l 0 G(x, s)y(s)y(x) ds dx:  y О C[0, l],    т l 0 y2(s) ds = 1 ь э ю .

О25.21. (Продолжение задачи О25.7). Пусть струна однородна, т. е. r(x) є w². Тогда l_k = (kp/wl)². Этим собственным значениям отвечают колебания вида

u(x, t) = sin kpt wl .

В колебаниях струны вида

Ґ е k = 1 aksin kpt wl .

первый член называется основным тоном, а остальные — обертонами. Докажите, что если струну зажать в центре, то частота колебаний всех гармоник удвоится. (Это соответствует повышению высоты звука, издаваемого колеблющейся струной, в точности на октаву.)

О25.22. Пусть в начальный момент времени однородная струна оттянута в точке x = c на высоту h, а затем отпущена с нулевой начальной скоростью. Найдите закон колебаний струны.

О25.23. Пусть отклонение однородной струны в начальный момент времени равно нулю, а колебания струны возбуждаются ударом молоточка, сконструированного так, что начальное распределение скоростей задается соотношением

g(x) = м п н п о cos  p(x – c) h   при  |x – c| Ј   h 2 , 0  при  |x – c| >   h 2 .

Найдите закон колебаний струны.

File based on translation from T_EX by T_TH, version 2.32.
Created 20 Mar 2000, 11:08.
Last modified 30 Apr 2002.