|
§ 1.4. О сходимости явных методов |

|
... Для меня
Краса Отелло — в подвигах Отелло.
В. Шекспир. Отелло
В этом параграфе доказываются общие теоремы об условиях
сходимости явных одношаговых методов. В качестве приложений
рассматриваются явные методы Рунге — Кутты.
Мы часто будем использовать следующее вспомогательное утверждение.
1.4.1. Лемма.
Пусть последовательность
an неотрицательных чисел удовлетворяет
условиям: a0 = 0 и
|
ai Ј (1 + tA)ai-1 + tB, i = 1,2, ...
| (1) |
(A и B — неотрицательные константы). Тогда при ti Ј T
Д о к а з а т е л ь с т в о. (ср. с п. 1.2.10).
По индукции покажем, что при всех i
При i = 0 неравенство (2) очевидно выполнено. Если же оно выполнено при некотором i > 0, то при том же i
| ai+1 Ј (1 + tA)ai + tB Ј (1 + tA) | (1 + tA)i - 1
A |
B + tB = |
|
| = | ж
и |
(1 + tA)i+1 - 1 - tA
A | B + t |
ц
ш | B = |
(1 + tA)i+1 - 1
A | B |
|
и (2) при всех i доказано.
Далее, поскольку 1 + tA Ј 1 + tA + (tA)2/ 2! + ... = etA и ti Ј T,
(1 + tA)i - 1
A | B Ј | eitA - 1
A | B Ј | eAT - 1
A | B, |
|
что и требовалось.
Задача 1.4.1. Докажите, что если a > 0, то из неравенства (1) вытекает неравенство
при it Ј T.
В заключение отметим, что данная лемма является разностным
аналогом классической леммы Гронуолла о дифференциальных неравенствах.
1.4.2. Явные одношаговые методы.
Явные методы Рунге — Кутты относятся к так называемым явным одношаговым методам: для того, чтобы вычислить значение сеточного решения в точке ti необходимо знать его значение только в предшествующей точке ti-1. Разностный
оператор общего явного одношагового метода имеет вид
| (Ftx)i = | м
п
н
п
о |
xi - xi-1
t | - F(ti-1, xi-1, t), если i = 1, ..., n, |
|
x0, если i = 0
|
|
| (3) |
(здесь F: R×Rm×[0, +Ґ) ® Rm). Разностную схему (S) метода мы, как обычно, будем записывать в виде рекуррентного соотношения
|
xi = xi-1 + tF(ti-1, xi-1, t), | (4) |
опуская начальное условие x0 = x0, которое мы считаем выполненным по умолчанию. Функция F часто называется инкрементом,
или приращением метода.
Задача 1.4.2. Каков инкремент явного метода Эйлера и метода предиктор-корректор?
Всегда будем предполагать, что
инкремент метода есть непрерывная по совокупности переменных
и удовлетворяющая при достаточно малых t
условию Липшица по второму аргументу с (универсальной) константой L функция. |
|
1.4.3. Теорема (необходимое условие сходимости явных одношаговых методов).
Если явный одношаговый метод сходится, то F(t, x, 0) є f(t, x) при всех (t, x) О R×Rm.
Д о к а з а т е л ь с т в о. Предположим противное: в
некоторой точке (t0, x0) О R×Rm
|
F(t0, x0, 0) № f(t0, x0). |
В силу теоремы Коши — Пикара начальная задача
имеет единственное решение, скажем y (определенное на всей оси, поскольку F удовлетворяет условию Липшица по x). Через j, как обычно,
обозначается решение задачи (E) – (C).
Пусть теперь jt — решение разностной схемы (S) с определенным формулой (3) разностным оператором, т. е.
(см. (4))
|
(jt)i = (jt)i-1 + tF[ti-1, (jt)i-1, t].
| (7) |
По условию теоремы
|
||jt - Ptj||t ® 0 при t ® 0.
| (8) |
Если мы докажем, что
|
||jt - Pty||t ® 0 при t ® 0.
| (9) |
то тогда из (8) и (9) будет вытекать, что
В самом деле, соотношения (8) и (9)
означают, что функции j и y равномерно аппроксимируются в узлах сетки одной и той же сеточной функцией jt, а поскольку j и y непрерывны на [t0, t0 + T] и шаг сетки стремится к нулю, имеет место (10).
Задача 1.4.3. Проведите подробные рассуждения.
Но тогда, в частности, j(t0) = y(t0), а
следовательно,
|
jў(t0) = f[t0, j(t0)] = f(t0, x0) № F(t0, x0, 0) = F[t0, y(t0), 0] = yў(t0), |
что противоречит (10).
Осталось доказать соотношение (9). Положим
или, что то же,
|
y(ti) = y(ti-1) + tri.
| (11) |
По теореме о среднем (см. любой курс математического анализа)
|
ri = yў(ti-1 + qi t) = F[ti-1 +qit, y(ti-1 + qit)], | (12) |
где qi О (0, 1). Обозначим (jt)i - y(ti) через ei. В этих обозначениях из (7) и (11) следует, что
|
ei = ei-1 +t(F[ti-1,(jt)i-1, t] - ri). |
Добавляя и отнимая необходимые слагаемые и используя (12), получаем следующую оценку
||ei|| Ј ||ei-1|| + t||F[ti-1, (jt)i-1, t] - F[ti-1, y(ti-1), t]|| +
+ t||F[ti-1, y(ti-1), t] - F[ti-1, y(ti-1), 0]|| +
+ t||F[ti-1, y(ti-1), 0] - F[ti-1 + qit, y(ti-1 + qit), 0]||. | |
(13) |
Обозначим сумму двух последних слагаемых в правой части (13) через t[r(t)]i. Очевидно, [r(t)]i ® 0 при t ® 0 равномерно по i О {1, ..., n}, так как F и y непрерывны (и, следовательно, равномерно непрерывны на компактах).
Задача 1.4.4. Докажите последнее утверждение.
Второе слагаемое в правой части оценивается с помощью условия
Липшица величиной tL||(jt)i-1 - y(ti-1)|| = tL||ei-1||.
Тогда, продолжая (13), получаем
|
||ei|| Ј (1 + tL)||ei-1|| + t||r(t)||t. |
По лемме 1.4.1 ||ei|| Ј r(t)(eLT - 1)/L и соотношение (9), а вместе с
ним и теорема доказаны.
Задача 1.4.5. Докажите, что явная схема Эйлера и схема предиктор-корректор удовлетворяют условиям теоремы 1.4.3.
1.4.4. Теорема (достаточное условие сходимости явных одношаговых методов).
Условие F(t, x, 0) є f(t, x) при всех t О R×Rm является и достаточным условием для сходимости метода (4).
Д о к а з а т е л ь с т в о теоремы, по-существу, нами уже проведено: в силу теоремы Коши — Пикара решение j задачи (E) – (C) и решение y задачи (5) – (6) единственны и поэтому j = y, а следовательно, доказанное выше соотношение (9)
равносильно нужному соотношению (8).
1.4.5. Сходимость схем Рунге — Кутты.
Поскольку для произвольной явной p-этапной схемы Рунге — Кутты (см. (1.3.10) – (1.3.12))
в силу доказанных теорем 1.4.3 и 1.4.4 для сходимости этих схем необходимо и достаточно, чтобы
Как уже говорилось выше, на практике гораздо более полезной оказывается информация о порядке сходимости схемы.
1.4.6. О порядке сходимости явных одношаговых схем.
Определим на R×Rm×[0, +Ґ) функцию r, положив для
произвольных t0 О R, x0 О Rm и t і 0
| r(t0, x0, t) = | м
п
н
п
о | | f(t0, x0), если t = 0, | | | j(t0 + t) - j(t0)
t | , если t > 0, |
|
|
|
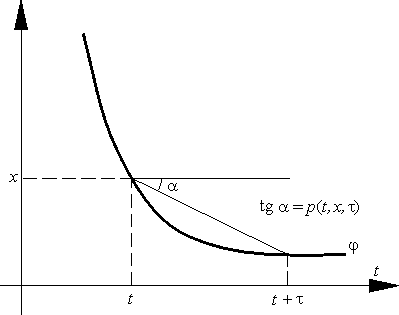
Рис. 4.
где j — решение задачи (E) – (C) (рис. 4). Очевидно, при t > 0
|
j(t0 + t) = j(t0) +tr(t0, x0, t). | (14) |
Другими словами, явный одношаговый метод с инкрементом r является идеальным, т. е. точным на каждом шаге.
Теорема о порядке сходимости явных одношаговых схем. Пусть для некоторых k > 0 и M і 0
при всех (t, x) О R×Rm и достаточно малых t. Тогда явный одношаговый метод (4) сходится с k-м порядком, точнее, имеет место оценка
| ||jt - Ptj||t Ј | eLT - 1
L |
Mtk.
|
| (16) |
Суть этой теоремы другими словами можно выразить так: если инкремент метода (4) отличается от инкремента идеального метода на величину порядка O(tk), то метод
сходится с k-м порядком.
Д о к а з а т е л ь с т в о. Обозначим, погрешность (jt)i - j(ti) метода в точке ti на решении j через ei.
Имеем (см. (4) и (14))
||ei|| = ||ei-1 + t(F[ti-1, (jt)i-1, t] - r[ti-1, j(ti-1), t])|| Ј
Ј ||ei-1|| + t||F[ti-1, (jt)i-1, t] - F[ti-1, j(ti-1), t]|| +
+ t||F[ti-1, j(ti-1), t] - r[ti-1, j(ti-1), t]|| Ј
Ј ||ei-1|| + tL|| (jt)i-1 - j(ti-1)|| +Mtk+1 Ј (1 + tL)||ei-1|| + tMtk+1. |
Применяя к последовательности ai = ||ei|| лемму 1.4.1, получаем неравенство
| ||ei|| Ј | eLT - 1
L |
Mtk при it Ј T,
|
|
которое, очевидно, эквивалентно нужному нам неравенству (16).
1.4.7. Пример. Сходимость метода предиктор-корректор.
Теорема 1.4.6 позволяет устанавливать сходимость явных методов Рунге — Кутты и, более того, позволяет получать полезные на практике оценки близости между точным и сеточным решениями.
Рассмотрим, например, метод предиктор-корректор. Для простоты будем считать уравнение (E) скалярным. Для того чтобы воспользоваться оценкой (16), нам нужны оценки константы Липшица L инкремента метода F по
второму аргументу и константы M в неравенстве
(15). Начнем с более простой оценки константы L. Для метода предиктор-корректор (см. задачу 1.4.2)
| F(t, x, t) = | 1
2 | (f(t, x) + f[t + t, x + tf(t, x)]). |
|
Тогда (напомним, что L — константа Липшица функции f по x)
| ||F(t, x, t) - F(t, y, t)|| Ј | 1
2 | ||f(t, x) - f(t, y)|| + |
|
| + | 1
2 | ||f[t + t, x + tf(t, x)] - f[t + t, y + tf(t, y)]|| Ј |
|
| Ј | L
2 |
||x - y|| + |
L
2 | ||x + tf(t, x) - y - tf(t, y)|| Ј | L
2 | ||x - y|| + |
|
| + | L
2 | (||x - y|| + t||f(t, x) - f(t, y)||) Ј L | ж
и | 1 + |
L
2 | ц
ш |
||x - y||. |
|
Поэтому
Оценка константы M получается более громоздко. Пусть функция f дважды непрерывно дифференцируема и, кроме того, все частные производные от нулевого до второго порядков ограничены (скажем, константой M). Тогда, во-первых (напомним, что мы опускаем аргумент (t, x) у функции f и ее производных), раскладывая F в ряд Тейлора по степеням t,
| F(t, x, t) = F(t, x, 0) + tFўt(t, x,0)+ | t2
2 |
Fўўtt(t, x, qt) = |
|
| = | 1
2 | f + | 1
2 | f + | t
2 | ft + |
t
2 | fx f + | 1
2 |
· | t
2 |
[fttq+ 2ftxqf q + fxxq(f q)2] = |
|
| = f + | t
2 | (ft + fx f ) + | t2
4 | M1(q). |
|
где верхний индекс q означает, что аргумент,
соответствующей функции равен (t + qt, x + qtf(t, x)) (0 < q < 1), а обозначение M1(q) очевидно. Во-вторых (здесь j — решение уравнения (E), проходящее через точку (t, x), т. е. такое, что j(t) = x),
= | | x + tjў(t) + | t2
2 | jўў(t) + | t3
6 | jўўў(t + xt) - x |
t |
= |
|
| = jў(t) + | t
2 | jўў(t) + | t2
6 | jўўў(t + xt) = |
|
| = f + | t
2 | (ft + fx f ) + | t2
6 | (fttx+ 2ftxxf x + fxxx(f x)2+ fxxftx + (fxx)2f x) = |
|
| = f + | t
2 | (ft + fx f ) + | t2
6 | M2(x), |
|
где 0 < x < 1. Поэтому
Поскольку все частные производные функции f до второго порядка ограничены константой M,
|
||M1(q)|| Ј M + 2M2 + M3, |
а
|
||M2(x)|| Ј M + 2M2 + M3 + M2 +M3 = M + 3M2 + 2M3. |
Поэтому
и следовательно,
1.4.8. Замечания.
а) Условие ограниченности производных
функции f можно ослабить до требования их ограниченности
только на некотором множестве, о котором a priori
известно, что в нем лежит искомое решение. В частности, если это
множество замкнуто и ограничено, то достаточно требовать
непрерывности соответствующих производных.
б) Полученная оценка
погрешности, поскольку она расчитана на широкий класс функций,
разумеется, на конкретных задачах выполняется с запасом. Часто на
конкретных задачах полученная фактическая погрешность в десятки
раз ниже теоретической.