
|
§ 1.2 Разностные схемы. Сходимость, аппроксимация,
устойчивость |

|
После такой подготовки приступит он к судебным делам и
прежде всего установит, какого рода эти дела.
Цицерон. Оратор
В данном параграфе на примере явного метода Эйлера даются основные
понятия теории разностных схем — понятия сходимости,
аппроксимации и устойчивости. Доказывается теорема Лакса.
Описываются основные приемы построения разностных схем.
1.2.1. Метод ломаных Эйлера.
Напомним, что метод ломаных Эйлера – это метод нахождения аппроксимирующей интегральную кривую ломаной, который
в образах парка со стрелками-указателями может быть представлен
так (рис. 2). Из точки (t0, x0) = (t0, x0) расширенного фазового пространства движемся
t "секунд", сообразуясь со стрелкой, помещенной в
этой точке, и не обращая внимания на остальные стрелки. Придя (через время
t) в точку (t1, x1), меняем направление, пользуясь указанием, задаваемым стрелкой в точке (t1, x1); через t секунд приходим в точку (t2, x2), опять меняем направление и т. д. Полученная траектория и является ломаной Эйлера, аппроксимирующей решение задачи (E) – (C).
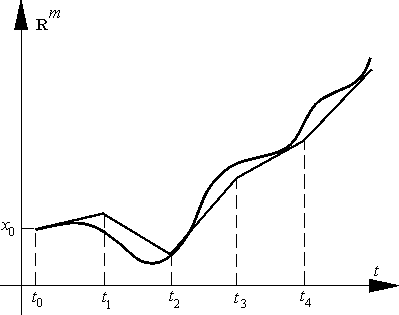
Рис. 2.
Легко видеть, что координаты i-й вершины (i = 1,..., n) ломаной Эйлера определяются формулами
|
ti = t0 + it, x0 = x0,
xi = xi-1 + tf(ti-1, xi-1). | (1) |
Перепишем эти равенства в следующем виде:
xi - xi-1
t |
- f(ti-1, xi-1) = 0, если i = 1,..., n, |
|
1.2.2. Операторная запись задачи (E) – (C).
Запишем метод ломаных Эйлера в общем виде, в
котором могут быть записаны другие разностные методы и который
позволяет укладывать исследование таких методов в общую схему. Для
этого сначала запишем задачу (E) – (C) в операторной
форме. Начальное условие (C) можно записать в виде
где функция g имеет вид g(x) = x(t0) - x0. Тогда начальную задачу (E) – (C) можно записать в операторной форме
где F(x) = (xў(·) - f(·, x), g(x)). Не будем обсуждать подробно вопрос об областях определения и
значений оператора F. В случае задачи (E) – (C)
можно считать, например, что областью определения D(F) оператора F служит пространство C1([t0, t0 + T], Rm) непрерывно
дифференцируемых на отрезке [t0, t0 + T] функций со значениями в Rm, а областью значений R(F) — декартово произведение C1([t0, t0 + T], Rm)×Rm. Заметим, что решение j задачи (E) – (C) есть прообраз нуля для оператора F: j = F-1(0).
1.2.3. Операторная форма метода ломаных Эйлера.
Пусть x — сеточная функция из St. Определим на St оператор Ft равенством
| [Ft(x)]i = |
м
п
н
п
о |
xi –
xi–1
t |
– f(ti–1,
xi–1), если i = 1, ..., n, |
| | xi –
x0, если i = 0; |
|
|
(2) |
(Здесь [Ft(x)]i обозначает значение сеточной функции [Ft(x)] в точке
ti.)
Задача о нахождении ломаной Эйлера, очевидно, эквивалентна задаче о
нахождении решения jt уравнения
|
в пространстве St сеточных функций в следующем смысле: значения (jt)i решения
уравнения (S) в узлах сетки и только они являются
ординатами вершин ломаной Эйлера в точках ti (см. формулу (1)). Таким образом, вместо точного решения j = F-1(0) мы ищем приближенное решение jt = Ft–1(0).
|
1.2.4. Разностные схемы.
Любое уравнение вида (S)
для нахождения сеточной функции x будем называть разностной схемой, а его (уравнения) решение, которое мы всегда будем обозначать jt, — разностным или сеточным решением (уравнения (S)). Оператор Ft будем называть разностным оператором.
Разумеется, в таком общем виде определение разностной схемы никак не связано с исходной задачей Коши (E) – (C) (уравнением (O)). В то же время, если в (S) оператор Ft определен формулой (2), то
разностная схема (S) имеет к задаче (E) – (C) самое
непосредственное отношение (объяснить, что означают эти слова, и
есть цель остальной части параграфа).
В последнем случае разностная схема (S) называется явной (разностной) схемой Эйлера. Явной она называется потому, что ее решение может быть выписано в явном виде с помощью рекуррентных
соотношений:
|
(jt)i = (jt)i-1 +tf[ti-1,(jt)i-1], i = 1, ..., n. |
Единственное отличие метода ломаных Эйлера от явной схемы Эйлера заключается в том, что в первом ищется функция, заданная на отрезке
[t0, t0 + T] (ломаная Эйлера), а во втором — на сетке Gt (вершины этой ломаной).
Задача 1.2.1. Докажите, что разностное решение jt явной схемы Эйлера для задачи Коши
(a О R) на равномерной сетке (ti = it) задается формулой (jt)i = x0(1 + ta)i.
1.2.5. Пример. Сходимость явной разностной схемы Эйлера.
В условиях задачи 1.2.1 разностное решение jt аппроксимирует решение j(t) = x0eat интересующей нас исходной (дифференциальной) задачи в следующем смысле: при всех t О [0, T]
|
(jt)i® x0eat при t® 0,
| (3) |
где i = [t/t] (здесь [t/t] — целая часть числа t/t; ниже мы наряду с обозначением [a] для целой части числа a используем обозначение {a} для его дробной части: a = [a]+ {a}). Действительно,
lim
t®0 |
(jt)i = |
lim
t®0 |
x0(1 + ta)i = x0·
|
lim
t®0 |
(1 + ta)[t/t] =
|
|
= x0·
|
lim
t®0 |
(1 + ta)t/t-{t/t} =
|
|
= x0·
|
lim
t®0 |
(1 + ta)t/t·
|
lim
t®0 |
(1 + ta)-{t/t}.
|
|
Сомножитель limt®0(1 + ta)-{t/t} равен единице, поскольку {t/t} О (0, 1). Второй сомножитель также вычисляется
тривиально:
lim
t®0 |
(1 + ta)t/t =
|
lim
t®0 |
(1 + ta)[1/(ta)] ·at =
|
й
л |
lim
t®0 |
(1 + ta)1/ta
|
щ
ы |
at
|
= eat
|
|
и соотношение (3) доказано.
Задача 1.2.2. Докажите более сильное, чем (3) утверждение
|
||jt - Ptj||t® 0 при t® 0.
|
означающее, что предельное соотношение (3) выполнено равномерно по i О {1, ..., n).
1.2.6. Сходимость разностных схем.
Будем говорить, что разностная схема (S) сходится (к решению j задачи (E) – (C)), если
|
||jt - Ptj||t® 0 при t® 0.
| (4) |
Сходимость разностной схемы означает, что при достаточно малом t значения сеточного (приближенного) решения jt и точного решения j мало отличаются. Соотношение (4) на практике оказывается мало полезным, поскольку на основании его нельзя судить о том насколько малым мы должны выбрать шаг t, чтобы в узлах сетки точное и приближенное решения отличались друг от
друга не более, чем на e (заранее заданную
точность). Если удается доказать, что при достаточно малых t > 0
где C — не зависящая от t константа, то говорят, что схема (S) сходится с порядком k (или является схемой k-го порядка (сходимости)). Оценка (5), если в ней известна (для конкретной задачи (E) – (C)) константа C, позволяет по заранее выбранной точности e a priori выбрать шаг так, чтобы приближенное решение аппроксимировало решение данной (дифференциальной) задачи Коши с точностью e:
|
достаточно взять t Ј kЦe/C.
|
1.2.7 Аппроксимация.
Явная схема Эйлера обладает двумя важными свойствами, из которых, как будет показано ниже, последует ее сходимость с первым порядком. Во-первых, при достаточно малых t
где Ca — константа, не зависящая от t, а j — как обычно, точное решение задачи (E) – (C). В этом случае говорят, что схема (S) имеет
первый порядок аппроксимации на решении. (Если в правой части неравенства (6) стоит Catk, то, соответственно, говорят о схеме k-го порядка аппроксимации (на решении).) Другими словами, неравенство (6) эквивалентно тому, что ||Ft(Ptj)||t = O(t) (в случае схемы
k-го порядка аппроксимации — O(tk)). Тот факт, что разностная схема обладает аппроксимацией на решении, означает, грубо говоря, что при подстановке точного решения дифференциальной задачи в разностную схему мы получаем невязку соответствующего порядка малости по t. (Было бы идеально, если бы после такой подстановки мы получали в левой части нуль, однако в общем случае конструктивно такие схемы выписать нельзя.)
Часто вместо свойства аппроксимации на решении рассматривают формально более жесткое требование, которое называют свойством аппроксимации (в зарубежной литературе — согласованностью); именно, говорят, что схема (S) является схемой k-го порядка аппроксимации на функции x, если при достаточно малых t
Обычно требуется, чтобы схема обладала свойством аппроксимации на множестве функций из некоторого класса гладкости. Очевидно, если решения дифференциального уравнения (E) m раз непрерывно дифференцируемы, а разностная схема обладает k-м порядком аппроксимации (согласованности) на m раз непрерывно дифференцируемых функциях, то она обладает k-м порядком
аппроксимации на решении.
1.2.8. Аппроксимация явной схемы Эйлера.
Покажем, что если функция f в (E)
непрерывно дифференцируема по t и x, то явная схема Эйлера имеет первый порядок аппроксимации на решении. Действительно, пусть j — решение задачи (E) – (C):
|
jў(t) є f[t, j(t)], t О [t0, t0 + T]. |
Поскольку f дифференцируема по t и x, решение j дважды непрерывно дифференцируемо (см.
утверждение о гладкости решений). В частности, найдется M такое, что ||jўў(t)|| Ј M при всех t О [t0, t0 + T]. Кроме того, в силу гладкости j для любых t = 1, ..., n
| j(ti) = j(ti-1 + t) = j(ti-1) +tjў(ti-1) + |
t2
2 |
jўў(ti-1 + Jit), |
|
где J О (0, 1). Но тогда
| [Ft(Ptj)]i = |
(Ptj)i - (Ptj)i-1
t |
- f[ti-1, (Ptj)i-1] = |
|
| = |
j(ti) - j(ti-1)
j |
- f[ti-1, j(ti-1)] = |
|
= |
| j(ti-1) + tjў(ti-1) + | t2
2 |
jўў(ti-1 + Jit) - j(ti-1) |
t
|
– |
|
| - f[ti-1, j(ti-1)] = jў(ti-1) + |
t2
2 |
jўў(ti-1 + Jit) - f[ti-1, j(ti-1)] = |
|
(Если i = 0, то очевидно, [Ft(Ptj)]i = 0.) Из сказанного следует, что
| ||Ft(Ptj)|| t = |
max
0ЈiЈn |
||[Ft(Ptj)]i|| Ј |
|
| Ј |
t
2 |
max
0ЈiЈn |
||jўў(ti-1+Jit)|| Ј t |
M
2 |
= Cat.
|
|
Задача 1.2.3. Покажите, что явная схема Эйлера обладает первым порядком аппроксимации (согласованности) на любой дважды непрерывно дифференцируемой функциию
1.2.9. Устойчивость.
Второе важное свойство, которым обладает явная схема Эйлера, называется устойчивостью и определяется так: если z О St и, кроме того, ||z||t и t достаточно малы, то уравнение
однозначно разрешимо и существует такая не зависящая от t и ||z||t константа Cs, что
|
||y - jt||t = ||Ft-1(z)- jt||t Ј Cs||z||t. | (8) |
|
Устойчивость разностной схемы означает, что малые возмущения z в начальных данных и правой части разностной схемы приводят к равномерно малому по t изменению решения (напомним, что jt — решение невозмущенной системы, а Ft-1(z) — возмущенной). Поскольку jt = Ft-1(z),неравенство
(8), переписанное в виде ||Ft-1(z)- Ft-1(0)||t Ј Cs||z|| t,
означает, в частности, непрерывность обратного к разностному
оператору оператора Ft-1в нуле.
|
|
Устойчивость — очень важное в приложениях свойство разностных схем. При практической реализации на ЭВМ разностных методов возникают, в частности, проблемы, связанные с невозможностью представления точных чисел в компьютере. В результате мы решаем не разностную схему (S), а несколько отличающееся от (S) уравнение. Все такие возмущения в разностной схеме, грубо говоря, можно "перенести в правую часть" и, таким образом, считать, что в ЭВМ ищется решение не разностной схемы (S), но решение возмущенного уравнения (7). Свойство
устойчивости разностной схемы гарантирует близость при достаточно малых t между точным (теоретическим) решением jt разностной схемы и его
практической реализацией Ft-1(z)(где z — суммарный вектор возмущений). Источником возмущений служит не только невозможность точного представления данных в ЭВМ, но и неточность определения физических параметров модели, погрешность
измерений и т.п. |
1.2.10. Пример. Устойчивость явной схемы Эйлера.
Докажем, что явная схема Эйлера устойчива.
|
Разрешимость уравнения (7) для любых t и z очевидным образом следует из того, что явная схема Эйлера
является явной: значения yi решения y = Ft-1(z) этого уравнения определяются рекуррентными формулами |
|
yi = yi-1 + tf(ti-1, yi-1) + tzi, i = 1, ..., n. |
Обозначим y - jt через x. Очевидно,
|
xi = xi-1 + tf(ti-1, yi-1) - tf[ti-1,(jt)i-1] + tzi, i = 1, ..., n. |
Покажем теперь, что
||xi|| Ј (1 + tL)i·
| L + 1
L |
||z||t. |
|
Для этого заметим сначала, что
|
||xi|| = ||xi-1 + tf(ti-1, yi-1) - tf[ti-1,(jt)i-1] + tzi|| Ј |
|
Ј ||xi-1|| + t||f(ti-1, yi-1) -f[ti-1,(jt)i-1]|| + t||zi|| Ј |
|
Ј ||xi-1|| + tL||yi-1 - (jt)i-1|| + t||z|| t = (1 + tL)||xi-1|| + t||z|| t. |
Проведя такие оценки i раз, получим
|
||xi|| Ј (1 + tL)||xi-1|| + t||z|| t Ј |
|
Ј (1 + tL)[(1 + tL)||xi-2|| +t||z|| t] + t||z|| t = |
|
= (1 + tL)2||xi-2|| + [(1 + tL) + 1]t||z|| t Ј ... |
|
... Ј (1 +tL)i|| x0|| + [(1 + tL)i-1 + ... + (1 + tL) + 1]t||z|| t = |
= (1 + tL)i|| x0|| +
|
(1 + tL)i - 1
(1 + tL) - 1 |
t||z||t Ј
|
|
Ј (1 + tL)i|| z|| t +
|
(1 + tL)i- 1
L |
||z|| t = |
|
| = |
(1 + tL)iL + (1+ tL)i - 1
L |
||z||t Ј (1+tL)i·
|
L + 1
L |
||z||t.
|
|
Воспользуемся теперь известным неравенством (1 + a)1/a < e (напомним также, что t = T/n):
|
(1 + tL)i Ј (1 + tL)n = (1 + tL)[(TL)/(tL)] Ј [(1 + tL)[ 1/(tL)]]TL < eTL. |
Окончательно,
||Ft-1z- jt|| t = ||y - jt|| t = ||x|| t =
|
max
0ЈiЈn |
||xi|| Ј |
|
| Ј |
max
0ЈiЈn |
eTL·
|
L + 1
L |
||z|| t = eTL·
|
L + 1
L |
||z||t = Cs|| z|| t.
|
|
Итак, явная схема Эйлера устойчива.
Покажем теперь, что из аппроксимации и устойчивости следует сходимость разностной схемы.
1.2.11. Теорема Лакса.
Любая устойчивая разностная
схема k-го порядка аппроксимации на решении является схемой k-го порядка сходимости.
|
Д о к а з а т е л ь с т в о. Действительно, если разностная схема имеет k-й порядок аппроксимации на решении, то ||Ft(Ptj)||t Ј Catk и поэтому, в частности, при малых t
мала и ||Ft(Ptj)||t. Следовательно, в силу устойчивости,
Ft-1[Ft(Ptj)] существует и ||Ft-1[Ft(Ptj)]- jt||t Ј Cs||Ft(Ptj)||t. Но тогда, очевидно, |
|
||Ptj- jt|| t = ||Ft-1[Ft(Ptj)]- jt||t Ј |
|
Ј Cs|| Ft(Ptj)|| t Ј CsCat = Ctk. |
что и требовалось доказать.
Эта теорема описывает наиболее распространенный способ доказательства сходимости разностных схем.
Задача 1.2.4. Приведите пример не сходящейся разностной схемы, обладающей своством аппроксимации.
1.2.12. Немного о методах построения разностных схем.
Явная схема Эйлера может быть построена, исходя из различных соображений. Каждый из описываемых ниже приемов порождает ряд обобщений явной схемы Эйлера и может иллюстрировать основные методы построения разностных схем. В дальнейшем эти методы будут рассматриваться подробнее.
Попытаемся, отталкиваясь от уравнения (E),
заменить его приближенным в том или ином смысле уравнением так, чтобы в результате получилась разностная схема. Первая идея выглядит так. Заменим в уравнении
производную xў(t) в точке ti-1 ее приближенным значением [x(ti) - x(ti-1]/t, а правую часть — ее значением в этой точке. В результате получим приближенное уравнение
x(ti) - x(ti-1)
t |
» f[ti-1, x(ti-1)] |
|
для отыскания значений точного решения уравнения (E) в точках сетки Gt. Переход к сеточным функциям и замена приближенного равенства точным приводит к точному уравнению для приближенных значений решения, а именно, к явной схеме Эйлера. Использование других аппроксимаций производной в (9) (например, xў(ti-1) » [x(ti+1) - x(ti-1)]/2t, а также других аппроксимаций правой части (например, f[ti, x(ti)]) взамен f[ti-1, x(ti-1)] позволяет получать другие разностные схемы.
Вторая идея основывается на замене дифференциального уравнения (9) интегральным
| x(t + t) = x(t) + | т |
t+t
t | f[s, x(s)]ds, |
| (10) |
Если заменить в (10) t на ti-1, а интеграл — приближенной квадратурной формулой (в данном случае прямоугольников), то мы получим приближенное уравнение
|
x(ti) » x(ti-1) + tf[ti-1, x(ti-1)], |
которое так же, как и выше приводит к явной схеме Эйлера. Если использовать другие квадратурные формулы (заменяя, например,
интеграл на tf[ti, x(ti)] или t[f(ti-1, x(ti-1)) + f(ti, x(ti))]/2), то будут получаться другие разностные схемы.
Третья возможность построения разностных схем связана с разложением решения в ряд Тейлора:
| x(ti) = x(ti-1) + txў(ti-1) + |
t2
2 |
xўў(ti-1) + ... . |
|
"Обрежем" этот ряд до второго члена и выразим производную
xў(ti-1) из (9). В результате получим все то
же приближенное уравнение
|
x(ti) » x(ti-1) + tf[ti-1, x(ti-1)], |
приводящее к явной схеме Эйлера. Удлинение отрезка ряда и другие аппроксимации коэффициентов приводят к другим разностным схемам.
Наконец, четвертая возможность связана с поиском решения в виде
полинома. Допустим, мы ищем решение в виде полинома первого порядка:
|
y(t) = xi-1 + a·(t - ti-1) |
с неизвестным коэффициентом a. Потребуем, чтобы этот полином точно удовлетворял уравнению (9) в некоторой точке ti-1 + a:
|
yў(ti-1 + a) = a = f(ti-1 +a, xi-1 + aa). |
Переходя к сеточным функциям, как и выше, получаем разностную схему:
|
xi = y(ti) = y(ti-1 + t) = xi-1 + tf(ti-1 + a, xi-1 + aa). |
При a = 0 это явная схема Эйлера. Если выбирать отличные от нуля a, а также брать полиномы более высоких порядков, то получается класс различных разностных схем.




