


| § 1.6. Многошаговые методы | 
|
В том и состоит главная польза и лучший плод знакомства с событиями минувшего, что видишь всякого рода поучительные примеры в обрамлении величественного целого.
Тит Ливий. История Рима от основания Города
В этом параграфе описывается класс многошаговых методов.
1.6.1. Одношаговые и многошаговые методы.
Как уже говорилось, все рассмотренные выше методы являлись одношаговыми: для нахождения значения
Итак, допустим к настоящему моменту мы вычислили значения
|
| (1) |
Не известную нам подынтегральную функцию
|
Таким образом, мы приходим к так называемому явному p-шаговому методу Адамса
| (2) |
в котором P — интерполяционный полином, построенный по узлам
Разумеется, (2) представляет собой лишь "заготовку" для метода. Конкретные методы получаются после вычисления коэффициентов интерполяционного полинома и интеграла.
Задача 1.6.1. Покажите, что явный одношаговый метод Адамса есть явный метод Эйлера
1.6.3. Пример: явный двухшаговый метод Адамса.
Интерполяционный полином P (в форме Лагранжа) в случае
|
Тогда, после несложных вычислений, учитывая, что
|
Таким образом, явный двухшаговый метод Адамса имеет вид
| (3) |
Задача 1.6.2. Выведите явный трехшаговый метод Адамса
Обратим внимание на новое обстоятельство. Формула (3)
неприменима при
Заметим, что при выводе явных методов Адамса мы использовали значения интерполяционного полинома P на отрезке
| (4) |
где Q — интерполяционный полином, построенный по узлам
Задача 1.6.3. Покажите, что в случае p = 0 получается неявный метод Эйлера.
Задача 1.6.4. Выведите неявные двух- и трехшаговые методы Адамса.
Явные методы Адамса часто называют методами
1.6.5. Линейные многошаговые методы.
Описанные выше методы укладываются в следующую общую конструкцию. Метод
| (5) |
называется линейным p-шаговым методом. Например, при
Методы (5) называются линейными, потому что в левой части стоит линейный оператор. Если
1.6.6. Проблема "запуска" многошаговых методов.
Как уже отмечалось, формулы (2) так же, как и (4), (5), не являются разностными схемами (вернее, являются неполными разностными схемами), поскольку в них не заданы формулы (уравнения) для вычисления p начальных значений. Здесь нельзя просто положить, например,
1.6.7. Сходимость многошаговых методов.
Без описания процесса запуска многошагового метода мы не можем воспользоваться определениями
| ||(jt)i - (Ptj)i|| Ј C0tk, i = 0, ..., p - 1, |
выполнено неравенство
| ||jt - Ptj|| t Ј Ctk. |
Другими словами, многошаговый метод сходится с k-м порядком, если, будучи запущенным из начальных значений, вычисленных с k-м порядком точности, он дает приближенное решение с k-м порядком точности.
1.6.8. Аппроксимация многошаговых методов.
При определении порядка аппроксимации многошаговых методов можно,
как в
| e(t, x, t) = j(t + pt) - (jt)p, |
где j — решение уравнения (E), проходящее через точку (t, x), а
| (jt)0 = j(t), (jt)1 = j(t + t), ..., (jt)p-1 = j[t + (p - 1)t] | (6) |
(рис. 8).
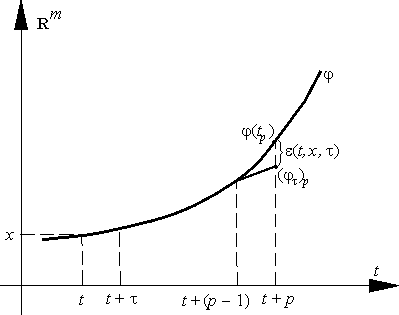
Говорят, что метод (5) является методом k-го порядка аппроксимации, если
Локальная погрешность многошаговых методов выражается (также, как и для одношаговых) через f и коэффициенты метода. Для этого обозначим для любой дифференцируемой функции
|
через D(t, y, t). Оказывается тогда, что в случае скалярного уравнения
| (7) |
где J О (j(t +tp), (jt)p), а
Действительно, в силу (5) и (6) (jt)p удовлетворяет уравнению
|
откуда, добавив и отняв
| D(tp, j, t) = a0[j(tp) - (jt)p] - tb0(f[tp, j(tp)] - f[tp, (jt)p]) . |
Применив к последнему слагаемому теорему Лагранжа, получим эквивалентное равенству (7) равенство
|
D(tp, j, t) = a0[j(tp) - (jt)p] - tb0 fx(tp, J)[j(tp) - (jt)p] = = [a0 - tb0 fx(tp, J)]e(t, x, t). |
Задача 1.6.5. Выпишите D для явного и неявного двухшаговых методов Адамса.
Задача 1.6.6. Выведите аналог формулы (7) в многомерном случае.
Если отображение f ограничено, то поскольку
| D(t, y, t) = O(tk+1) | (8) |
для всех достаточно гладких функций y. Таким образом, последнее равенство можно рассматривать как эквивалентное определение порядка аппроксимации. Оно удобнее, поскольку в нем вообще не фигурируют решения дифференциального уравнения.
В следующем пункте мы приводим выраженный в терминах коэффициентов as и bs признак выполнения равенства (8).
1.6.9. Теорема о порядке аппроксимации линейных многошаговых методов.
Для того, чтобы линейный p-шаговый метод имел k-й порядок аппроксимации для любой задачи Коши с k раз непрерывно дифференцируемой правой частью необходимо и достаточно выполнения следующих условий
| (9) |
(мы считаем здесь, что 00 = 1).
Д о к а з а т е л ь с т в о. Сохраним обозначение
|
|
в определение D и преобразуем, используя очевидные свойства бесконечно малых
|
|
|
|
|
Теперь эквивалентность соотношений (8) и (9) очевидна.
Например, для явного двухшагового метода Адамса, для которого (см. п. 1.6.5)
Задача 1.6.7. Покажите, что порядок аппроксимации явных p-шаговых методов Адамса
равен p, а
1.6.10. Замечание о постоянном шаге.
Как уже отмечалось, недостатком многошаговых методов является необходимость специального начального запуска метода. Другим недостатком многошаговых методов является сложность процедуры перестройки длины шага, поскольку простые формулы получаются лишь в случае равномерной сетки. Обойти эту трудность можно разными способами. Во-первых, можно строить методы, рассчитанные на неравномерные сетки.
Задача 1.6.8. Постройте явный двухшаговый метод Адамса на неравномерной сетке.
Такие методы требуют пересчета коэффициентов на каждом шаге.
Второй способ заключается в интерполяции по полученным на неравномерной сетке значениям приближенного решения его значений на равномерной сетке (например, с помощью интерполяционных полиномов) и последующем применении многошагового метода с равномерным шагом к новым значениям.
Разумеется, все эти способы увеличивают объем вычислительной,
а также программистской работы, усложняют логику программ
File based on translation from
TEX by TTH,
version 3.05.
Created On 28 May 2002, 18: 26.
Last modified 8 May 2002.