 |
2.1.10. "Спуск" в пространство
F(wh) |  |
Второй способ в некотором смысле обратен к первому. Пусть для каждого h определено некоторое отображение
Lh
из F(W) в F(wh). Расстоянием ||u – uh|| между u и uh назовем число ||Lhu – uh||h.
Это определение также сильно зависит от выбора отображений Lh. Так же, как и в предыдущем случае, эти отображения можно выбирать по-разному. Наиболее распространенный способ заключается в "проектировании" (сужении на сетку wh) F(W) на F(wh): отображения Lh определяются равенствами
т. е. при всех x О wh
См. рис. 1.8, на котором функция u изображена жирной линией, а функция Lhu — светлыми точками.
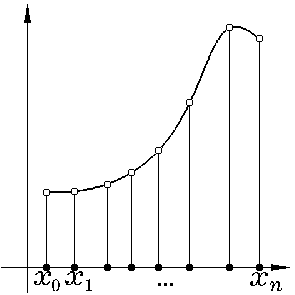
Рис. 1.8.
|
Если пространство F(W) не является пространством непрерывных функций (что не редкость в математическом моделировании механики сплошной среды), то в качестве операторов Lh часто берут "операцию усредненного
значения функции в точке". Например, если W — отрезок [a, b], то Lhu можно определить как (Shu)|wh, где Sh — т. н. усреднение по Стеклову: |
| (Shu)(x) = | 1
2h | т | x+h
x–h | ~
u
| (y) dy; |
|
здесь
~
u
| (y)= | |
м
п
н
п
о | | u(a), если y < a, | | u(y), если a Јy Ј b, | | u(b), если y > b. |
|
|
|
В случае, например, трехмерного W интеграл тx–hx+hu(y)dyзаменяется на
объемный интеграл тттBh(x)u(w) dw по шару Bh(x) радиуса h с центром в x, а 2h — на меру (объем) этого шара. |




