Теоретический анализ гипотетических генных сетей 1

Лихошвай В.А.
Сектор молекулярной эволюции ИЦиГ СО РАН
Матушкин Ю.Г.
Сектор молекулярной эволюции ИЦиГ СО РАН
Фадеев С.И.
Институт математики СО РАН

Генная сеть - группа координированно функционирующих генов, обеспечивающих выполнение определенных жизненно важных функций организмов, регуляцию физиологических процессов, ответ на воздействия внешней среды и т.д. В настоящее время активно развивается математическое моделирование динамики функционирования генных сетей. Здесь выделяются два основных направления. Первое связано с построением и численным исследованим математических моделей реальных генных сетей. Второе направление связано с изучением фундаментальных, системных свойств генных сетей, для чего исследуются теоретические конструкции не обязательно существующие в природе. Реальные генные сети можно разбить на три основных различных класса:

а) поддерживающие в организме устойчивые состояния, характеризующиеся постоянством концентраций веществ (гомеостаз, стационарные состояния);
б) поддерживающие периодические незатухающие изменения концентраций определенных групп веществ (осцилляции);
в) контролирующие необратимые процессы развития (роста), разрушения. Данная классификация реальных генных сетей является эмпирикобиологической и пока не решен вопрос, имеются ли у каждой группы какие-либо принципиальные отличительные особенности на уровне их структурно-функциональной организации. Тем не менее ясно, что в функционировании генных сетей любого типа важнейшую, если не определяющую роль, играют отрицательные и положительные регуляторные связи. Только благодаря наличию отрицательных и положительных связей генные сети приобретают способность к саморегуляции и адекватному реагированию на изменение внешних условий. Поэтому для понимания закономерностей устройства генных сетей, необходимо в первую очередь исследовать роль регуляторных связей в их функционировании.

В настоящей работе мы исследуем закономерности функционирования гипотетических генных сетей (ГГС). ГГС будем строить из двух типов элементарных единиц: генетических элементов и регуляторных связей.

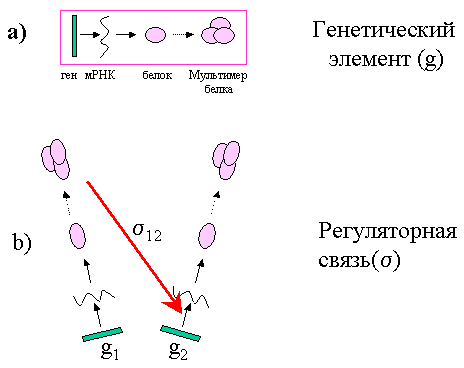
Под генетическим элементом (ГЭ) будет пониматься биологический объект, который содержит ген, мРНК, кодируемую этим геном и белок, кодируемый мРНК. В генетический элемент неявно включаются все процессы, обеспечивающие синтез мРНК, белка, формирование мультимера белка (мономерная форма белка есть частный случай мультимерной) Мультимером кодируемого белка генетический элемент воздействует на другие генетические элементы. (Рис.1a).

Под регуляторной связью будем понимать процесс, посредством которого один генетический элемент (регулятор) действует на другой генетический элемент на любом из уровней экспрессии гена, изменяя (уменьшая или увеличивая) скорость синтеза кодируемого им белка (Рис. 1b).

Рис. 1. Структурные элементы гипотетических генных сетей.
\begin{figure}\begin{center} \epsfxsize=6in %%\epsfysize=254mm \epsfbox{f1.eps} \end{center}\end{figure}

Несколько примеров ГГС приведены на рис.2. На рис. 2а приведена ГГС, состоящая из 2-х генов. В ней продукт гена $g_1$ регулирует синтез (стрелка $\sigma _12)$ продукта гена $g_2$. И наоборот, продукт гена $g_2$ регулирует синтез (стрелка $\sigma _{12})$ продукта гена $g_1$. ГГС на рис 2b,c содержат по три генетических элемента. В первой ГГС каждый генетический элемент регулирует активность следующего элемента. Во второй - каждый генетический элемент регулирует активность двух других элементов. На рис. 2d,e приведены примеры ГГС, содержащих четыре и шесть генетических элементов, соответственно.

Рис. 2. Примеры гипотетических генных сетей.
\begin{figure}\begin{center} \epsfxsize=6in %%\epsfysize=254mm \epsfbox{f2.eps} \end{center}\end{figure}

Отметим очевидное взаимно однозначное соответствие между ГГС и ориентированными графами. Оно устанавливается если представить генетические элементы нумерованными точками, а регуляторные связи - стрелками (Рис. 3). Поэтому каждый ориентированный граф (орграф) порождает определенную ГГС. Например, из четырех генетических элементов можно построить 218 гипотетических генных сетей без автоингибирования (под автоингибированием понимается процесс регулирования активности экспрессии гена собственным белком), из пяти - 9608, из шести - 1 540 944 и т.д. Количество различных ГГС очень быстро растет с ростом числа генетических элементов.

Рис. 3. Примеры структурных графов гипотетических генных сетей.
\begin{figure}\begin{center} \epsfxsize=6in %%\epsfysize=254mm \epsfbox{f3.eps} \end{center}\end{figure}

Динамику функционирования ГГС опишем следующей системой дифференциальных уравнений.


\begin{displaymath} {\textstyle{{dp_{i}} \over {dt}}} = {\textstyle{{(\alpha _{i... ...{i,j} } )}}} }} - \beta _{i} p_{i} ,\,\,i = \overline {1,n.} \end{displaymath} (1)

Здесь, n обозначает количество генетических элементов $g_i$; $p_i$ - концентрацию белка, кодируемого $g_i$; $D_{i} = {\left\{ {j_{1} ,...,j_{k_{i}} {\left\vert {k_{i,j_{l}} h_{i,j_{l}} + \gamma _{i,j_{l}} m_{i,j_{l}} \ne 0,\,\,l = 1,..,k_{i}} \right.}} \right\}}$ - множество номеров генетических элементов, являющихся регуляторами $g_i$; $\beta _i$ - константы скоростей процессов, уменьшающих концентрацию $p_i$ (деградация, транспорт из компартмента и т.д.); $\alpha $$_{i}$, $\gamma $$_{i,j}$, $\kappa $$_{i,j}-$ коэффициенты, регулирующие активность синтеза белка $p_{{ i}}$ регуляторами $p_{{ j}}$; $h_{i,j}$, $m_{i,j} -$ степень влияния $p_{j}$ на активность $g_{{ i}}$. В простейшем случае $h_{i,j}$, $m_{i,j}$ имеют смысл размерности (в смысле количества субъединиц) молекулы регулятора, в общем же случае характеризуют сложность процесса регуляции и могут быть не целыми числами. Из биологических соображений все $\beta $$_{i}$, $\alpha $$_{i}$, $\gamma $$_{i,j}$, $\kappa $$_{i,j},$ $h_{i,j}$, $m_{i,j}$ являются неотрицательными числами. Если $\kappa $ $_{i,j}h_{i,j}=0,$ то j-й генетический элемент является ингибитором i-го, если $h_{i,j}$$ \ge $m$_{i,j{ ,}} $ то связь является позитивной, при 0<$h_{i,{ j}}$<m$_{{ i},j}$ регуляторная связь является смешанной - при малых $p_j$ активность i-го генетического элемента с ростом значения $p_j$ будет возрастать, а при больших $p_j$ - убывать.

Заметим, что формально допустимое выполнение строгого неравенства $h_{i,j}>m_{i,{j}}$ означает неограниченную активацию, что с биологической точки зрения является бессмысленным, поэтому естественно принять дополнительные условия $h_{i,j}$$ \le $m$_{i,{ j}}$ и $\kappa $$_{i,j}=0$, если $\gamma $$_{i,j}=0$. Назовем системы (1) ГГС-моделями. Очевидно, что $\Delta =\{D_i\}_{{ i}{ = }{ 1},...,{ n}}$ полностью определяют структуру гипотетической генной сети, структуру ГГС-моделей и орграф, соответствующий ГГС. Совокупность $\Delta $ назовем структурой генной сети, описываемой системой (1), а орграф будем называть структурным графом.

Исследование свойств систем вида (1) позволят нам адекватно судить о свойствах соответствующих ГГС. Особенно интересны предельные свойства этих систем. Численные расчеты показывают, что ГГС-модели могут иметь как точки покоя, так и предельные циклы. Далее мы ограничимся рассмотрением ГГС-моделей при $\kappa _{{ i},{ j}}$=0, h $_{{ i}{ ,}{ j}}$=0, $\alpha _{{ i}}=\alpha $, $\beta _{{ i}}$=1, $\gamma _{{ i},{ j}}$=1, m$_{{ i}}$=m. С биологической точки зрения это означает, что мы будем рассматривать только отрицательные регуляторные связи и будем считать, что все гены являются идентичными, с точки зрения кинетики процессов. В результате принятия данного ограничения в системах (1) остается только 2 независимых параметра $\alpha $ и $\beta $. Тогда, ГГС-модель генной сети Рис. 3a имеет вид

\begin{displaymath}dp_{{ 1}}/dt=\alpha /(1+p_{{ 2}}^{{ m}})-p_{{ 1}},\end{displaymath}


\begin{displaymath}dp_{{ 2}}/dt=\alpha /(1+p_{{ 1}}^{{ m}})-p_{{ 2}}.\end{displaymath}

При {m<2, $\alpha $>0} и при {m$ \ge $2, 2$ \ge \alpha $>0} у нее имеется только одно устойчивое состояние, а при $\{m \ge 2$, $\alpha $>2} уже имеется два устойчивых состояния. ГГС-модель генной сети Рис. 3b имеет вид

\begin{displaymath}dp_{{ 1}}/dt=\alpha /(1+p_{{ 3}}^{{ m}})-p_{{ 1}},\end{displaymath}


\begin{displaymath}dp_2/dt=\alpha /(1+p_1^m)-p_2,\end{displaymath}


\begin{displaymath}dp_3/dt=\alpha /(1+p_2^m)-p_3\end{displaymath}

и при $\{m<2, \alpha >0\}$ или $\{m \ge 2, 1 \ge \alpha >0\}$ у нее имеется только одно устойчивое состояние, при $\{m \ge 2, 2>\alpha >1\}$ имеется один устойчивый предельный цикл и одна устойчивая точка, а при $\{m \ge 2, \alpha \ge 2\}$ имеется один устойчивый предельный цикл.

Предельное поведение ГГС-моделей усложняется по мере увеличения числа генетических элементов и регуляторных связей. Например, если рассмотреть ГГС, состоящую из шести генов (Рис. 4с), в которой каждый ген ингибирует пять остальных, то поведение соответствующей ГГС-модели уже достаточно сложно. Не вдаваясь в подробности, отметим, что при $\{m \ge 6, \alpha \ge 6\}$ у данной системы найдено 83 точки покоя, из которых только 6 являются устойчивыми.

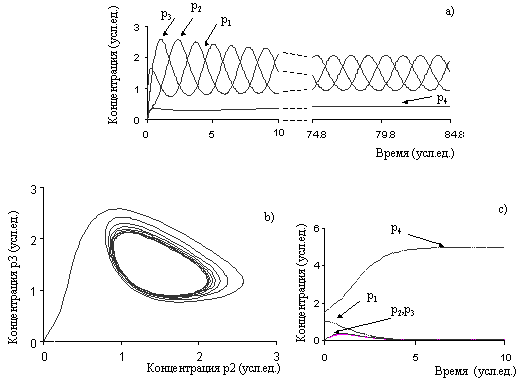
В качестве графической иллюстрации приведем пример численного расчета ГГС-модели генной сети (Рис. 4а). Расчеты проводились при m=3 и $\alpha =5$. В простейшей интерпретации значение m=3 означает, что активными формами ингибиторов являются тримеры белков. Данная генная сеть при выбранных значениях m и $\alpha $ имеет два предельных режима функционирования. При задании начальных концентраций $р_1=1$, $р_2=р_3=р_4=0$ реализуется осциллирующий режим, при котором концентрации всех продуктов испытывают незатухающие периодические колебания (Рис. 5a). На рис. 5b тот же расчет приводится в фазовых координатах (р2, р3). При задании начальных данных $р_1=1$, $р_2=р_3=0$, $р_4=1.5$ эта же система выходит в область стационарного режима, который характеризуется постоянными во времени значениями концентраций всех четырех компонентов модели (Рис. 4c).

Рис. 4. Расчет динамики функционирования генной сети Рис. 2d при различных начальных условиях: a,b) р1=1, р2=р3=р4=0; c) р1=1, р2=р3=0, р4=1.5.
\begin{figure}\begin{center} \epsfxsize=6in %%\epsfysize=254mm \epsfbox{f4.eps} \end{center}\end{figure}

Рассмотренные примеры показывают, что имеется широкое разнообразие предельных режимов функционирования ГГС. С биологической точки зрения особенно важным является выявление таких закономерностей, которые непосредственно определяются их структурой. С математической точки зрения проблема сводится к описанию фазовых портретов ГГС-моделей. Ниже мы формулируем эмпирические критерии и гипотезы, которые позволяют выявлять наличие устойчивых режимов функционирования гипотетических генных сетей, включая точки покоя и предельные циклы и подсчитывать их количество.

Для симметричной генной сети число устойчивых точек и предельных циклов однозначно определяется по графу структуры отрицательных связей всего лишь двумя параметрами.

Сначала рассмотрим более узкий класс генных сетей. Пусть, по-прежнему, n обозначает количество генетических элементов (ГЭ) в сети. Зафиксируем натуральное число $k\in \{2,\ldots , n\}$. ГЭ сети расположим по кольцу и будем считать, что каждый ГЭ является ингибитором следующих (по часовой стрелке) (k-1) ГЭ (Рис. 4b,c). В этом случае n и k полностью определяют структуру таких сетей. Обозначим модели этих сетей как M(n,k), а сами генные сети, в силу кольцевой симметрии обозначим через S(n,k). При фиксированном n существует ровно n-1 различных симметричных ГГС (для каждого k=2,...,n), в которых ГЭ не является ингибитором собственной активности, но является ингибитором хотя бы одного гена. В таблице приведены результаты численного анализа устойчивых режимов функционирования всех возможных вариантов симметричных сетей, с числом генов от 2 до 9. В ходе анализа осуществлялось численное решение системы дифференциальных уравнений (1) при различных начальных значениях концентраций $P_i$ (i=1,...,n). Расчеты проводились при m=k+1, $\alpha =k+1$. Для моделей, приведенных в строках 1-9 таблицы, были обнаружены только устойчивые точки, а для моделей, приведенных в строках 10-12 таблицы, напротив, устойчивых точек не обнаружено, а найдены устойчивые предельные циклы, в количестве 1, 2 и 3, соответственно.

Итак, предельные свойства симметричных ГГС с различными структурными графами различаются. В результате анализа данных таблицы и других симметричных сетей мы сформулировали следующий критерий, который устанавливает связь структуры симметричных сетей с предельными режимами их функционирования при достаточно больших значениях m и $\alpha $.

(n,k)-Критерий. Если n делится нацело на k, то существуют такие m$_{{ 0}}$ и $\alpha $$_{{ 0}}$, что при любых m$ \ge $m$_{{ 0}}$ и $\alpha \ge \alpha $$_{{ 0}}$ модель M(n,k) имеет k устойчивых состояний. Устойчивых незатухающих периодических режимов у данной системы нет. Если n не делится на k нацело, то существуют такие m$_{{ 0}}$ и a$_{{ 0}}$, что при любых m$ \ge $m$_{{ 0}}$ и a$ \ge $a$_{{ 0}}$ у M(n,k)-модели существует d (d - наибольший общий делитель n и k) устойчивых периодических режимов и в этой области у нее нет других режимов функционирования.

Мы предполагаем, что поведение симметричных генных сетей построенных из идентичных ГЭ, при условии что ингибиторы активности ГЭ являются мультимерами достаточно высокого порядка (m$ \ge $m$_{{ 0}}$), а скорости синтеза белков при отсутствии ингибирования достаточно высоки ( $\alpha \ge \alpha _{{ 0}})$, полностью характеризуется структурой генной сети и это поведение описывается (n,k)-критерием.


Табл. Список M(n,k)-моделей, изученных численно, и количество найденных у них устойчивых
особых точек и предельных циклов.

№ Наименование модели$^{{ a}{ )}}$ P$^{}$ C$^{}$
1 M(2,2),M(4,2), M(6,2), M(8,2) 2 0
2 M(3,3), M(6,3), M(9,3) 3 0
3 M(4,4),M(8,4) 4 0
4 M(5,5) 5 0
5 M(6,6) 6 0
6 M(7,7) 7 0
7 M(8,8) 8  
8 M(9,9) 9  
9 M(3,2), M(4,3), M(5,2), M(5,3), M(5,4), M(6,5), M(7,2), M(7,3), M(7,4), M(7,5), M(7,6), M(8,3), M(8,5), M(8,7), M(9,2), M(9,4), M(9,5), M(9,7) 0 1
10 M(6,4) 0 2
11 М(9,6) 0 3

a) пояснения см. в тексте, P- количество устойчивых точек,$^{}$C - количество устойчивых циклов (численные расчеты проводились при m=k+1, $\alpha $=k+1).

Режимы функционирования генных сетей произвольной структуры.

Расчеты показывают, что предельные свойств ГГС произвольной структуры тесно связаны с свойствами конечных автоматов, которые определяются следующим образом.

Пусть орграф задан. По-прежнему, пусть $\Delta $={D$_{{ i}}$} $_{{ i}{ =} { 1},...,{ n}}$ структура графа. Далее будем рассматривать только связные графы. Зафиксируем некоторое натуральное p и зададим некоторый целочисленный вектор (x$_{{ 1}}$,...,x$_{{ n}})$, где $1\le x_{{ i}} \le p$. Припишем вершине i графа число $x_{{ i}}$, которое назовем весом. Введем n p-значных рекурсивных функций


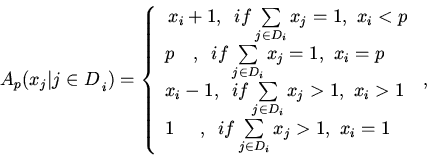
\begin{displaymath} A_{p} (x_{j} {\left\vert {j \in D} \right.}_{i} ) = {\left\{... ...x_{j}}} > 1,\,\,x_{i} = 1} \hfill \\ \end{array}}} \right.}, \end{displaymath}

аргументы и значения которой являются натуральными числами 1, ..., р.

Применив итерационную процедуру: $х^+_1 = A_ p(x_j\vert j \in D_ 1, ..., х^+_ n=A_p(x_j\vert j\in D_ n)$, вычислим новый весовой вектор (x $^{{ +}} _{{ 1}}$,...,x $^{{ +}} _{{ n}})$. Очевидно, что вычисление весового вектора (x $^{{ +}} _{{ 1}}$,...,x $^{{ +}} _{{ n}})$ по весовому вектору (x$_{{ 1}}$,...,x$_{{ n}})$ представляет целочисленную векторную функцию, которая отображает целые точки куба [1, p]$^{{ n}}$ в себя. Обозначим данную функцию через А $_{{ n}{ \vert} { \Delta} ,{ p}}$ и назовем р-значным автоматом генной сети. Последовательное применение автомата А $_{{ n}{ \vert} { \Delta} ,{ p}}$ к вектору (x$_{{ 1}}$,...,x$_{{ n}})$ порождает весовую траекторию

А $^{{ 0}}_{{ n}{ \vert} { \Delta} ,{ p}}$(x$_{{ 1}}$,...,x $_{{ n}}) \quad \equiv $ (x$_{{ 1}}$,...,x$_{{ n}})$, (x $^{{ +}} _{{ 1}}$,...,x $^{{ +}} _{{ n}}) \quad \equiv $ А $_{{ n}{ \vert} { \Delta} ,{ p}}$(x$_{{ 1}}$,...,x$_{{ n}})$,

А $^{{ 2}}_{{ n}{ \vert} { \Delta} ,{ p}}$(x$_{{ 1}}$,...,x $_{{ n}}) \quad \equiv $ А $_{{ n}{ \vert} { \Delta} { ,}{ p}}$(А $_{{ n}{ \vert} { \Delta} ,{ p}}$(x$_{{ 1}}$,...,x$_{{ n}}))$, А $^{{ 3}}_{{ n}{ \vert} { \Delta },{ p}}$(x$_{{ 1}}$,...,x $_{{ n}}) \equiv $А $_{{ n}{ \vert} { \Delta} ,{ p}}$(А $^{{ 2}}_{{ n}{ \vert} { \Delta} ,{ p}}$(x$_{{ 1}}$,...,x$_{{ n}}))$, ..., А $^{{ m}}_{{ n}{ \vert} { \Delta} ,{ p}}$(x$_{{ 1}}$,...,x $_{{ n}}) \equiv $А $_{{ n}{ \vert} { \Delta} { ,}{ p}}$(А $^{{ m}{ -} { 1}}_{{ n}{ \vert} { \Delta },{ p}}$(x$_{{ 1}}$,...,x$_{{ n}}))$, ...

Очевидно, каждая точка целочисленного куба [1, p]$^{{ n}}$ может быть принята в качестве весового вектора и она порождает собственную весовую траекторию. В силу того, что в кубе [1, p]$^{{ n}}$ имеется $p^{{ n}}$ целочисленных точек, то всего имеется $p^{{ n}}$ весовых траекторий и в каждой траектории через конечное число итераций возникнут циклические повторы. Выделим у каждой траектории цикл минимальной длины. Будем считать две траектории эквивалентными, если они содержат идентичные циклы. Нетрудно убедиться, что это отношение удовлетворяет всем аксиомам эквивалентности. Поэтому оно разбивает все целочисленные точки куба [1, p]$^{{ n}}$ на непересекающиеся классы эквивалентности. Назовем длину минимального цикла любого представителя класса эквивалентности длиной этого класса.

Рассмотрим теперь некоторый класс эквивалентности и возмем из него некоторую траекторию. Назовем класс вырожденными, если в цикле траектории имеются вершины, принимающие попеременно веса 0 и 1. Обозначим через C $_{{ n}{ \vert} { \Delta} ,{ p}}$ множество классов эквивалентности, порожденное функцией А $_{{ n}{ \vert} { \Delta} ,{ p}}$.

Сравнительный анализ траекторий порождаемых ГГС-моделями и р-значными автоматами позволил нам выявить следующие закономерности, которые мы оформили в виде двух гипотез.

Гипотеза 1 (об устойчивых точках). Для всех р>0 C $_{{ n}{ \vert} { \Delta} ,{ p}}$ содержат равные количества классов длины 1. Существуют такие m$_{{ 0}}$ и $\alpha _{{ 0}}$, что при любых m$ \ge $m$_{{ 0}}$ и $\alpha \quad \ge \quad \alpha _{{ 0}}$ количество устойчивых точек гипотетической генной сети, имеющей структуру $\Delta $, в точности равно количеству классов длины 1.

Гипотеза 2 (о предельных циклах). Существуют такие m$_{{ 0}}$ и $\alpha $$_{{ 0}}$, что при любых m $ \ge $ m$_{{ 0}}$ и $\alpha \quad \ge \quad \alpha $$_{{ 0}}$ суммарное количество циклов соответствующей генной сети, включая устойчивые и неустойчивые, не превосходит минимального числа невырожденных классов длины больше 2, где минимум берется по всем р$ \ge $2. Для симметричных генных сетей при некотором р достигается точное равенство.

Данные гипотезы носят эмпирический характер и пока не доказаны в общем виде. Однако, даже не имея соответствующих доказательств, приведенные (n,k)-критерий и гипотезы, дополненные численными методами, позволяют уже сейчас представить некоторые детали функционирования генных сетей. Например из гипотезы 2 следует, что для симметричных генных сетей для некоторого р, возможно достаточно большого, общее количество предельных циклов, как устойчивых, так и неустойчивых, равно количеству невырожденных классов, порожденным р-значным автоматом данной сети. Так как численными методами интегрирования устойчивые циклы симметричных генных сетей выявляются достаточно легко, то ненулевая разница будет свидетельствовать о наличии у нее неустойчивых предельных циклов. Например, генная сеть S(6,2) согласно (n,k)-критерию при достаточно больших значениях $m \ge m_ 0$ и $\alpha \ge \alpha _{{ 0}}$ имеет только две устойчивые точки и не имеет устойчивых предельных циклов. Исследование свойств р-значных автоматов данной сети выявляет у них при $р \ge 128$ наличие одного невырожденного класса. Следовательно для симметричной генной сети прогнозируется существование неустойчивого предельного цикла. И действительно, исследование модели М(6,2) аналитическими методами, а также с помощью пакета ``STEP'', выявляет при $m_0 \ge 2$ и $\alpha _{{ 0}} \ge 2$ две устойчивые и три неустойчивые точки покоя и один неустойчивый предельный цикл. Следует отметить, что поиск неустойчивого предельного цикла в сети S(6,2) был предпринят и его удалось обнаружить только благодаря тому, что из гипотезы 2 и $(n,k)$-критерия следует его существование.

Итак, в настоящей работе мы предлагаем математический аппарат для описания гипотетических генных сетей и формулируем ряд гипотез о закономерностях их функционирования, требующих дальнейшего теоретического обоснования. Представленный подход открывает возможность для анализа структуры реальных генных сетей. Мы полагаем, что дальнейшее развитие данного подхода позволит подойти к решению практически важной задачи конструирования генных сетей с наперед заданными динамическими свойствами и предельными режимами функционирования. Тот факт, что качественное поведение генной сети зависит от структуры графа и способно кардинально меняться при появлении хотя бы одной новой или исчезновении ранее существовавшей регуляторной связи, дает новые возможности для объяснения закономерностей эволюции генных сетей (в частности их эволюционного усложнения), а также интерпретации влияния мутаций на функцию генетических сетей и контролируемых ими процессов.

1
Работа получила частичную финансовую поддержку ГНТПР "Геном человека" (106), Грантов РФФИ 01-07-90376, 00-04-49229, 00-04-49255, 00-07-90337, 99-07-90203, 98-04-49479, 98-07-90126, 98-07-91078 и Междисциплинарного интеграционного проекта N65 СО РАН "Моделирование фундаментальных генетических процессов и систем".
Ваши комментарии
[SBRAS]
[Головная страница]
[Конференции]
[СО РАН]

© 2001, Сибирское отделение Российской академии наук, Новосибирск
© 2001, Объединенный институт информатики СО РАН, Новосибирск
© 2001, Институт вычислительных технологий СО РАН, Новосибирск
© 2001, Институт систем информатики СО РАН, Новосибирск
© 2001, Институт математики СО РАН, Новосибирск
© 2001, Институт цитологии и генетики СО РАН, Новосибирск
© 2001, Институт вычислительной математики и математической геофизики СО РАН, Новосибирск
© 2001, Новосибирский государственный университет
Дата последней модификации Tuesday, 11-Sep-2001 20:11:17 NOVST