Information model on categories "voice/unvoice'' of segments in speech

Skljarov O.P.
Research Institute of Ear, Throat, Nose and Speech, St.-Petersburg

Annotation:

In the offered paper the dynamic regimes peculiar to the rhythmic structure of normal speech and stuttering are detected. Within the framework of the offered mathematical model the factors resulting to change of these regimes are established. It allows to realise in practice optimum strategy of a correction of the rhythm for each stutter individually.

Introduction.

In the last decade the significant amount of tasks in physics and engineering were successfully resolved by methods of critical phenomenon theory. Rather often the dynamics of these systems near critical point was described by means of new topic of mathematics - so named dynamical chaos.

But it's yet rather surprisingly that this especially engineering approach has appeared even more productive for explanation of many effects in such far from an engineering area as stuttering [2, 3] In this paper we show the large-scale temporal structure of normal and destroyed speech possesses the dynamical regimes set. As it has appeared the change of these regimes was controlled by different external both instrumental and so-called learning influences on dynamical system. In our case this system is speech production mechanism of some person, and these influences may be, for example, acoustic feedback, or, for example, the set of different governing, or so-called "learning'' procedures applied to this person. In particular these external influences are used to drive such temporal characteristics of stutters as speech temp and speech rhythm in area of its normal values.

In this paper we described our method of registration of large-scale temporal structure of speech signals. This method based on segmentation of speech acoustical signal in accordance with the principle of "Voice/Unvoice''. Normalized durations of voiced and unvoiced segments were organized as the point set. Then on the base of model-less approach we estimate such characteristics of critical behavior for system as Hausdorff dimensionalities of experimentally measured point set and its information Kolmogorov entropy. On the base of these characteristics we conclude that system has as regular fractal properties and irregular chaotic properties. Thus the system in topic has critical point in scenario of its route to chaos in relation of control or "learning'' parameter. The features of this scenario and correlation existing between experimental data and model offered us have allowed us to accept the model of point logistic mapping between the normalized segment duration.

Then we study the possibilities of this model to be controlled by external influences. We regard the case of external general feedback (logo-therapeutic actions) which allowed change one dynamical regime, for example, stuttering, on another regime, for example, normal speech.

These model's possibilities were supported by experiments "in vivo'' carried out by us with our colleague, when temporal characteristics of destroyed speech were reduced in a norm by methods of correction actions.

Segmentation

Speech signals were imputed in computer. These signals were normalized on all dynamic range of computer. After preliminary particular smoothing of signals we determined threshold of segmentation for each individual subject with the help of handling of test phrase. The amplitude threshold grows gradually from zero with a rather small step so long as for the first time six (and only six) Voice segments are occurred in this test phrase "papa, papa, papa''. For determination of the moment when Unvoice segment begins we used some parameter of temporal resolution (approximately 40 msec). If the following sample did not occur at t>40 msec, we considered that the Voiced segment was completed and Unvoice segment began. Process of determination threshold is broken if coefficient of segment durations' variation did not exceed 0.5. Then this threshold was used for automatic segmentation of the basic signal. The comparison of results, obtained with help of our automatic segmentation and results of hand-operated segmentation has given satisfactory coincidence. For each speech sample the normalized duration of Voice and Unvoice segments were calculated. These durations are organized as a point set on unit interval [0, 1]. The mean duration on this set we named V/U-temp (rate) and variation coefficient on the same set is named as a degree of violation of V/U-rhythm or simply - V/U-rhythm (Skljarov, 1999). In case of point set consisting only of Voce segments these variables are named V-temp and V-rhythm.

The fractal-chaotic nature of speech.
Hausdorff dimensionalities.

Reconstruction complex system dynamics is possible by means of the model-less method with help of temporal experimental sequence of only one but essential variable. In our case this sequence is train of segment's duration. Information contained in this sequence allows to identify some essential peculiarities of dynamical system generating this sequence or, in another words, V/U-rhythm, or else point set on interval [0, 1].

In particular, this rhythm allows reconstruct the Hausdorff dimensionality of studied point set. In continuous case this dimensionality corresponds to dimensionality of attractor to which is tightened the phase trajectory of dynamics task.

For determination of Hausdorff dimensionality of some point set which occupies domain with volume $L^{D}$ in -dimension space let's cover this set by boxes with volume $l^{D}$ . The minimal number of these boxes for covering our point set is $M(l) = L^{D}(1 / l)^{D}$ . From this expression we can get the follow approximate estimation for :

$\begin{displaymath} D = {\mathop {\lim} \limits_{l \to 0}} {\left[ {{\frac{{\ln M(l)}}{{\ln (1 / l)}}}} \right]}. \end{displaymath}$

(1)

In practice more convenient estimation of is take out from special mathematician construction named as Renyi dimensionality $D_{f}$ , related with value of probability of point's being in -th cell raised to the -th power [1]

$\begin{displaymath} D_{f} = {\mathop {{\mathop {\lim} \limits_{l \to 0}} \left( ... ...M(l)} {p_{i}^{f}}} } \right)}}{{\ln l}}}; \quad f = 0,1,2,... \end{displaymath}$

(2)

At $f \to 0$ we have from formulae (2):

$\begin{displaymath} D_{0} = - {\mathop {\lim} \limits_{l \to 0}} \left( {\ln {\s... ...mits_{l \to 0}} {\frac{{\ln M(l)}}{{\ln l}}}}\limits_{}} = D, \end{displaymath}$

(3)

i.e. Renyi dimensionality $D_{0}$ at $f \to 0$ coincides with Hausdorff dimensionality introduced by formulae (1). By virtue of the monotone $D_{f}$ as function Renyi dimensionality decreases as function of power and follow relation is fulfilled: $D_{2} \le D_{0} = D$ . Thus the greatest lower bound of Hausdorff dimensionality is $D_{2}$ represented as:

$\begin{displaymath} D_{2} = {\mathop {\lim} \limits_{l \to 0}} {\frac{{\ln \left... ...i = 1}^{M(l)} {p_{i}^{2}}} } \right)}}{{\ln l}}} \quad {\rm .} \end{displaymath}$

(4)

Taking into account that probability $p_{i}$ of point's being in th cell is $p_{i} = {\mathop {\lim} \limits_{N \to \infty}} N_{i} / N$ , where is summary number of points, or number of segments-elements of rhythm, and $N_{i}$ is number of elements being in -th cell, formulae (4) may be calculated from experimental measured segments. 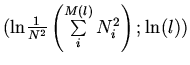In practice the greatest lower bound of attractor dimensionality $D_{2}$ is calculated as tangent of slope angle of the linear regression of following points $({\rm l}{\rm n}{\frac{{{\rm 1}}}{{N^{2}}}}\left( {{\sum\limits_{i}^{M(l)} {N_{i}^{2}}} } \right);{\rm l}{\rm n}(l))$ , calculated at different .

Thus Hausdorff or fractal dimensionalities for normal speech and for stuttering are: Normal speech: $D_{2}$ =1,05 $\pm \quad \sigma _{\Sigma}$ =1,05 $\pm$ 0,14; Stuttering: $D_{2}$ =0,56 $\pm \quad \sigma _{\Sigma}$ =0,56 $\pm$ 0,12. The fractal dimensionality for stuttering rhythm $D_{2}$ =0,56 is evidence of fractal nature of this rhythm. As we shall show in next topic of paper, Hausdorff dimensionality $D_{2}$ =1,05 for normal speech rhythm corresponds to chaotic nature of this rhythm. This correspondence would be revealed by model-less estimation also, with help of Kolmogorov entropy technique.

Kolmogorov entropy or Laypunov index.

Let's generalise the definition of the information entropy $I_{0}$ (Shennon entropy). By definition Shennon entropy is this information which we obtain when we are knowing about point $x_{0}$ , that it is being in any concrete of subintervals, on which the unit interval [0, 1] is divided. For this information we have follow formulae:

$\begin{displaymath} I_{0} = - {\sum\limits_{i = 1}^{n} {{\frac{{1}}{{n}}}\log _{2} {\frac{{1}}{{n}}} = \log _{2} n}} , \end{displaymath}$

(5)

Let's generalise this formulae on a regarding case of V-rhythm of speech. It appears, in case of a speech V-rhythm this generalisation supposes a possibility of an experimental evaluation of an information entropy. Let's regard rhythm ${\rm {\bf T}} = (T_{1} ,...,T_{N} )$ (V-elements of rhythm is ordered by members of natural series). This rhythm is located on interval [0, 1] covered by cells with sufficiently small size . Let's spy on state of system as our rhythm is developed. Let $P_{i_{1} ,...,i_{n}}$ is jointly probability of following event: element $T_{1}$ is in a cell with number $i_{1}$ , $T_{2}$ is in a cell with number $i_{2}$ and so on. By analogue with formulae (5) knowing that rhythm is in concrete division $i_{1}^{\ast} ,...,i_{n}^{\ast}$ with cells of its sizes , we receive information (at the condition of knowing of a priori probabilities $P_{i_{1} ,...,i_{n}} )$ :

$\begin{displaymath} I_{n} = - {\sum\limits_{i_{1} ,...,i_{n}} {P_{i_{1} ,...,i_{n}} \ln P_{i_{1} ,...,i_{n}}} } \end{displaymath}$

(6)

Let's definite the magnitude of information dissipated by the system on the 1-th step of rhythm generation as $I_{n} - I_{n + 1}$ . Then Kolmogorov entropy or K-entropy for rhythm should be determined as the mean value of information generated by system in one iteration:

$\begin{displaymath} K = {\mathop {\lim} \limits_{l \to 0}} {\mathop {\lim} \limi... ......,i_{n}} {P_{i_{1} ,...,i_{n}} \ln P_{i_{1} ,...,i_{n}}} } \end{displaymath}$

(7)

With the purpose of the estimation of K-entropy with help of experimental data let's introduce generalised construction so-called Renyi entropy:

$\begin{displaymath} K_{f} = - {\mathop {\lim} \limits_{l \to 0}} {\mathop {\lim}... ... {\sum\limits_{i_{1} ,...,i_{n}} {P_{i_{1} ,...,i_{n}} ^{f}}} \end{displaymath}$

(8)

It is possible to show that the following relations are fair: $K_{1} = K$ and $K_{{f}'} \le K_{f}$ for $f \le {f}'$ .

The greatest lower bound of the K-entropy is selected as $K_{2}$ especially, and this bound is frequently rather simply for evaluations (in any case, in case of one-dimension of speech V-rhythm), and follow the equality is observed:

$K_{2} = - {\mathop {\lim} \limits_{l \to 0}} {\mathop {\lim} \limits_{n \to \i... ...\to 0} }{\mathop {\lim} \limits_{n \to \infty}} {\frac{{1}}{{n}}}\ln C_{n} (l)$ as correlation integral $C_{n} (l)$ in case of speech V-rhythm we use the following formulae:

$\begin{displaymath} C_{n} (l) = {\mathop {\lim} \limits_{N \to \infty} }{\frac{... ...ert {\rm {\bf T}}_{i}^{(n)} - {\rm {\bf T}}_{j}^{(n)} \vert ). \end{displaymath}$

(9)

The formulae (9) is generalisation of the definition of correlation integral for scalar case [1]. For clearing of term "correlation'' in definition of correlation integral lets regard oscillation system with attractor kind of limit cycle with dimensionality 1. Any pair of points on the limit cycle will be evidently demonstrated the strong correlation. On the another side if this pair of points belongs to process with chaotic dynamics than with accordance with definition of such process interval between these points should be increased with time exponentially because of positive Lypunov index. Surely, correlation of pairs of points should be more less than in case of periodic moving.

In case of general correlation integral $C_{n} (l)$ its deviation from zero will serve as measure of influence of a vector of the elements of rhythm ${\rm {\bf T}}_{i}^{(n)} = (T_{i} ,T_{i + 1} ,...,T_{i + n} )$ on remaining vectors ${\rm {\bf T}}_{j}^{(n)} = (T_{j} ,T_{j + 1} ,...,T_{j + n} )$ ( $i \ne j)$ , instead of influence of single element on the remaining elements, as it was provided by the definition (9).

As the physical sense of a generalized correlation integral $C_{n} (l)$ is admissible to treat (in the correspondence with the formulae for correlation dimensionality $R = {\mathop {\lim} \limits_{l \to 0}} {\left[ {{\frac{{\ln [C(l)]}}{{\ln l}}}} \right]}$ , obtained by analogy to the formula for Hausdorff dimensionality) as generalisation of the relation $C(l) \sim (l)^{R}$ on -dimensionality case: $C_{n} (l) \sim (l)^{nR}$ , there is admissible realisation of the following equality:

$\begin{displaymath} C_{n + 1} (l) = C_{n}^{{\frac{{n + 1}}{{n}}}} (l) \end{displaymath}$

(10)

Using taken the logarithm, the equality (11) can be rewrite in the following view:

$\begin{displaymath} K_{2} = - {\mathop {\lim} \limits_{l \to 0}} {\mathop {\lim}... ...\ln {\left[ {{\frac{{C_{n} (l)}}{{C_{n + 1} (l)}}}} \right]}. \end{displaymath}$

(11)

In case of the speech rhythm this expression supposes a construction of rather simple algorithm for computer evaluation of the lower boundary of the K-entropy $K_{2}$ from experimental data.

It would possible see [2,3], that with $n \to \infty$ and $l \to 0$ K-entropy for normal speech is positive and is restricted, that corresponds to the determination chaos in rhythm of fluency speech; otherwise the lower boundary of an entropy is negative for fluency disorders in speech. It allows zero value of the K-entropy, and thus, the availability of the periodic forms is possible. These periodic forms are driving with zero information entropy. As the K-entropy represents the information generated by a system, the above mentioned evidence allows us to characterise chaos as this state of system dynamics in which it "generates", or "dissipates" some information. Thus analysis of phenomenological segmental speech structure shows that this structure has chaotic nature for normal speech and fractal structure for stuttering. This conclusion forces us to search for such mathematical model of rhythm generation process which at first, would have both chaotic and fractal dynamic regimes, and secondly, this model should be compatible with representations about neural control by process of speech.

Model of the speech V/U- rhythm.

At first, to satisfy with the first condition let's remember that Hausdorff dimensionality is $D_{2}$ =0,56 for stuttering rhythm and is $D_{2}$ =1,05 for normal speech rhythm. We can see a rather well coincidence of our results with theoretical estimations of Hausdorff dimensionalities for logistics mapping $y_{n + 1} = ry_{n} (1 - y_{n} )$ found in [1], ( $y_{n} \in [0,1])$ : $D \approx 1$ with the controlling parameter appropriate to zone of chaos ( $r \approx 4)$ and $D \approx 0.5$ - with the controlling parameter appropriate to the boundary between bifurcation zone and zone of chaos ( $r \approx r_{\infty} )$ . Just such regions of the best correlation of the theoretical and experimental rhythm in depth of chaos zone we observed for normal speech whereas the profile of such correlation for stuttering has brightly expressed splash in boundary zone (Skljarov, 1999, 2000). Just on the approach from the left to the boundary of chaos and bifurcation zone the logistics mapping, has the attractor with fractal dimensionality 0.54 on the super cycle of the infinite cascade of period doubling.

Secondly, the other condition concerning the compatibility with neuronal control mechanism is satisfied by result of computational experiment with artificial neuronal Hopfield net [5]. In this paper there was shown, that the Hopfield nets have exactly same route to chaos as function of control parameter or parameter of "learning" $\eta$ , as logistics map has with a control parameter $r = \eta$ . In paper [2] we have found conditions of isomorphism of this route to chaos diagram and diagram for possible segment's duration in system of rhythm generation. These conditions concern specificity of the neuronal acoustical mechanism of reception of rhythmically organised speech and so they wouldn't described in this context. Besides in paper [3] was demonstrated exterior action on the Hopfield net (or the feedback) must result to the displacement of the scenario of route relatively itself, that is, in other words, to change of the dynamic regime. The isomorphism, found by us, and results on simulation of influence of the generalized feedback has allowed us to plan paths of a intelligent modification of the dynamic regime of the system or, in other words, to control speech rhythm. In the result it has allowed to correct fluency of speech with the help of inclusions of the computer model of control as the link of the feedback in the line-up "logo therapeutic expert-stutter".

Intelligent control of speech.

Above the possibility of control of rhythm regime was established in principle. In practice the influence on a dynamics regime is rendered by the logo therapeutic expert by means of intelligent use of various receptions for statement of breath, voice function, articulations. However these receptions should be used for each stutter individually with the purpose of optimum carrying out of temporal the features of speech to normal values. Entered above V-temp and V-rhythm can serve as such features, as there was shown by us in [2,3,4] in the mean field approximation. With purpose of optimisation of speech correction we developed a plane table, on which current point with co-ordinates {V-rate, V-rhythm} traces the trajectory. If this trajectory comes nearer to compact area of normal values in result of correction reception than these correcting reception admits effective and visa versa.

Conclusion.

Thus in this paper we established experimentally computed segment durations are generated in the irregular, chaotic regime for normal speech and they are generated in the fractal bifurcation oscillation regime for stuttering. It's established that the model of the considered process permits the change of dynamic regimes. In other words, the model of the rhythm permits control. For optimisation of the control with help of the exterior actions the method of current estimation of the varying values of V-temp and V-rhythm was offered.

References

1

Schuster, H.G. Deterministic chaos. An Introduction.//.Physik-Verlag. Weinheim, 1984

2

Skljkarov O.P. Speech Rhythm Elementary Theory on the Base of Physical Phenomenology. // Ref. Doctoral Thesis, St.-Petersburg State Univ, 1999, 1-32

3

Skljarov, O.P. Neurodynamical Route to Chaos and Normal Speech vs. Stuttering.// In: 2000 Int. Conf. "Control of Oscillations and Chaos'', St. Petersburg,, 2000, 449-452.

4

Skljarov O.P., Skljarova T.N., Povarova I.A. The rhythm of normal speech and stuttering Journ. of Fluency Disorders. 25, N.3, p. 225

5

Van der Maas, H.L.J., Vershure, P.F. M.J.,and Molenaar, P.C.M. A Note on Chaotic Behavior in Simple Neural Networks. // Neural Networks. 3, p.p. 119-122.

Ваши комментарии

[Головная страница]
[Конференции]
[СО РАН]

© 2001, Сибирское отделение Российской академии наук, Новосибирск
© 2001, Объединенный институт информатики СО РАН, Новосибирск
© 2001, Институт вычислительных технологий СО РАН, Новосибирск
© 2001, Институт систем информатики СО РАН, Новосибирск
© 2001, Институт математики СО РАН, Новосибирск
© 2001, Институт цитологии и генетики СО РАН, Новосибирск
© 2001, Институт вычислительной математики и математической геофизики СО РАН, Новосибирск
© 2001, Новосибирский государственный университет
Дата последней модификации Wednesday, 29-Aug-2001 18:25:56 NOVST