Модель динамики численности популяции с неперекрывающимися поколениями с половой структурой

Утюпин Ю.В.
Мирнинский политехнический институт

Аннотация:

В данной работе исследуется параметрическая модель динамики численности изолированной популяции с половой структурой с неперекрывающимися поколениями. Для дискретно-непрерывной системы изучаются динамические режимы, которые реализуются при различных значениях параметров.

In the given work the parametrical model of dynamics of number of an isolated population with a sexual structure with not overlapped generations is investigated. For a discrete-continuous system the dynamic conditions are studied which are realized at various values of parameters.

Ключевые слова: модель динамики численности популяции.

Публикация посвящена исследованию одной параметрической модели динамики численности изолированной популяции с половой структурой. В рамках модели предполагается, что рождаемость в популяции носит дискретный характер и появление особей новых генераций происходит в фиксированные моменты времени , а смертность имеет непрерывный характер: на временных интервалах $\left[ {t_k ,t_{k + 1}}\right)$ происходит только монотонное снижение численностей.

1. На отрезках времени $\left[ {t_k ,t_{k + 1}}\right)$ динамика численности популяции описывается следующей системой дифференциальных уравнений:

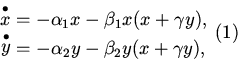
$\begin{displaymath} \begin{array}{*{20}c} {\mathop x\limits^ \bullet = - \alp... ...2 y - \beta _2 y(x + \gamma y)}, \\ \end{array} \eqno{ (1)} \end{displaymath}$

где

- численность мужских,

- численность женских особей в момент времени

. В моменты времени

появления особей новых генераций выполняются соотношения:

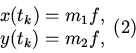
$\begin{displaymath} \begin{array}{*{20}c} {x(t_k ) = m_1 f}, \\ {y(t_k ) = m_2 f}, \\ \end{array} \eqno{(2)} \end{displaymath}$

где $f = \min \left\{ {y(t_k - 0),\varepsilon x(t_k - 0)} \right\}.$ Здесь $\alpha _1 ,\beta _1 ,\alpha _2 ,\beta _2 ,\gamma , m_1, m_2 = const > 0$ , $\varepsilon = const \geq 1$ , $t_{k + 1} - t_k = const = h > 0$ . Далее, не уменьшая общности, можно считать $\varepsilon = 1$ и

2. Непосредственно для системы (1)-(2) получены следующие результаты: - решения системы с положительными начальными данными не могут выйти за пределы 1-ой четверти; - все решения системы входят в прямоугольник $\left[ {0,\frac{{\alpha _1 (m_1 - e^{\alpha _1 } )}}{{\beta _1 (e^{\alpha _1... ...\alpha _2 (m_2 - e^{\alpha _2 } )}}{{\beta _2 (e^{\alpha _2 } - 1)}}} \right]$ и никакое решение с начальными данными в этом прямоугольнике не может выйти за его границы; этот прямоугольник существует только в случае, если выполняются условия

$\begin{displaymath} m_1 e^{ - \alpha _1 } > 1 , m_2 e^{ - \alpha _2 } > 1; \eqno{(3)} \end{displaymath}$

- точка (0,0) - стационарная точка системы (1)-(2) при любых параметрах; если одно из условий (3) не выполняется, то начало координат - глобально устойчивое состояние равновесия (то есть популяция вырождается); если же условия (3) удовлетворяются, то точка (0,0) становится неустойчивой.

3. Для дальнейшего анализа проведем некоторые преобразования. Заметим, во-первых, что в моменты выполняется соотношение

$\begin{displaymath} x(t_k ) = \frac{{m_1 }}{{m_2 }}y(t_k ), \eqno{(4)} \end{displaymath}$

и, во-вторых, система (1) имеет первый интеграл

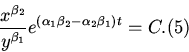
$\begin{displaymath} \frac{{x^{\beta _2 } }}{{y^{\beta _1 } }}e^{(\alpha _1 \beta _2 - \alpha _2 \beta _1 )t} = C . \eqno{(5)} \end{displaymath}$

Пользуясь соотношениями (4) и (5) можем привести модель (1) -(2) к следующему виду:

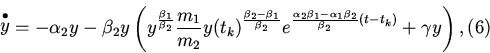
$\begin{displaymath} \mathop y\limits^ \bullet = - \alpha _2 y - \beta _2 y \le... ..._2 }}{{\beta _2 }} (t - t_k )} + \gamma y\right), \eqno{(6)} \end{displaymath}$

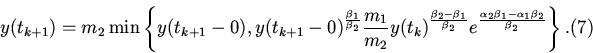
$\begin{displaymath} y(t_{k + 1} ) = m_2 \min \left\{ {y(t_{k + 1} - 0),y(t_{k +... ... - \alpha _1 \beta _2 }}{{\beta _2 }}} } \right\}. \eqno{(7)} \end{displaymath}$

Далее мы будем предполагать, что $\frac{{\beta _1}}{{\beta _2 }} < 1$ (eсли выполняется обратное неравенство, то, замечая что x и y входят в систему (1)-(2) симметрично, мы можем привести ее к виду (6)-(7) относительно x). Обозначая в (6)-(7)

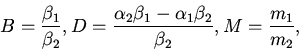
$\begin{displaymath} B = \frac{{\beta _1 }}{{\beta _2 }} , D = \frac{{\alpha _2... ...pha _1 \beta _2 }}{{\beta _2 }} , M = \frac{{m_1 }}{{m_2 }}, \end{displaymath}$

получим

$\begin{displaymath} \mathop y\limits^ \bullet = - \alpha _2 y - \beta _2 y \lef... ...t_k )^{1 - B} Me^{D(t - t_k )} + \gamma y\right ), \eqno{(8)} \end{displaymath}$

$\begin{displaymath} y(t_{k + 1} ) = m_2 \min \left\{ {y(t_{k + 1} - 0),y(t_{k + 1} - 0)^B y(t_k )^{1 - B} Me^D } \right\}. \eqno(9) \end{displaymath}$

Выражения (8), (9) представляют собой одно неавтономное уравнение с разрывами.

4. Рассмотрим уравнение (8). На каждом интервале $[t_k,t_{k+1})$ мы имеем дело с решениями задачи Коши

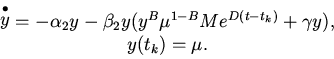
$\begin{displaymath} \begin{array}{*{20}c} \mathop y\limits^ \bullet = - \alph... ...} Me^{D(t - t_k )} + \gamma y),\\ y(t_k)=\mu. \end{array} \end{displaymath}$

Сделав здесь замену переменных $y=\mu u$ , получим задачу Коши

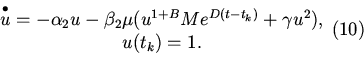
$\begin{displaymath} \begin{array}{*{20}c} \mathop u\limits^ \bullet = - \alph... ...k )} + \gamma u^2),\\ u(t_k)=1. \end{array} \eqno {(10)} \end{displaymath}$

Поскольку

, мы можем ограничить $Me^{D(t - t_k )}$ некоторой константой

. Рассмотрим две следующие задачи Коши:

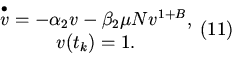
$\begin{displaymath} \begin{array}{*{20}c} \mathop v\limits^ \bullet = - \alph... ...ta _2 \mu Nv^{1+B},\\ v(t_k)=1. \end{array} \eqno {(11)} \end{displaymath}$

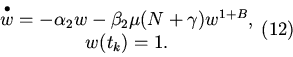
$\begin{displaymath} \begin{array}{*{20}c} \mathop w\limits^ \bullet = - \alph... ... (N+\gamma)w^{1+B},\\ w(t_k)=1. \end{array} \eqno {(12)} \end{displaymath}$

Нетрудно понять, что решение задачи Коши (10) на всем интервале $(t_k,t_{k+1})$ лежит между решениями задач Коши (11) и (12), т.е. $w<u<v \quad \forall t \in (t_k,t_{k+1})$ . Решая задачи Коши (11) и (12) и переходя к прежним переменным, получим

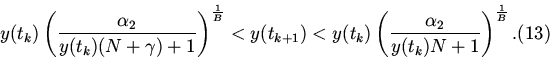
$\begin{displaymath} y(t_k)\left(\frac {\alpha _2} {y(t_k)(N+\gamma)+1}\right )... ...frac {\alpha _2} {y(t_k)N+1}\right )^\frac 1 B. \eqno {(13)} \end{displaymath}$

Уравнения

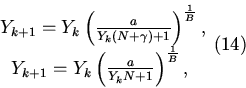
$\begin{displaymath} \begin {array}{*{20}c}Y_{k+1}=Y_k\left(\frac {a} {Y_k(N+\g... ... {a} {Y_k N+1}\right )^\frac 1 B, \ \end{array} \eqno{(14)} \end{displaymath}$

являются известными уравнениями Хассела. Известно, что для этих уравнений с увеличением параметра

возникает классическая картина бифуркаций удвоения периода, причем для обоих уравнений бифуркации происходят при одних и тех же

. Используя это, мы можем доказать следующее: - при выполнении условий (3) существует единственное нетривиальное состояние равновесия задачи (8)-(9); - если $B > \frac{1}{2}$ , то при любых других параметрах это состояние равновесия глобально устойчиво; - если $B < \frac{1}{2}$ , то с увеличением параметра

(с неизменным

) происходит бифуркация рождения цикла длины два.

5. Численный анализ показал, что при $B < \frac{1}{2}$ с дальнейшим увеличением параметра возникает классическая картина бифуркаций удвоения периода с рождением хаотических режимов.

Ваши комментарии

[Головная страница]
[Конференции]
[СО РАН]

© 2001, Сибирское отделение Российской академии наук, Новосибирск
© 2001, Объединенный институт информатики СО РАН, Новосибирск
© 2001, Институт вычислительных технологий СО РАН, Новосибирск
© 2001, Институт систем информатики СО РАН, Новосибирск
© 2001, Институт математики СО РАН, Новосибирск
© 2001, Институт цитологии и генетики СО РАН, Новосибирск
© 2001, Институт вычислительной математики и математической геофизики СО РАН, Новосибирск
© 2001, Новосибирский государственный университет
Дата последней модификации Wednesday, 05-Sep-2001 10:43:46 NOVST