
Утюпин Ю.В.
Мирнинский политехнический институт
In this article the mathematical model of a system a predator - prey is considered, in which the operation of effect of a saturation during interaction of species is taken into account. As against known model of Alekseev - Bazykin [1,2] in considered model the association of a velocity of an increase of number of predators on conditions of their feed during the defined time is taken into account. For a system of three integro-differential equations the dynamic conditions are studied which are realized at various values of parameters.
Ключевые слова: модель системы хищник - жертва.
1. Анализу математических моделей системы хищник - жертва посвящено огромное количество работ (см., например, [1-7]). Практически во всех работах рассматриваются различные модификации модели Лотки - Вольтерра [5], учитывающие в ней действие дополнительных регуляторных механизмов. В частности, в [1-4] рассматривались модификации модели Лотки - Вольтерра с "эффектом насыщения" хищников: с ростом численности жертв скорость их потребления хищниками и скорость прироста числа хищников стремились к некоторой конечной величине.
В модели Лотки - Вольтерра [5]
В модификациях [1-4] модели (1) предполагалось, что ![]() и
и
![]() не являются постоянными величинами и зависят от
значений
не являются постоянными величинами и зависят от
значений ![]() :
:
Естественно предполагать, что плодовитость особей в популяции
хищников не является постоянной и зависит от условий их питания в
течение определенного времени ![]() , т. е. зависит от величины
, т. е. зависит от величины
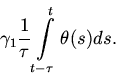
В наиболее простом случае эта зависимость является прямо
пропорциональной. Таким образом получаем уравнение:
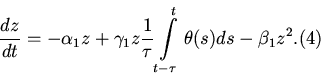
Для корректной постановки задачи требуется задание начальных
данных для функции ![]() на отрезке времени
на отрезке времени
![]() . Объединяя уравнения (2) - (4), получаем модель
системы хищник - жертва с "эффектом насыщения" с начальными
данными
. Объединяя уравнения (2) - (4), получаем модель
системы хищник - жертва с "эффектом насыщения" с начальными
данными
![]() при
при
![]() , где
, где
![]() и
и
![]() .
.
Далее, в пунктах 2-7 мы будем рассматривать модель без
саморегуляции хищника (т.е. в уравнении (4) ![]() ), а затем полную модель.
), а затем полную модель.
2. Рассмотрим модель без саморегуляции в популяции хищников.
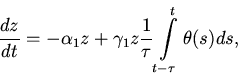
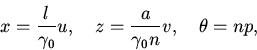
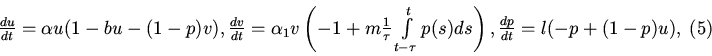
3. Учитывая то, что
Заметим, что
![]() при
при
![]() .
Следовательно, все траектории асимптотически входят в полосу
.
Следовательно, все траектории асимптотически входят в полосу
![]() и не могут выйти за ее границы, если
и не могут выйти за ее границы, если
![]() . Также выполнено неравенство
. Также выполнено неравенство
![]() . Следовательно,
. Следовательно,
![]() .
Если
.
Если ![]() , то
, то
![]() .
Таким образом, все траектории асимптотически входят в область
.
Таким образом, все траектории асимптотически входят в область
![]() .
.
Ограниченность ![]() доказывается более сложным образом (см. [10]),
но, к сожалению, только ограниченность каждой траектории, но не
ограниченность в совокупности.
доказывается более сложным образом (см. [10]),
но, к сожалению, только ограниченность каждой траектории, но не
ограниченность в совокупности.
4. Для доказательства существования и единственности решения
задачи приведем (5) к стандартному виду. Для этого примем интеграл
во втором уравнении за новую переменную ![]() , после чего с
помощью замены переменной
, после чего с
помощью замены переменной ![]() (5) приводится к виду:
(5) приводится к виду:
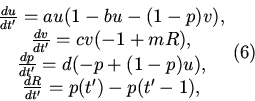
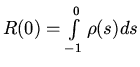 .
В результате получаем систему (6) ОДУ с запаздывающим аргументом,
для которой нетрудно показать существование и единственность
решений [10].
.
В результате получаем систему (6) ОДУ с запаздывающим аргументом,
для которой нетрудно показать существование и единственность
решений [10].
5. При любых значениях параметров система (5)
имеет две стационарные точки: ![]() и
и
![]() . Кроме того, при условии
. Кроме того, при условии ![]() в
в ![]() существует
нетривиальное равновесие
существует
нетривиальное равновесие
![]() .
.
Соответствующими стационарными точками для системы (6) будут
![]() ,
,
![]() и
и
![]() .
Исследуем эти состояния равновесия на устойчивость.
.
Исследуем эти состояния равновесия на устойчивость.
Линеаризуя (6) вблизи точки ![]() , получаем характеристическое уравнение:
, получаем характеристическое уравнение:
![]() . Поскольку это уравнение
имеет положительный корень, то, следовательно, точка
. Поскольку это уравнение
имеет положительный корень, то, следовательно, точка ![]() неустойчива.
неустойчива.
Характеристическое уравнение для точки ![]() имеет вид:
имеет вид:
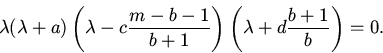
Характеристическое уравнение для точки ![]() имеет вид:
имеет вид:
![\begin{displaymath}
\lambda^2\left[\left (\lambda+\frac{ab}{m-1}\right )\left
...
...da+\frac{dm}{m-1}\right )-
\frac{ad(m-1-b)}{(m-1)^2}\right]+
\end{displaymath}](img73.gif)
6. Пусть
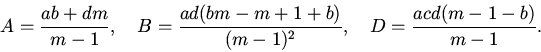
При этих обозначениях уравнение (7) примет вид:
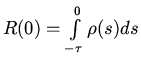 .
.
При выполнении этого условия имеется единственное нетривиальное
равновесие С. В этом случае появившийся корень ![]() не
влияет на устойчивость.
не
влияет на устойчивость.
Если все корни характеристического уравнения (8) (кроме одного нулевого) лежат слева от мнимой оси, то соответствующее решение является асимптотически устойчивым.
Справедлива следующая теорема [10]:
Теорема. Для того, чтобы все корни квазиполинома (8) (кроме
![]() ) лежали слева от мнимой оси, необходимо и достаточно,
чтобы выполнялись следующие два условия:
) лежали слева от мнимой оси, необходимо и достаточно,
чтобы выполнялись следующие два условия:
а) функция
![]() имеет на
интервале
имеет на
интервале ![]() два корня;
два корня;
б)
![]() , где
, где ![]() - корни функции
- корни функции ![]() .
.![]()
Следствие 1. Если ![]() , то не все нули квазиполинома (8)
лежат слева от мнимой оси.
, то не все нули квазиполинома (8)
лежат слева от мнимой оси.
Следствие 2. Если
![]() или
или
![]() , то
, то
![]() все нули квазиполинома (8) лежат слева от мнимой оси.
все нули квазиполинома (8) лежат слева от мнимой оси.
Следствие 3. Если одно из следующих условий не выполняется:
- функция
![]() имеет корень на
имеет корень на ![]() ,
,
- второй положительный корень функции ![]() лежит в интервале
лежит в интервале
![]() ,
,
-
![]() ,
то при
,
то при ![]() появляются корни квазиполинома (8), имеющие
положительные действительные части.
появляются корни квазиполинома (8), имеющие
положительные действительные части.
Замечание. Выполнение всех трех условий последнего следствия
не гарантирует отсутствия корней квазиполинома с положительной
действительной частью при ![]() .
.
Рассмотрим структуру плоскости параметров ![]() (рис. 1). Здесь
(рис. 1). Здесь
![]() - кривая, ограничивающая область существования корней
функции
- кривая, ограничивающая область существования корней
функции
![]() на интервале
на интервале
![]() . Она
состоит из части параболы
. Она
состоит из части параболы ![]() и части прямой
и части прямой
![]() .
.
Можно показать [10], что:
1. Если точка (B,D) лежит в области ![]() , ограниченной прямой
, ограниченной прямой
![]() , линией касания функций
, линией касания функций ![]() и
и
![]() (пунктирная линия) и прямой
(пунктирная линия) и прямой
![]() , то при любом
, то при любом
![]() не все нули квазиполинома (8) лежат слева от мнимой оси.
не все нули квазиполинома (8) лежат слева от мнимой оси.
2. Если точка ![]() принадлежит областям
принадлежит областям ![]() (рис. 2), то
при
(рис. 2), то
при ![]() все нули квазиполинома будут лежать слева от
мнимой оси. Если
все нули квазиполинома будут лежать слева от
мнимой оси. Если ![]() не принадлежит областям
не принадлежит областям ![]() , то
при
, то
при ![]() не все нули квазиполинома будут лежать слева от
мнимой оси. Если
не все нули квазиполинома будут лежать слева от
мнимой оси. Если ![]() лежит в области V (заштрихованная
область), то при
лежит в области V (заштрихованная
область), то при ![]() и при
и при ![]() не все корни
квазиполинома лежат слева от мнимой оси.
не все корни
квазиполинома лежат слева от мнимой оси.
3. Если точка ![]() принадлежит области
принадлежит области ![]() и
и
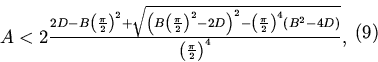
4. Если точка ![]() принадлежит области
принадлежит области ![]() и
и
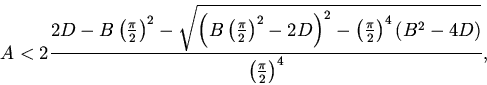
7. Анализ зависимости устойчивости нетривиального
стационарного состояния от ![]() методом D-разбиений показал [9],
что увеличение запаздывания в (5) сужает область устойчивости.
методом D-разбиений показал [9],
что увеличение запаздывания в (5) сужает область устойчивости.
Как показал анализ, в зависимости от параметров нетривиальное
состояние равновесия может быть как устойчивым, так и
неустойчивым. Предположим, что нетривиальное равновесие
неустойчиво. Тогда в ![]() не существует устойчивых стационарных
точек. Тогда из ограниченности решений системы следует, что в
фазовом пространстве должен существовать какой-либо устойчивый
аттрактор. Когда параметры лежат в области неустойчивости вблизи
бифуркационной кривой, решения "наматываются" на предельный цикл.
Как показал численный анализ, при удалении от бифуркационной
кривой предельный цикл не исчезает. Таким образом, когда параметры
лежат в области неустойчивости, в
не существует устойчивых стационарных
точек. Тогда из ограниченности решений системы следует, что в
фазовом пространстве должен существовать какой-либо устойчивый
аттрактор. Когда параметры лежат в области неустойчивости вблизи
бифуркационной кривой, решения "наматываются" на предельный цикл.
Как показал численный анализ, при удалении от бифуркационной
кривой предельный цикл не исчезает. Таким образом, когда параметры
лежат в области неустойчивости, в ![]() существует предельный
цикл.
существует предельный
цикл.
Заметим также, что на D-разбиении присутствуют области с двумя парами корней, лежащих справа от мнимой оси. В этом случае система должна иметь двухчастотные колебания. Численный эксперимент таких режимов не выявил.
8. Далее будем рассматривать полную модель, т.е. модель с
саморегуляцией в популяции хищников. С помощью той же замены
переменных, что и в пункте 2, получим следующую систему
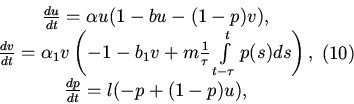
9. Также как и в п. 3 доказывается, что траектории не
выходят за границы ![]() и все траектории асимптотически входят
в область
и все траектории асимптотически входят
в область
![]() и не
могут выйти за ее границы. Кроме того, заметим, что
и не
могут выйти за ее границы. Кроме того, заметим, что
![]() при
при
![]() и при
и при
![]() на отрезке
на отрезке
![]() . Следовательно, в
. Следовательно, в ![]() существует инвариантное компактное
притягивающее множество
существует инвариантное компактное
притягивающее множество
![$[0,\frac 1 b]\times\left[0,\frac 1
{b_1}(\frac m{b+1}-1)\right]\times[0,\frac 1 {b+1}]$](img122.gif) .
.
Существование и единственность решений системы доказывается также, как и для системы без саморегуляции в популяции хищников. Кроме того, полная система имеет такие же тривиальные состояния равновесия и те же самые условия их устойчивости. Понятно, что и условия вырождения будут такими же.
10. Перейдем к исследованию нетривиальных состояний
равновесия.
Состояния равновесия удовлетворяют следующим уравнениям:
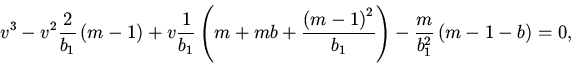
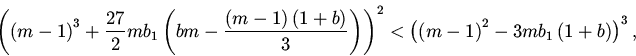
Дальнейший анализ устойчивости сводится к исследованию расположения нулей квазиполинома (11). Для этого мы, как и в пункте 7, воспользовались методом D-разбиений.
Области в пространстве параметров с различным количеством корней
квазиполинома (11), имеющих положительные вещественные части,
отделяются параметрическими гиперповерхностями
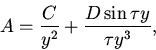
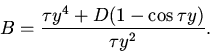
С помощью численных экспериментов были выявлены следующие режимы:
- вырождение популяции хищника;
- стабилизация на ненулевом уровне;
- одна неустойчивая стационарная точка, окруженная глобально устойчивым пределным циклом;
- три нетривиальных состояния равновесия, два из которых устойчивы;
- три нетривиальных состояния равновесия, одно из которых неустойчиво и окружено устойчивым предельным циклом.
- три нетривиальных состояния равновесия, одно из которых неустойчиво; все траектории наматываются на один аттрактор - устойчивое состояние равновесия.
Отметим, что модель Базыкина - Алексеева обладает большим количеством фазовых портретов. Но в нашей модели обнаружена только их часть. Проблема заключается в том, что уже в Модели Базыкина - Алексеева области параметров, для которых реализуются недостающие режимы, достаточно узкие. С введенем третьего уравнения и запаздывания эти области еще более сужаются или исчезают вовсе. Конечно, недостающие режимы также могут реализовываться в рамках рассматриваемой модели, но именно в тех случаях, когда мы можем перейти к самой модели Базыкина - Алексеева.
11. В работе рассмотрена модель системы "хищник - жертва" с эффектом насыщения, с саморегуляцией в популяции жертв и рождаемостью в популяции хищника, зависящей от условий их питания, и та же модель , только с саморегуляцией в популяции хищников. Для обеих моделей доказана корректность модели, т. е. существование, единственность и ограниченность решений. Найдены необходимые и достаточные условия вырождения хищника при любых начальных данных.
Показана возможность существования нетривиального равновесия (условия сосуществования видов). Анализ модели позволил выявить достаточно широкий набор динамических режимов. Проведен анализ влияния западывания на устойчивость.
 Ваши комментарии
Ваши комментарии
|
![[SBRAS]](/gif/s_sigma.gif)
[Головная страница] [Конференции] [СО РАН] |
© 2001, Сибирское отделение Российской академии наук, Новосибирск
© 2001, Объединенный институт информатики СО РАН, Новосибирск
© 2001, Институт вычислительных технологий СО РАН, Новосибирск
© 2001, Институт систем информатики СО РАН, Новосибирск
© 2001, Институт математики СО РАН, Новосибирск
© 2001, Институт цитологии и генетики СО РАН, Новосибирск
© 2001, Институт вычислительной математики и математической геофизики СО РАН, Новосибирск
© 2001, Новосибирский государственный университет
Дата последней модификации Wednesday, 05-Sep-2001 10:45:36 NOVST