Core and equilibria in nonatomic mixed economy ¹

Vasil'ev V.A.
Sobolev Institute of Mathematics of SB RAS, Novosibirsk

Abstract:

This paper is concerned with the core equivalence theorems in a model of mixed economy. An essential feature of this model is that two different regulation mechanisms function jointly: central planning and flexible market prices. To provide a characterization of equilibria in nonatomic mixed economy in terms of coalitional stability, a fuzzy-core approach, based on the classic Lyapunov Convexity Theorem, is proposed.

Работа посвящена исследованию условий совпадения неблокируемых и равновесных распределений в одной модели смешаной экономики. Отличительной чертой изучаемой модели является сосуществование (симбиоз) двух различных механизмов регулирования: рыночной конкуренции и централизованного планирования.Предлагается подход к характеризации равновесных распределений смешанной экономики в терминах коалиционой устойчивости, основанный на использовании нечетких ядер и классической теоремы А.А.Ляпунова о выпуклости множества значений неатомической векторной меры.

1. Introduction

This paper is concerned with the core equivalence theorem in a mixed economy - analogy of the famous Aumann Theorem on cooperative characterization of equilibria in the standard nonatomic pure exchange economy. Recall from [2] that nonatomicity assumption is the proper mathematical formulation of the traditional economic concept of perfect competition, implying the influence of every individual economic agent to be negligible. An essential feature of the mixed economy models, introduced in a more general context in [6], is that two different regulation mechanisms function jointly: central planning and flexible market prices. Thus, unlike the standard pure exchange models, these models are characterized by the presence of dual markets. In the first market, prices are stable and the allocation of commodities to a great extent is determined by rationing schemes and government orders. In the second market, prices are flexible and are formed by the standard market mechanism of equating demand and supply. We assume that the excess of any commodity purchased in the first market may be resold by any agent at flexible market prices.

In our investigation of the mixed economy in question, a fundamental role is played by the fact that the income functions are nonlinear as a result of multiple regulation mechanisms. A consequence thereof is an essential dependence of the type of cooperative stability on the order structure of equilibrium prices which considerably distinguishes the mixed models from the standard ones. Thus, the problem of properly defining cores in mixed economic systems arises from both the presence of fixed state prices for rationed commodities and the multiplicity of types of coalitional stability of equilibrium allocations which correspond to different types of flexible prices in the second market. A universal way to overcome the difficulties indicated is based on the use of a linear approximation of nonlinear income functions and leads to the formation of several types of cores which characterize all possible variants of coalitional stability.

In this paper we introduce the notion of the core in the model with two types of markets, described above, and present the conditions for coincidence of the core and mixed equilibrium allocations in nonatomic case. To provide a cooperative characterization of equilibria in nonatomic economies (both standard and mixed), a fuzzy-core approach, based on the classic Lyapunov Convexity Theorem [5], is proposed. By applying this approach, a proof of the core equivalence theorem in nonatomic mixed economy is given.

In the interests of saving space and clarifying the main ideas the paper deals with the convex preferences. More general treatment can be found in [7].

2. The model of mixed economy

The formal description of the mixed economy model in question is similar to that introduced in Makarov, Vasil'ev et al.[6]. One of the main differences is the infinite number of economic agents, which are presented by the measure space ${\cal{A}} = (A, \Sigma, \nu)$ , where

is a set of participants, $\Sigma$ is a $\sigma$ -algebra of their coalitions, and $\nu$ is nonatomic probabilistic measure. We assume for simplicity that production sets are trivial ( $Y(a) = \{0\}$ $\nu$ -a.e in

), and consumption sets available to the economic agents under the fixed and flexible prices are the same and equal to $R^l_{+}$ , where

is the number of commodities in the economy. Among the other distinctive features of the model is the presence of so-called governmental order $\theta :A\to R^l_+$ and state market income function $\alpha :P \times A \to R$ , specifying the governmental order $\theta (a)$ placed with the agents $a \in A$ and the gains $\alpha (p,a)$ of participants $a \in A$ when transferring the governmental orders $\theta (a)$ for the central allocation. Here and below $P=R^l_{+}$ is the set of market (flexible) prices.

From now on we use the notations and definitions given in [3] and [7]. Besides the standard characteristics of economic agents $w : A \to R_{+}^l$ and $\succ :A \to {\cal P}_{mo}$ , which describe initial endowments $w(a) \in R^l_{+}$ and irreflexive, monotone, strictly increasing on the second argument preference relations $\succ_{a}$ of agents $a \in A$ , defined on $R^l_{+} \times R^l_{+}$ (not on $R^l_{+}$ because of the presence of dual markets), the model is characterized also by the vector $q \in \mbox{int} R^l_{+}$ of fixed state prices, and the map $\beta :A \to R^l_{+}$ describing the maximum amount of rationed goods available at the fixed prices in the first market.

It is assumed that the standard hypothesis of measurability and integrability (see, for example, [2] and [3]) are fulfilled: for any (integrable w.r.t. $\nu$ ) functions $x, y \in {\cal L}_{\nu} = {\cal L}_{\nu}(R^{2l}_{+})$ it holds:

$\begin{displaymath} \{a \in A \mid x(a) \succ_{a} y(a)\} \in \Sigma, \end{displaymath}$

and $\beta, \theta, w \in {\cal L}_{\nu}(R^{l}_{+})$ , where ${\cal L}_{\nu}(E)$ is a space of all $\nu$ -integrable functions from

(

is supposed to be a subset of a finite-dimensional vector space).

As usual, we suppose that the open-graph condition is satisfied: for any $a \in A$ the graph of $\succ_{a}$ is open in $R^{2l}_{+} \times R^{2l}_{+}$ . Moreover, in order to save a space and clarify the main ideas we restrict ourselves to the case of convex preference relations: for any $a \in A$ and $x \in R^l_{+} \times R^l_{+}$ the upper contour set

$\begin{displaymath} \{ y \in R^l_{+} \times R^l_{+} \mid y \succ_{a} x \} \end{displaymath}$

is convex.

Further, we assume that the central orders do not exceed the initial endowments of the economic agents:

$\begin{displaymath} \theta(a) \leq w(a) \end{displaymath}$

for any $a \in A,$ and the rationing $\beta$ is used for reallocating the entire governmental order:

$\begin{displaymath} \int\limits \beta\,d\nu = \int\limits \theta\,d\nu \end{displaymath}$

(here and below we use the standard shortening $\int\limits f\,d\nu = \int\limits_{A} f\,d\nu$ ). Finally, as in [2] we suppose (with conventional interpretation) that $\int\limits w\,d\nu \in \mbox{int} R^l_{+}$ .

To conclude the description of the mixed economy in question

$\begin{displaymath} {\cal E} =\langle {\cal A}, \succ, \alpha, \beta, \theta, w, q\rangle, \end{displaymath}$

we fix one of its main specification ${\cal E}^q$ corresponding to the following type of the state market income function $\alpha,$ characterizing the payment $\alpha (p,a)$ of the central agency for the delivery $\theta (a)$ of obligatory supply:

$\begin{displaymath} \alpha (p,a)= q \cdot \theta (a) \end{displaymath}$

for all $a \in A$ and $p \in P.$ Observe, that under this specification the total governmental market income $\int\limits \alpha (p,\cdot)\,d\nu$ provides consumption of the maximum total amount $\int\limits \beta\,d\nu$ of rationed goods against fixed state prices

In order to give the formal definition of budget sets in the economy ${\cal E}^q,$ let us remind once more (see [6], for example) that it is assumed that in our model two markets function simultaneously. In the first (state) market, the prices are fixed at and the consumption $x^{\prime}(a) \in X^{\prime}(a) = R^l_{+}$ of each economic agent $a \in A$ is bounded above by the vector $\beta (a)$ giving the rationing on the demand for the state commodities. Furthermore, each consumer $a \in A$ is faced with a vector $\theta (a)$ of commodities which is the ``obligatory'' supply of the agent to the central agency. This means that initially consumer is obliged to deliver the amount $\theta (a)$ (which is at most equal to his initial endowment ) to the central agency. Then, the central agency redistributes the total amount $\int\limits \theta\,d\nu$ by offering for sale on the state market the bundles $\beta (a)$ to the agents $a \in A$ . All trades on the first (state) market take place against fixed prices .

In the second market, apart from purchasing any commodity vector $x^{\prime\prime}(a) \in X^{\prime\prime}(a) = R^l_{+}$ at the flexible prices $p\in R_+^l$ , the following procedure of reselling commodities purchased at the prices is allowed. If the current flexible price is higher than the fixed price , then each agent $a \in A$ purchases in the first market the maximum quantity $\beta_k(a)$ of the corresponding commodity $k \in L = \{1, \ldots, l\}$ and resells the excess (compared to the demand $x_k^{\prime}(a)$ of the agent) equal to $\beta_k(a) - x_k^{\prime}(a)$ at the free price in the second market.

Thus, the budget set of an agent $a \in A$ at the flexible prices $p \in P = R_+^l$ is defined by the formula

$\begin{displaymath} B_a^q(p)= \big\{(x^{\prime}, x^{\prime\prime}) \in X_a(\be... ...ime}+p\cdot x^{\prime\prime} \leq d_a(p, x^{\prime}) \big\}, \end{displaymath}$

where

$\begin{displaymath} X_a(\beta) =\big\{(x^{\prime},x^{\prime\prime})\in R^l_{+} \times R^l_{+} \mid x^{\prime}\leq \beta (a) \big\}, \end{displaymath}$

$\begin{displaymath} d_a(p, x^{\prime}) = q \cdot \theta(a) + p \cdot (w(a) -\theta(a))+ (p-q)^+ \cdot (\beta(a) - x^{\prime}); \end{displaymath}$

here and below, we use the common notations: $p\cdot x$ is the scalar product of vectors

and

; given $p=(p_1,\ldots, p_l)$ and $q=(q_1,\ldots, q_l)$ , the vector

has the components $(p-q)_k^+=\max\{p_k-q_k,0\}$ .

As to the demand set of the consumer $a \in A$ , it is defined in a usual manner:

$\begin{displaymath} D^q_a(p) = \big\{ x \in B_a^q(p) \mid {\cal P}_{a}^{\beta}(x) \cap B_a^q(p) = \emptyset \big\}, \end{displaymath}$

where

$\begin{displaymath} {\cal P}_{a}^{\beta}(x) = \{ \tilde{x} \in X_a(\beta) \mid \tilde{x} \succ_{a} x \}. \end{displaymath}$

3. Main results

To give the definition of a mixed economy equilibrium, put

$\begin{displaymath} X(\beta )=\{x\in {\cal L}_\nu(R^{2l}_+) \mid x^{\prime}(a) \leq \beta (a) \ \ {\nu}{\rm -a.e.}\ \rm {in \ A}\} \end{displaymath}$

and by

denote the set of attainable allocations of the mixed economy ${\cal E}^q$

$\begin{displaymath} X(A) = \{x \in X(\beta ) \mid \int\limits x^o\,d\nu = \int\limits w\,d\nu\}, \end{displaymath}$

putting here and below $x^o \in {\cal L}_\nu(R^{l}_+)$ to be the total consumption on both markets: $x^o(a)=x^{\prime}(a) + x^{\prime\prime}(a),$ for any $x = (x^{\prime}, x^{\prime\prime}) \in {\cal L}_\nu(R^{2l}_+)$ and $a \in A$ .

Definition 3.1 (Mixed economy equilibrium): An allocation $\bar{x} \in X(A)$ is a mixed economy equilibrium allocation (shortly: m-equilibrium or equilibrium allocation) of the economy ${\cal E}^q$ , if there exists a vector $\bar{p} \in P$ of market prices, such that $\bar{x}(a) \in D^q_a(\bar{p})$ $\nu$ -a.e. in . The pair $(\bar{x}, \bar{p})$ is an m-equilibrium (shortly: equilibrium) state of the economy ${\cal E}^q$ ; in addition, the price vector $\bar{p}$ is an m-equilibrium (equilibrium, for ease) price system of ${\cal E}^q$ .

Denote by the set of m-equilibrium allocations of the mixed economy ${\cal E}^q$ . The principal difficulty of cooperative characterization of the set relates to nonlinearity of the total income functions $d_a(p, x^{\prime})$ with respect to the flexible prices . To overcome this difficulty, we make use of the fact that, for the specification considered, the functions are piecewise linear and partition into several components according to the types of possible m-equilibrium prices . The subsequent analysis of cooperative stability of m-equilibrium allocations is then carried out individually for each of these components.

We now present the formal definitions. Given $K\subseteq L = \{1, \ldots, l\}$ , put

$\begin{displaymath} P_K=\big\{p\in R_+^l \mid p_k \geq q_k \ (k\in K), \ p_j\leq q_j\ (j\in J) \big\}, \end{displaymath}$

where

denotes the complement of

, i.e., $J=L\setminus K$ . The components mentioned above are the subsets of the set

which correspond to a particular type of the m-equilibrium prices classified with the help of the convex sets

$\begin{displaymath} W^q_K = \big\{x\in W^q \mid \exists\, p\in P_K : (x,p) \mbox{ is an m-equilibrium state of } \ {\cal E}^q \big\}. \end{displaymath}$

Allocations in

are called

-equilibrium allocations of the mixed economy ${\cal E}^q$ .

We turn now to the cooperative characterization of m-equilibrium allocations in ${\cal E}^q$ . Remind, that we have put $L=\{1,\dots,l\}$ , and for any subset $M \subseteq L$ and vector $z \in R^L$ denote by its projection onto subspace $R^M\times \{0\} \subseteq R^M\times R^{L\setminus M}$ . Put $\widehat{w} = w - \theta + \beta$ , $\Sigma _{+} = \{S\in \Sigma \mid \nu(S)>0\}$ .

Definition 3.2: A coalition $S \in \Sigma_{+}$ - dominates an attainable allocation $\bar{x} \in X(A)$ in ${\cal E}^q$ if there exists $x = (x^{\prime}, x^{\prime\prime}) \in X(\beta)$ such that

K1. $x(a)\succ_a\bar x(a)$ $\nu$ -a.e. in ;

K2. $\int\limits_{S} x^o_K\,d\nu\leq \int\limits_{S} \widehat w_K\,d\nu$ ;

K3. $q_{K\cup I}\cdot \int\limits_{S} x^o\,d\nu +q_{J\setminus I}\cdot \int\limits_... ... \int\limits_{S} w\,d\nu+ q_{J\setminus I}\cdot \int\limits_{S} \theta \,d\nu$ for any $I\subseteq J$ ,
where, as before, $J=L\setminus K$ and for any function $z\in {\cal L}_\nu(R^l)$ . The -core of the economy ${\cal {E}}^q$ is the set of all allocations $x\in X(A)$ that can not be -dominated by any coalition $S \in {\Sigma}_{+}$ .

Conditions (K1)-(K3) take the simplest form for : a coalition $S \in {\Sigma}_{+}$ -dominates $\bar{x} \in X(A)$ if there exist $x = (x^{\prime}, x^{\prime\prime}) \in X(\beta)$ such that

L1. $x(a)\succ_a\bar x(a)$ $\nu$ -a.e. in ;

L2. $\int\limits_{S} x^o\,d\nu\leq \int\limits_{S} \widehat w\,d\nu$ ;

L3. $q \cdot \int\limits_{S} x^o\,d\nu \leq q \cdot \int\limits_{S} w\,d\nu$ .

To clarify the relations L1-L3 let us consider the special form of the mixed economy ${\cal E}^{q}$ under

$\begin{displaymath} (E^o)~~{\cal E}^{o}=\langle {\cal A},X(\beta), \succ, \widehat{w}\rangle, \end{displaymath}$

which is similar (except the combined form of the consumption sets $X_a(\beta)$ ) to the ordinary market economy with the initial endowment $\widehat w = w -\theta + \beta$ resulting from reallocation of

through the central order $\theta$ and the rationing $\beta$ . It is clear that ${\cal E}^{o}$ can be regarded as the pure exchange economy with equal flexible prices in both markets, where the budget sets have the following form

$\begin{displaymath} B^o_a(p) = \{x \in X_a(\beta) \mid p \cdot x^o \leq p \cdot \widehat{w}(a)\} \end{displaymath}$

and m-equilibrium allocations can be treated as conventional (competitive) equilibria. In this connection relations L1 and L2 define the direct analogies of traditional domination (improvement) in the ordinary exchange models. Thus, we may consider the

-core

and the set of

-equilibrium allocations

of the (degenerate) mixed economy ${\cal E}^{o}$ as the core and equilibria of the market economy, defined by

As to the requirement that the coalition allocation $x(a), \ a \in S$ , be balanced at the prices , represented by condition L3, it reflects a specific feature of the economy ${\cal E}^q$ , the fixed prices in the first market.

In the general case, each of the $2^{\vert J\vert}$ inequalities appearing in K3, as with the case of -domination, reflects the requirement that be balanced with respect to all possible ``extreme'' realizations of flexible market prices which have the form

$\begin{displaymath} p_{K\cup I}= q_{K\cup I}, \ p_{J \setminus I}=0 \ \ (I\subseteq J). \end{displaymath}$

Here it is taken into account that, at zero flexible prices for commodities in $J\setminus I$ , the entire income of an agent $a \in A$ from selling the corresponding initial endowment $w(a)_{J\setminus I}$ consists only of the amount $q_{J \setminus I} \cdot \theta(a)$ guaranteed by the central agency.

Cooperative stability of allocations from and are characterized by the following analogies of the classic relation between the core and equilibria of a pure exchange economy.

Theorem 3.3: For any $K \subseteq L$ it holds

$\begin{displaymath} W^q_L \cup W^o_L \subseteq C^q_L, \ \ W^q_K \subseteq C^q_K, \ K\neq L. \end{displaymath}$

As to the reverse inclusions, we have the following analogy of the famous Aumann Core Equivalence Theorem [2].

Theorem 3.4: If ${\cal E}^q$ satisfies the assumption

$\begin{displaymath} \mbox{\rm (A)}~~\forall k\in L:~[\theta _k(a)>0\Rightarrow \beta_k(a)>0~~ \nu\mbox{-\rm a.e. in } A], \end{displaymath}$

then for any $K \subseteq L$ it holds

$\begin{displaymath}W^q_L\cup W^o_L= C^q_L,\quad W^q_K= C^q_K,\quad K \neq L.\end{displaymath}$

Remark. Assumption $\theta_{k}(a) > 0 \ \Rightarrow \beta_{k}(a) > 0$ may be interpreted in the following way: nonzero obligatory supply of any good makes it possible to acquire the same commodity at the state market (with the subsequent reselling in the free market).

Putting $C^q=\bigcup\limits_{K\subseteq L} C^q_K,$ and taking into account that assumption $\int\limits w\,d\nu \in \mbox{int} R^l_{+}$ guarantees the coincidence of the core and equilibria of the economy ${\cal E}^o$ (for more details see [2] and [3]), we have the following core equivalence result.

Corollary 3.5: Under the assumption (A) it holds

$\begin{displaymath} W^q\setminus W^{o}=C^q\setminus C^{o}. \end{displaymath}$

4. Fuzzy-core approach

Presented below is an outline of the fuzzy-core approach, allowing not only to give a cooperative characterization of mixed equilibrium allocations without nonatomicity assumption, but to clarify, as well, the impact of the Lyapunov Theorem [5] on the convexity of the range of nonatomic vector measure to the core equivalence result, formulated in the previous Section. So, from now on we omit nonatomicity assumption (if not explicitly assumed). To remind the standard definition of fuzzy coalition we put $F = \{\tau \in {\cal L}_{\nu}(R) \mid \tau(a) \in [0,1] \ \nu\rm {-a.e. \ in} \$ A $\}$ and denote by $F_{+}$ the set of those functions $\tau \in F$ whose supports $supp\, {\tau} = \{a \in A \mid \tau(a) > 0\}$ belong to $\Sigma_{+}$ :

$\begin{displaymath} F_{+} = \{\tau \in F \mid \nu ( supp\, {\tau}) > 0\}. \end{displaymath}$

Recall from [1] that the elements of the set $F_{+}$ are called fuzzy coalitions.

To present the notion of -fuzzy domination, for any $\varphi \in {\cal L}_{\nu}(R)$ and $z \in {\cal L}_{\nu}(R^{m})$ we will denote by ${\varphi}z$ the function ${\varphi}z(a)= \varphi(a)z(a), \ a \in A.$

Definition 4.1: A fuzzy coalition $\tau$ -dominates in ${\cal E}^q$ an allocation $\bar{x} \in X(A)$ if there exists $x \in X(\beta)$ such that

KF1. $x(a)\succ_a\bar x(a)$ $\nu$ -a.e. in ;

KF2. $\int\limits {\tau}x^o_K\,d\nu\leq \int\limits \tau\widehat w_K\,d\nu$ ;

KF3. $q_{K\cup I}\cdot \int\limits {\tau}x^o\,d\nu + q_{J \setminus I}\cdot \int\lim... ...\int\limits {\tau}w\,d\nu+ q_{J\setminus I}\cdot \int\limits \tau\theta \,d\nu$ for any $I\subseteq J$ .

The fuzzy -core of the economy ${\cal {E}}^q$ is the set $C_{K,F}^q$ of all allocations $x\in X(A)$ that can not be -dominated by any fuzzy coalition.

We have the following straightforward generalization of the Theorems 3.3 and 3.4.

Theorem 4.2: Let $\nu$ be any probabilistic measure (not necessarily nonatomic). Then for any mixed economy ${\cal {E}}^q$ with measure space of agents ${\cal{A}} = (A, \Sigma, \nu)$ and for any $K \subseteq L$ it holds

$\begin{displaymath} W^q_L \cup W^o_L \subseteq C^q_{L,F}, \ \ W^q_K \subseteq C^q_{K,F}, \ K \neq L. \end{displaymath}$

If, in addition, ${\cal {E}}^q$ satisfies the assumption (A), then for any $K \subseteq L$ it holds

$\begin{displaymath} C_{L,F}^q = W^q_L \cup W^o_L, \ \ C^q_{K,F} = W^q_K, \ \ K \neq L. \end{displaymath}$

Sketch of the proof: To establish the nontrivial inclusion $C_{K,F}^q \subseteq W_K^q$ in the most interesting situation $K \neq L, \ \emptyset$ , fix any $\bar{x} \in C_{K, F}^q$ and consider the set

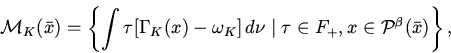
$\begin{displaymath} {\cal M}_K (\bar{x}) = \left\{\int\limits \tau[{\Gamma}_K(x... ...\mid \tau \in F_{+}, x \in {\cal P}^{\beta}(\bar x)\right\}, \end{displaymath}$

where $\Gamma _K$ is the linear operator from ${\cal L}_{\nu}(R^{2l})$ into ${\cal L}_{\nu}(R^{2l})$ acting by the rule $\Gamma _K((z^{\prime}, z^{\prime\prime}))=(z^{\prime}_J, z^o-z^{\prime}_J)$ , $\omega_K$ is the function from ${\cal L}_{\nu}(R^{2l})$ defined by the formula

$\begin{displaymath} \omega _K(a) =(\gamma(a)+\beta _J(a),\widehat w(a)-\beta _J(a)), \ a \in A, \end{displaymath}$

and

$\begin{displaymath} {\cal P}^{\beta}(\bar x) = \{x \in X(\beta) \mid x(a) {\succ}_{a} \bar{x}(a) \ \nu\rm {-a.e. \ in} \ {\it A} \}. \end{displaymath}$

From the assumption $\bar x \in C^q_{K,F}$ and directly from the definition of ${\cal M}_K(\bar x)$ it follows that ${\cal M}_K(\bar x) \cap T = \emptyset$ , where

$\begin{displaymath} T=\{(y^{\prime},y^{\prime\prime}) \in R^{2l} \mid y^{\prim... ...minus I} \cdot y^{\prime\prime} \leq 0, \ I \subseteq J\}. \end{displaymath}$

Taking into account the convexity of individual preferences ${\succ}_{a},$ it is not very hard to verify that ${\cal M}_K(\bar x)$ is a convex set. Applying the Minkovski separation theorem to the disjoint convex sets ${\cal M}_K(\bar x)$ and we get: there exists a nonzero linear functional $p=(p^{\prime},p^{\prime\prime})$ such that

$\begin{displaymath} \sup \{p \cdot y \mid y \in T\} \leq \inf \{p \cdot u \mid u \in {\cal M}_K (\bar x)\}. \end{displaymath}$

It is clear, that

is a cone. Hence, from the inequalities mentioned above we have:

belongs to the polar cone $T^o = \{z \in R^{2l} \mid z \cdot y \leq 0, \, y \in T\}$ . Since

is closed and convex, the bipolar theorem gives an equality $T=T^{oo}$ . By applying this equality it is not very hard to verify that

has the following form:

$\begin{displaymath} T^o=\{(\alpha q,p)\in R^{2l}_+\mid \alpha q_K\leq p_K,\, \alpha q_J\geq p_J, \, \alpha \geq 0\}. \end{displaymath}$

Thus, the separating functional $p=(p^{\prime},p^{\prime\prime})$ may be represented as follows: $p^{\prime} = \bar{\alpha}q, \, p^{\prime\prime}= \bar{p}$ , where $\bar{\alpha} \geq 0, \ 0 \leq {\bar{p}}_J \leq \bar{\alpha}q_J$ , and $\bar{\alpha}q_K \leq {\bar{p}}_K$ . Applying this representation and taking into account inclusions $\bar{x} \in C_{K, F}^q$ and $p \in T^o$ we obtain that $\nu$ -a.e. in

it holds

$\begin{displaymath} \bar{\alpha}q \cdot (-\gamma _K(a)+x_{J}^{\prime}-\theta_J... ...}-\widehat w(a))_K+(x^{\prime\prime}+\theta(a)-w(a))_J)\geq 0 \end{displaymath}$

whenever $x \in {\cal P}_{a}^{\beta} (\bar x(a))$ .

It is not very hard to verify that $\bar{\alpha} > 0$ (otherwise we get equality contradicting to our assumption $K \neq L, \ \emptyset$ ). Hence, because of the homogeneity of the budget constraints w.r.t. prices $(p^{\prime}, p^{\prime\prime})$ we may put $\bar{\alpha} = 1$ and to complete the proof of the inclusion $\bar x \in W^q_K$ by applying the argumentation similar to that used in [7]. Q.E.D.

Finally, to make clear the main source of the core equivalence phenomenon -- applicability of Lyapunov Convexity Theorem -- we present an equivalence theorem of a different type than previously given.

Theorem 4.3: Let $\nu$ be a nonatomic probabilistic measure. Then for any mixed economy ${\cal {E}}^q$ with agents' measure space ${\cal{A}} = (A, \Sigma, \nu)$ and for any $K \subseteq L$ it holds

$\begin{displaymath}C^q_{K,F} = C^q_K. \end{displaymath}$

Sketch of the proof: Let us establish that for any $K \subseteq L$ an inclusion $C^q_K \subseteq C^q_{K,F}$ is valid (the opposite inclusion is evident). For this end pick some $z \in X(A)$ which is dominated by a fuzzy coalition $\tau$ via some allocation $x \in {\cal P}^{\beta}(z)$ and prove that doesn't belong to the core . Consider the linear operator $E_x: \varphi \to E_x(\varphi)$ from ${\cal L}_{\nu}(R)$ into $(R^{5l})$ acting by the rule

$\begin{displaymath} E_x(\varphi)= \left(\int {\varphi}x^{\prime}\,d\nu, \int {... ...phi} {\widehat{w}}_K\,d\nu,\int \varphi\theta\,d\nu \right). \end{displaymath}$

Applying the same argumentation as in the Lindenstrauss' proof of the Lyapunov Convexity Theorem (see [4]) we get the equality

where $F_o = \{\chi_{T} \mid T \in \Sigma \}$ is the set of indicator functions $\chi_{T}$ of the standard coalitions $T \in \Sigma$ . Hence, there exists a coalition $S \in \Sigma$ such that $E_x(\tau) = E_x(\chi_S).$ From here, by definition of the linear operator

it follows: coalition

-dominates the allocation

, which means that $z\notin C^q_K$ . Q.E.D.

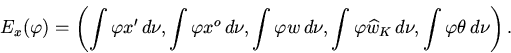
To conclude, observe, that the coincidence of the core and equilibrium allocations in nonatomic mixed economy ${\cal E}^q$ (Theorem 3.4) follows immediately from Theorems 4.2 and 4.3.

Bibliography

1: Aubin J.-P. Mathematical Methods of Game and Economic Theory. Amsterdam-New York-Oxford: North-Holland, 1979.
2: Aumann R.J. Markets with a continuum of traders //Econometrica, 32, 1964, 39-50.
3: Hildenbrand W. Core and Equilibria of a Large Economy. Princeton, NJ: Princeton University Press, 1974.
4: Lindenstrauss J. A short proof of Liapunoff's Convexity Theorem // Journal of Mathematics and Mechanics, 15, 1966, 971-972.
5: Lyapunov A.A. On completely additive vector-functions // Izve stija Akademii Nauk SSSR, 4, 1940, 465-478 (Russian).
6: Makarov V.L., V.A. Vasil'ev, et al. On some problems and results of modern mathematical economics // Optimization, 1982, 30, 5-86 (Russian).
7: Vasil'ev V.A. Core equivalence in a mixed economy // In: ``The Theory of Markets'', Amsterdam-Oxford-New York-Tokyo: North-Holland, 1999, 59-82.

Footnotes

... economy ¹: Financial support from the Russian Fund of Basic Research (grant 00-15-98884) and Russian Humanitarian Scientific Fund (grant 99-02-00141) is greatfully acknowledged

Ваши комментарии

[Головная страница]
[Конференции]
[СО РАН]

© 2001, Сибирское отделение Российской академии наук, Новосибирск
© 2001, Объединенный институт информатики СО РАН, Новосибирск
© 2001, Институт вычислительных технологий СО РАН, Новосибирск
© 2001, Институт систем информатики СО РАН, Новосибирск
© 2001, Институт математики СО РАН, Новосибирск
© 2001, Институт цитологии и генетики СО РАН, Новосибирск
© 2001, Институт вычислительной математики и математической геофизики СО РАН, Новосибирск
© 2001, Новосибирский государственный университет
Дата последней модификации Tuesday, 11-Sep-2001 15:23:31 NOVST

Core and equilibria in nonatomic mixed economy 1

Abstract:

Bibliography

Footnotes

Core and equilibria in nonatomic mixed economy ¹