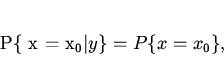 |
(1) |

Семенов А.А.
Институт динамики систем и теории управления СО РАН, Иркутск.
где ![]() -оценка открытого текста, выбираемая из множества открытых текстов
-оценка открытого текста, выбираемая из множества открытых текстов
![]() ,
, ![]() - истинный открытый текст,
- истинный открытый текст, ![]() - криптограмма, являющаяся
элементом множества криптограмм
- криптограмма, являющаяся
элементом множества криптограмм ![]() . Важнейшим результатом работы [3] стало
доказательство совершенной секретности некоторых известных типов шифров,
простейшим из которых является шифр Вернама. Однако там же было показано,
что в рамках общепринятых (на момент 1949 г.) концепций шифрования
совершенно секретные системы непрактичны, поскольку условие (1) влечет за
собой необходимость передавать по секретному каналу не меньший объем
информации, чем по открытому. Таким образом, неявно была поставлена задача
построения практичных криптосистем, в которых возможна передача большого
объема шифртекста (по отношению к объему информации, переданной по
секретному каналу) с сохранением совершенной секретности.
. Важнейшим результатом работы [3] стало
доказательство совершенной секретности некоторых известных типов шифров,
простейшим из которых является шифр Вернама. Однако там же было показано,
что в рамках общепринятых (на момент 1949 г.) концепций шифрования
совершенно секретные системы непрактичны, поскольку условие (1) влечет за
собой необходимость передавать по секретному каналу не меньший объем
информации, чем по открытому. Таким образом, неявно была поставлена задача
построения практичных криптосистем, в которых возможна передача большого
объема шифртекста (по отношению к объему информации, переданной по
секретному каналу) с сохранением совершенной секретности.
В представляемой работе предлагается подход к решению данной проблемы. В
разделе II описывается общая конструкция криптосистемы, базовыми объектами
которой являются линейные векторные пространства над произвольным полем.
Показывается, что в случае конечных полей ![]() (
(![]() -
простое число, либо натуральная степень простого числа) в рамках
криптосистемы возможно породить
-
простое число, либо натуральная степень простого числа) в рамках
криптосистемы возможно породить
![]() (
(![]() ) криптограмм, обладающих
совершенной секретностью с
вероятностью, отличной от единицы на произвольную (наперед заданную) малую
константу (относительно дискретной
вероятностной меры). При этом по секретному каналу передается не более
) криптограмм, обладающих
совершенной секретностью с
вероятностью, отличной от единицы на произвольную (наперед заданную) малую
константу (относительно дискретной
вероятностной меры). При этом по секретному каналу передается не более
![]() бит
секретной информации (где
бит
секретной информации (где ![]() - размерность векторного пространства над
- размерность векторного пространства над
![]() ,
, ![]() - четное число).
- четное число).
Конструкция криптосистемы допускает абстрактное обобщение на бесконечные
поля и, в частности, на ![]() .
.
Пусть ![]() - четное. Отправитель строит две прямоугольные матрицы
- четное. Отправитель строит две прямоугольные матрицы ![]() размерности
размерности
![]() с компонентами из
с компонентами из ![]() .
Матрицы выбираются таким образом, что каждая из них имеет ранг, равный
.
Матрицы выбираются таким образом, что каждая из них имеет ранг, равный
![]() , и матрица
, и матрица ![]() (построенная в результате
конкатенации
(построенная в результате
конкатенации ![]() и
и ![]() ) является невырожденной:
) является невырожденной: ![]() (несложно
заметить, что такие матрицы всегда существуют).
(несложно
заметить, что такие матрицы всегда существуют).
Выбирается вектор
![]() , такой, что система
, такой, что система
совместна (несколько "экзотическая" запись умножения в (2) применяется лишь из соображений экономии).
Матрицу ![]() отправитель публикует, матрица
отправитель публикует, матрица ![]() и вектор
и вектор ![]() отправляются по секретному каналу получателю.
отправляются по секретному каналу получателю.
Теперь описываем процедуру порождения криптограмм. Отправитель формирует
вектор
![]() , являющийся некоторым произвольным
образом выбранным решением системы линейных уравнений (2).
Происходит это следующим образом. Фиксируется некоторая нумерация
, являющийся некоторым произвольным
образом выбранным решением системы линейных уравнений (2).
Происходит это следующим образом. Фиксируется некоторая нумерация
![]() , (
, (
![]() ) свободных переменных (система линейных уравнений, полученная после
подстановки произвольного набора значений свободных переменных, должна
иметь единственное решение). Значения свободных переменных при решении
системы (2) выбираются случайно и независимо друг от друга из поля
) свободных переменных (система линейных уравнений, полученная после
подстановки произвольного набора значений свободных переменных, должна
иметь единственное решение). Значения свободных переменных при решении
системы (2) выбираются случайно и независимо друг от друга из поля
![]() .
.
Считаем, что номера свободных переменных известны отправителю и получателю.
Обозначим свободные переменные в векторе ![]() следующим образом:
следующим образом:
![]()
Вектор открытого текста --
![]() .
Шифрующее преобразование -- покомпонентное применение
аддитивной операции поля
.
Шифрующее преобразование -- покомпонентное применение
аддитивной операции поля ![]() к векторам
к векторам
![]() и
и ![]() , где компоненты вектора
, где компоненты вектора ![]() с
номерами
с
номерами
![]() (назовем их информационными) есть скаляры
(назовем их информационными) есть скаляры
![]() , а остальные компоненты (избыточные) выбираются из
, а остальные компоненты (избыточные) выбираются из
![]() случайно и независимо друг от друга.
случайно и независимо друг от друга.
В открытый канал отправляется вектор
![]() и
собственно криптограмма - вектор
и
собственно криптограмма - вектор
![]() ,
составленный из покомпонентных сумм
,
составленный из покомпонентных сумм
![]() . Последовательность компонент
. Последовательность компонент
![]() криптограммы
криптограммы ![]() назовем информационным блоком
криптограммы, оставшиеся компоненты образуют избыточный блок.
назовем информационным блоком
криптограммы, оставшиеся компоненты образуют избыточный блок.
На приемном конце получатель строит вектор
![]() (конкатенация), матрица
(конкатенация), матрица ![]() ему известна. Таким
образом, получатель имеет в своем распоряжении систему
ему известна. Таким
образом, получатель имеет в своем распоряжении систему
которая однозначно разрешима относительно вектора ![]() . Выбирая из
полученного таким образом вектора
. Выбирая из
полученного таким образом вектора ![]() и вектора
и вектора ![]() компоненты
с номерами
компоненты
с номерами
![]() и осуществляя обратное преобразование,
получатель находит вектор открытого текста
и осуществляя обратное преобразование,
получатель находит вектор открытого текста ![]() .
.
Криптоаналитик, перехватывающий векторы
![]() и знающий
матрицу
и знающий
матрицу ![]() , оказывается перед необходимостью выбора фиксированного
отправителем решения системы
, оказывается перед необходимостью выбора фиксированного
отправителем решения системы
![]() . Однако множество
решений последней образует плоскость размерности
. Однако множество
решений последней образует плоскость размерности
![]() (
(![]() -плоскость) в евклидовой геометрии
-плоскость) в евклидовой геометрии
![]() (определение и основные свойства конечных
геометрий можно найти, например, в [2]). Таким образом, криптоаналитик
оказывается перед задачей выбора фиксированной отправителем точки из
наблюдаемой им некоторой
(определение и основные свойства конечных
геометрий можно найти, например, в [2]). Таким образом, криптоаналитик
оказывается перед задачей выбора фиксированной отправителем точки из
наблюдаемой им некоторой ![]() - плоскости в
- плоскости в
![]() .
.
Ниже будет определен класс матриц, удовлетворяющих всем оговоренным
условиям, таких, что свободные переменные в системе
![]() имеют ту же нумерацию, что и в системе
имеют ту же нумерацию, что и в системе
![]() и при этом
и при этом
Теперь предположим, что построенная криптосистема используется для
многократной передачи секретных данных при фиксированных ![]() . В
результате криптоаналитик располагает последовательностями векторов:
. В
результате криптоаналитик располагает последовательностями векторов:
![]() и
и
![]() .
.
Заметим, что в силу конструкции системы при попарно различных векторах
![]() векторы
векторы
![]() также попарно различны (предположив, что
также попарно различны (предположив, что
![]() и при
этом
и при
этом
![]() , получим, что система линейных
уравнений
, получим, что система линейных
уравнений
![]() имеет два различных решения, притом,
что
имеет два различных решения, притом,
что ![]() ). Откуда сразу следует, что наблюдая различные векторы
). Откуда сразу следует, что наблюдая различные векторы
![]() , криптоаналитик наблюдает непересекающиеся
, криптоаналитик наблюдает непересекающиеся
![]() - плоскости в
- плоскости в
![]() . Действительно, предположив, что
пара плоскостей (с номерами
. Действительно, предположив, что
пара плоскостей (с номерами ![]() и
и ![]() ) пересекается, получим, что
существует хотя бы одно общее решение
) пересекается, получим, что
существует хотя бы одно общее решение
Если же секретные ключи (
![]() ) повторяются, то
повторяются и соответствующие им векторы (
) повторяются, то
повторяются и соответствующие им векторы (
![]() ) и
этот факт становится доступным криптоаналитику (таким образом, он знает,
какие участки открытого текста зашифрованы одним и тем же секретным
ключом).
) и
этот факт становится доступным криптоаналитику (таким образом, он знает,
какие участки открытого текста зашифрованы одним и тем же секретным
ключом).
Результатом, резюмирующим свойства построенной криптосистемы, является следующая теорема.
Теорема 1.
Предположим, что для любого четного ![]() существуют
матрицы
существуют
матрицы ![]() размерности
размерности
![]() , такие, что выполнены следующие
условия:
, такие, что выполнены следующие
условия:
1.
![]() ,
,
![]() (
(![]() назовем
размерностью криптосистемы),
назовем
размерностью криптосистемы),
2. нумерации свободных переменных в произвольных совместных
системах
![]() совпадают.
совпадают.
Тогда можно указать такой способ генерации последовательности
секретных ключей
![]() и такой способ
порождения избыточных компонент в последовательности
и такой способ
порождения избыточных компонент в последовательности
![]() (для произвольного
(для произвольного ![]() ), что для любой наперед
заданной константы
), что для любой наперед
заданной константы
![]() найдется
константа
найдется
константа
![]() , такая, что для
всех
, такая, что для
всех ![]() (начиная с некоторого
(начиная с некоторого ![]() ) в криптосистеме
описанного типа (с фиксированными
) в криптосистеме
описанного типа (с фиксированными ![]() ) размерности
) размерности
![]() каждая из криптограмм
каждая из криптограмм
![]() с вероятностью
с вероятностью
![]() обладает совершенной секретностью.
обладает совершенной секретностью.
Доказательство.
Опишем общую схему порождения последовательности секретных ключей и
последовательности избыточных блоков исходных сообщений. Обозначим
Предположим, что в векторах
и
последовательность:
есть последовательность элементов поля ![]() , выбранных случайно и
независимо друг от друга.
, выбранных случайно и
независимо друг от друга.
Стандартное допущение состоит в том, что сообщение ![]() выбирается из
выбирается из ![]() случайно и, таким образом, для криптоаналитика
случайно и, таким образом, для криптоаналитика
Если предположить, что при конструировании последовательности (3) с
соблюдением всех перечисленных требований для некоторого ![]() среди
векторов
среди
векторов
![]() нет повторяющихся, то все
нет повторяющихся, то все
![]() -плоскости в
-плоскости в
![]() , доступные криптоаналитику в
результате наблюдения векторов
, доступные криптоаналитику в
результате наблюдения векторов
![]() ,
оказываются непересекающимися. Последнее означает, что для любого
,
оказываются непересекающимися. Последнее означает, что для любого
![]() (зная матрицу
(зная матрицу ![]() ) криптоаналитик должен верно выбрать
) криптоаналитик должен верно выбрать
![]() из
из ![]() равновозможных альтернатив (иными словами,
случай непересекающихся
равновозможных альтернатив (иными словами,
случай непересекающихся ![]() -плоскостей не дает криптоаналитику никакой
дополнительной информации о секретных ключах за исключением того, что все
они различны).
-плоскостей не дает криптоаналитику никакой
дополнительной информации о секретных ключах за исключением того, что все
они различны).
В силу конструкции последовательности (3) информационный и избыточный блоки
произвольной криптограммы ![]() статистически независимы. Откуда
получаем, что если среди
статистически независимы. Откуда
получаем, что если среди
![]() нет одинаковых,
то для
нет одинаковых,
то для
![]()
Последнее соотношение, в силу того, что ![]() образует группу
относительно покомпонентного сложения векторов, дает: для любого
образует группу
относительно покомпонентного сложения векторов, дает: для любого
![]() справедливо (с учетом (4)):
справедливо (с учетом (4)):
Проанализируем ситуацию с возникновением в последовательности
![]() (которая строится согласно описанной выше схеме)
повторяющихся элементов. Обозначим последовательность информационных
компонент векторов
(которая строится согласно описанной выше схеме)
повторяющихся элементов. Обозначим последовательность информационных
компонент векторов
![]() следующим образом
следующим образом
Зафиксируем первые ![]() компонент последовательности
компонент последовательности ![]() , то есть
вектор
, то есть
вектор
![]() . Всего
существует
. Всего
существует ![]() различных векторов над
различных векторов над
![]() длины
длины
![]() . Задачу о повторном появлении вектора
. Задачу о повторном появлении вектора ![]() в
последовательности (5) можно поставить в контексте следующей
классической вероятностной задачи. Рассматривается процесс, на каждом
шаге которого осуществляется случайная выборка с возвращением из
генеральной совокупности объема
в
последовательности (5) можно поставить в контексте следующей
классической вероятностной задачи. Рассматривается процесс, на каждом
шаге которого осуществляется случайная выборка с возвращением из
генеральной совокупности объема ![]() , каждый элемент выбирается с
равной вероятностью (равной
, каждый элемент выбирается с
равной вероятностью (равной
![]() ),
), ![]() -
элемент, выбранный на
-
элемент, выбранный на ![]() -том шаге. Процесс прекращается, как только в
последовательности из
-том шаге. Процесс прекращается, как только в
последовательности из ![]() выбранных элементов
выбранных элементов
![]() .
Какова вероятность
.
Какова вероятность ![]() того, что процесс продолжится после
того, что процесс продолжится после ![]() -того
шага? Хорошо известно (см. [5]), что
-того
шага? Хорошо известно (см. [5]), что
Для некоторого фиксированного
![]() запишем следующее условие:
запишем следующее условие:
где
![]() , смысл которого очевиден
(если предположить, что
, смысл которого очевиден
(если предположить, что
![]() , где
, где
![]() с ростом
с ростом ![]() , то
, то ![]() ).
).
При достаточно больших ![]() получаем приблизительную оценку для
получаем приблизительную оценку для
![]() :
:
Вывод, который можно сделать из сказанного очень важен: передав однократно по секретному каналу малое количество информации можно передать по открытому каналу экспоненциальный от размерности криптосистемы (или от количества информационных символов) объем шифртекста, причем каждая передаваемая криптограмма с вероятностью, отличающейся от единицы на заранее заданную малую константу, будет совершенно секретной. Доказательство теоремы окончено.
Замечание. Если в описанной схеме по открытому каналу передаются
только векторы
![]() , то схема представляется
собой протокол обмена между двумя пользователями "почти" случайной (в
оговоренном выше смысле) последовательностью элементов поля
, то схема представляется
собой протокол обмена между двумя пользователями "почти" случайной (в
оговоренном выше смысле) последовательностью элементов поля
![]() .
.
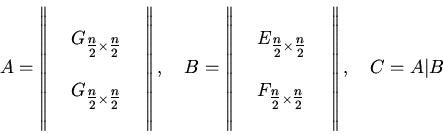
где ![]() - невырожденные над
- невырожденные над ![]() квадратные матрицы размерности
квадратные матрицы размерности
![]() ).
Дополнительно необходимо потребовать, чтобы матрицы
).
Дополнительно необходимо потребовать, чтобы матрицы ![]() и
и ![]() имели
"случайную структуру".
имели
"случайную структуру".
Например в качестве ![]() и
и ![]() можно рассматривать верхнетреугольные матрицы
с элементами из
можно рассматривать верхнетреугольные матрицы
с элементами из ![]() (на главной диагонали стоят ненулевые
элементы поля) или произведения таких матриц.
(на главной диагонали стоят ненулевые
элементы поля) или произведения таких матриц.
Совершенно очевидно, что описанную выше конструкцию можно перенести и на
бесконечные тела и, в частности, на ![]() . В данном случае множества решений
вырожденных систем линейных уравнений типа
. В данном случае множества решений
вырожденных систем линейных уравнений типа
![]() представляют собой "плоскости" в
представляют собой "плоскости" в ![]() размерности
размерности
![]() (такие "плоскости" являются смежными классами векторов
(такие "плоскости" являются смежными классами векторов
![]() , таких, что
, таких, что
![]() по подпространству решений системы
по подпространству решений системы ![]() , которое, в свою очередь,
изоморфно
, которое, в свою очередь,
изоморфно
![]() ).
).
На каждой плоскости вводится полная лебегова мера, имеющая смысл площади
любой измеримой по Лебегу области рассматриваемой плоскости. Такая мера в
общем случае ![]() -конечна (и
-конечна (и ![]() -аддитивна) и от нее можно при
помощи стандартных конструкций перейти к вероятностной мере.
-аддитивна) и от нее можно при
помощи стандартных конструкций перейти к вероятностной мере.
Каждый фиксированный открытый текст (вектор из ![]() ) представлен на
соответствующей плоскости некоторой точкой и имеет нулевую меру, таким
образом,
) представлен на
соответствующей плоскости некоторой точкой и имеет нулевую меру, таким
образом,
более того, нетрудно видеть, что событие "в последовательности
![]() есть совпадающие элементы" имеет нулевую вероятность
(каждый вектор
есть совпадающие элементы" имеет нулевую вероятность
(каждый вектор ![]() данной последовательности получается в
результате
данной последовательности получается в
результате
![]() кратного "случайного бросания"
точки на числовую прямую
кратного "случайного бросания"
точки на числовую прямую ![]() ). Таким образом, все плоскости почти
наверное различны и в силу тех же причин, что и для дискретного случая не
пересекаются. Применяя схему порождения секретных ключей и избыточных
символов в векторах открытого текста, аналогичную описанной выше, получим
самый сильный вариант совершенной секретности:
). Таким образом, все плоскости почти
наверное различны и в силу тех же причин, что и для дискретного случая не
пересекаются. Применяя схему порождения секретных ключей и избыточных
символов в векторах открытого текста, аналогичную описанной выше, получим
самый сильный вариант совершенной секретности:
(в тех же терминах). В данном контексте можно говорить о том, что криптоаналитик, располагая даже счетным множеством шифртекста, оказывается в положении, в котором он вынужден решать некоторую "вырожденную задачу".
Приведенная конструкция по сути означает, что можно говорить о криптосистемах, в которых секретность (наилучшая возможная при рассмотрении объектов над бесконечными телами и совершенная секретность для конечных полей) достигается за счет передачи избыточной информации.
Последний тезис можно несколько развить. Снова рассматриваем случай поля
![]() . Отношение
. Отношение
![]() , где
, где ![]() - общее число символов в передаваемом по открытому каналу
сообщении, а
- общее число символов в передаваемом по открытому каналу
сообщении, а ![]() - число информационных символов, назовем избыточностью
криптосистемы. Обозначим через
- число информационных символов, назовем избыточностью
криптосистемы. Обозначим через ![]() -общий объем символов (например,
бит), передаваемый для организации криптосистемы по секретному каналу,
-общий объем символов (например,
бит), передаваемый для организации криптосистемы по секретному каналу,
![]() - общий объем символов (бит), составляющих пространство ключей,
которое можно сформировать, используя один раз секретный канал для
передачи
- общий объем символов (бит), составляющих пространство ключей,
которое можно сформировать, используя один раз секретный канал для
передачи ![]() символов так, чтобы каждая криптограмма оставалась
совершенно секретной (с вероятностью, отличающейся от 1 на заданную малую
(быть может нулевую) константу
символов так, чтобы каждая криптограмма оставалась
совершенно секретной (с вероятностью, отличающейся от 1 на заданную малую
(быть может нулевую) константу ![]() ), тогда можно определить
величину
), тогда можно определить
величину
![]() -
коэффициент практичности криптосистемы. Очевидно, что для криптосистемы
Вернама (непрактичной)
-
коэффициент практичности криптосистемы. Очевидно, что для криптосистемы
Вернама (непрактичной)
![]() (в криптосистеме Вернама
(в криптосистеме Вернама
![]() ).
).
Следующее утверждение (с учетом сделанных замечаний) фактически является следствием теоремы 1.
Теорема 2.
Для любого натурального ![]() можно построить
криптосистему описанного типа над полем
можно построить
криптосистему описанного типа над полем
![]() ,
такую, что:
,
такую, что:
1. криптосистема избыточна с ![]() ,
,
2. существует такая константа ![]() ,
что передав однократно по секретному каналу
,
что передав однократно по секретному каналу
бит секретной информации, можно передать по открытому каналу
бит шифртекста, при
этом каждая из
![]() криптограмм с вероятностью отличной от 1 на заранее заданную малую константу
является совершенно секретной (
криптограмм с вероятностью отличной от 1 на заранее заданную малую константу
является совершенно секретной (![]() ).
).
Первый пункт очевиден. Относительно справедливости второго достаточно
заметить, что при произвольной разумной схеме кодирования каждый элемент
поля ![]() кодируется не более, чем
кодируется не более, чем ![]() битами двоичного
кода.
битами двоичного
кода.
Различные криптосистемы можно сравнивать по параметру ![]() . Например,
если для двух криптосистем (1 и 2) имеет место
. Например,
если для двух криптосистем (1 и 2) имеет место
то про
криптосистему 2 можно сказать, что она асимптотически более практичная, чем
1. Каждой константе ![]() поставим в соответствие
величину
поставим в соответствие
величину
![]() как показатель
практичности некоторой "идеальной" криптосистемы
как показатель
практичности некоторой "идеальной" криптосистемы
![]() над
полем
над
полем ![]() , у такой криптосистемы открытый текст состоит
из
, у такой криптосистемы открытый текст состоит
из ![]() символов поля (количество информационных символов).
символов поля (количество информационных символов).
Для произвольной криптосистемы ![]() над
над ![]() , у
которой количество информационных символов есть
, у
которой количество информационных символов есть ![]() введем функцию сравнения
введем функцию сравнения
для
![]() .
.
Следующее определение согласуется с принятыми парадигмами теории вычислительной сложности (см. [1]).
Определение.
По определению криптосистема ![]() считается
эффективной, если
считается
эффективной, если
![]() , такая, что
, такая, что
где ![]() - некоторый полином и
неэффективной, в противном случае (то есть когда
- некоторый полином и
неэффективной, в противном случае (то есть когда
![]()
![]() )
)
Для эффективных криптосистем эффективность тем выше, чем ниже
степень соответствующего полинома ![]() .
.
Для криптосистемы, предложенной в данной работе,
![]() , такая, что имеет место (6) и при этом
, такая, что имеет место (6) и при этом
![]() , поэтому ее можно считать очень
эффективной.
, поэтому ее можно считать очень
эффективной.
 Ваши комментарии
Ваши комментарии
|
![[SBRAS]](/gif/s_sigma.gif)
[Головная страница] [Конференции] [СО РАН] |
© 2001, Сибирское отделение Российской академии наук, Новосибирск
© 2001, Объединенный институт информатики СО РАН, Новосибирск
© 2001, Институт вычислительных технологий СО РАН, Новосибирск
© 2001, Институт систем информатики СО РАН, Новосибирск
© 2001, Институт математики СО РАН, Новосибирск
© 2001, Институт цитологии и генетики СО РАН, Новосибирск
© 2001, Институт вычислительной математики и математической геофизики СО РАН, Новосибирск
© 2001, Новосибирский государственный университет
Дата последней модификации Tuesday, 14-Aug-2001 21:21:28 NOVST