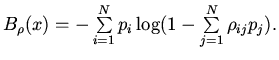О геометрическом обобщении энтропии

Леус В.А.
Институт математики им. С.Л. Соболева СО РАН

Аннотация:

Предложен новый подход к понятию вероятностного пространства. Стохастически измеримое пространство снабжается геометрической структурой путем введения расстояния между элементарными событиями. Вероятностное пространство близости используется для обобщения понятия энтропии. Показано, что геометризованная таким образом энтропия сохраняет все прежние свойства и вместе с тем приобретает неизвестную до сих пор полезную особенность. Это открывает новые возможности в области информационных дисциплин.

A new approach to the notion about a probability space is suggested. The stochastic measure space is supplied with a geometric structure by means of determination the distance between elementary events. The probabilistic proximity space is used to generalize the entropy. The so made geometrical entropy is shown to have all former properties remained and at the same time to gain some useful unknown one. This leds to the new potentialities in the realm of information sciences.

Восходящее к Л.Больцману понятие энтропии вероятностного ансамбля из исходов с вероятностями, соответственно, ( $i\in \{1,2,... ,N\}$ ) не учитывает сходства - различия между исходами. В докладе предложено обобщение, позволяющее учитывать индивидуальные особенности исходов благодаря явно содержащемуся количественному критерию близости в виде рандомизированного расстояния -- неотрицательной вещественнозначной функции $\rho_{ij}=\rho(x_{i},x_{j})\,,$ заданной на декартовом квадрате множества исходов и ограниченной сверху единицей. 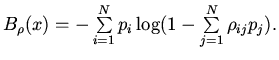Геометризованная энтропия имеет вид: $B_{\rho}(x)=-\sum\limits_{i=1}^{N} p_{i}\log (1-\sum\limits_{j=1}^{N}\rho_{ij}p_{j}).$ Введенная таким образом геометризованная энтропия обладает свойством единственности и подчиняется аддитивному закону при умножении нескольких вероятностных ансамблей. Геометризованная энтропия переходит в шенноновскую в пределе при устремлении всех $\rho_{ij},$ где $i\ne j,$ к единице.

Определение и теорема единственности

Понятие энтропии и сам термин впервые были введены физиком Л.Больцманом в конце XIX века в связи с потребностями термодинамики. В 1928 году Р.Хартли предложил в качестве меры неопределенности выбора из возможностей аналогичную больцмановской энтропии величину $H=-\log_{2}N.$ Двумя десятилетиями позже К.Шеннон следующим образом обобщил это понятие.

Пусть имеется дискретный вероятностный ансамбль с основным множеством взаимоисключающих исходов (элементарных событий) $x_{i}, i \in \{1,2,...\; M\}$ с соответствующими вероятностями Энтропией по К.Шеннону вероятностного ансамбля называется (см. например [2]) математическое ожидание случайной величины $-\log p_{i}:$

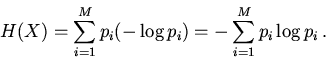
$\begin{displaymath}H(X)=\sum \limits_{i=1}^{M} p_{i} (-\log p_i)= -\sum \limits_{i=1}^{M} p_{i} \log p_i\,.\end{displaymath}$

Ясно, что энтропия по Р.Хартли является частным случаем шенноновской при равновероятных исходах.

Энтропия является априорной мерой неопределенности выбора для данного вероятностного ансамбля и лежит в основе количественного измерения информации. В [2] говорится: "информация определяется только вероятностными свойствами сообщений. Все другие их свойства, например полезность для тех или других действий, принадлежность тому или иному автору и пр., игнорируются". Известна попытка изменения этой ситуации [1]. Целью настоящей работы является развитие высказанной в [3] "геометрической" идеи такого обобщения понятия энтропии, которое позволило бы содержательно учитывать индивидуальные особенности исходов.

Кроме "рандомизированной" меры введем на основном множестве вероятностного ансамбля еще и "рандомизированное" расстояние $\rho$ как симметричную неотрицательную вещественнозначную функцию от пар исходов, ограниченную сверху единицей:

$\begin{displaymath}0 \leq \rho(x_{i},\,x_{j})=\rho_{ij} \leq 1\,.\end{displaymath}$

В дальнейшем будем говорить просто о расстоянии, опуская слово "рандомизированное". В качестве априорной меры неопределенности дискретного вероятностного ансамбля с расстоянием примем геометризованную энтропию, определяемую формулой

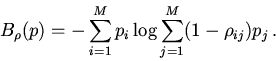$\begin{displaymath} B_{\rho}(p)=-\sum \limits_{i=1}^{M} p_{i} \log\sum\limits_{j=1}^{M} (1-\rho_{ij}) p_j\,. \end{displaymath}$

(1)

Обозначим буквой алгебру подмножеств основного множества и, понимая как принято под аддитивную меру на этой алгебре, далее под дискретным вероятностным ансамблем с расстоянием будем понимать четверку $(X,A,p,\rho)$ . Для обозначения его будем использовать ту же букву, которая обозначает основное множество, причем из контекста всегда будет ясно о чем именно идет речь. Пусть на основном множестве определены расстояние $\rho$ и расстояние $\zeta.$

Теорема 1. Если $B_{\rho}(p)=B_{\zeta}(p)$ для $\forall p,$ то $\rho \equiv \zeta.$

Доказательство проводится "от противного". Предположим, что заключение в утверждении теоремы неверно, т.е. $\rho \not\equiv \zeta.$ Тогда найдутся хотя бы два различных исхода $x_{1},\, x_{2} \in X$ такие, что $\rho(x_{1},\,x_{2})=\rho_{12}\neq \zeta_{12}=\zeta(x_{1},\,x_{2}).$ Рассмотрим распределение вероятностей $\pi,$ отличное от нуля только на исходах $x_{1},\, x_{2},$ т.е. $\pi(x_{1})=\pi_{1}\neq 0,\; \pi(x_{2})= \pi_{2} \neq 0, \; \pi_{i}=0$ для $i>2, \pi_{1}+\pi_{2}=1.$ Согласно определению B-энтропии (1) имеем:

$\begin{displaymath}B_{\rho}(\pi)=-\pi_{1}\log[\pi_{1}+\pi_{2}-\pi_{2}\rho(x_{1},... ...2})]- \pi_{2}\log[\pi_{1}-\pi_{1}\rho(x_{2},\,x_{1})+\pi_{2}]=\end{displaymath}$

$\begin{displaymath}-\pi_{1}\log(1-\pi_{2}\rho_{12})-\pi_{2}\log(1-\pi_{1}\rho_{21}).\end{displaymath}$

$\begin{displaymath}B_{\zeta}(\pi)=-\pi_{1}\log[\pi_{1}+\pi_{2}-\pi_{2}\zeta(x_{1... ...})]- \pi_{2}\log[\pi_{1}-\pi_{1}\zeta(x_{2},\,x_{1})+\pi_{2}]=\end{displaymath}$

$\begin{displaymath}-\pi_{1}\log(1-\pi_{2}\zeta_{12})-\pi_{2}\log(1-\pi_{1}\zeta_{21}).\end{displaymath}$

Рассмотрим разность $B_{\zeta}(\pi)-B_{\rho}(\pi)$ , которая по условию теоремы равна нулю:

$\begin{displaymath}0=\pi_{1}\log \frac{1-\pi_{2}\rho_{12}}{1-\pi_{2}\zeta_{12}}+ \pi_{2}\log \frac{1-\pi_{1}\rho_{21}}{1-\pi_{1}\zeta_{21}}.\end{displaymath}$

Для распределения $\pi$ , где $\pi_{1}=\pi_{2}=0.5,$ имеем:

$\begin{displaymath}\log\frac{1-0.5 \rho_{12}}{1-0.5 \zeta_{12}}+\log\frac{1-0.5 \rho_{21}} {1-0.5 \zeta_{21}}=0.\end{displaymath}$

Поскольку расстояние симметрично, то в силу монотонности логарифма последнее равенство влечет равенство нулю слагаемых. Это в свою очередь возможно, вопреки нашему допущению, только при равенстве $\rho_{12}=\zeta_{12},$ значит $\rho\equiv \zeta,$ что и требовалось.

Следствие. Между всевозможными расстояниями $\rho,$ вводимыми на основном множестве , и всевозможными функционалами $B_{\rho}(p),$ зависящими от всевозможных распределений на , имеет место одно-однозначное соответствие.

Действительно, каждому $\rho$ по формуле (1) соответствует один функционал $B_{\rho}(p),$ а по доказанной теореме 1 двум различным расстояниям $\rho$ и $\zeta$ соответствуют различные функционалы $B_{\rho}(p)\not\equiv B_{\zeta}(p).$

B-энтропия сложного ансамбля

Имеются статистически независимые вероятностные ансамбли $X_{n}$ ,
$n\in\{1,\,2,\,... ,N\}$ с соответствующими расстояниями $\rho_{1},\,\rho_{2}\,... ,\rho_{N}.$ Рассмотрим вероятностный ансамбль

исходами которого являются всевозможные упорядоченные

-ки вида $(x_{i_1}^{1},\,x_{i_2}^{2},\,... ,x_{i_N}^N),$ где первое место занимает некоторый исход ансамбля

второе место занимает некоторый исход ансамбля

и т.д. вплоть до некоторого исхода ансамбля

Каждой

-ке приписывается значение вероятности $p=p^{12...N},$ равное произведению вероятностей составляющих исходов: $p_{i_{1}i_{2}... i_{N}}=p_{i_1}^{1}\,p_{i_2}^{2}\,... ,p_{i_N}^{N}.$ Полученный таким образом сложный вероятностный ансамбль называется произведением независимых ансамблей: $X=X_{1}\cdot X_{2}\cdots X_{N}= X_{1,2,...,N}.$

Теорема 2. Для сложного вероятностного ансамбля $X_{1,2,...,N}$ существует расстояние

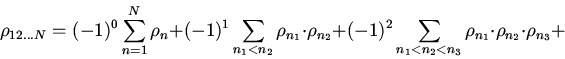
$\begin{displaymath} \rho_{12...N}=(-1)^{0} \sum \limits_{n=1}^{N}\rho_{n}+(-1)^... ..._{n_{1}<n_{2}<n_3} \rho_{n_1}\cdot \rho_{n_2}\cdot \rho_{n_3}+\end{displaymath}$

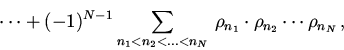$\begin{displaymath} \cdots +(-1)^{N-1}\sum \limits_ {n_{1}<n_{2}<... <n_N}\,\rho_{n_1}\cdot \rho_{n_2}\cdots \rho_{n_N}\,, \end{displaymath}$

(2)

такое, что $B_{\rho_{12...N}}(p^{12...N})=B_{\rho_1}(p^1)+ B_{\rho_2}(p^2)+ ... +B_{\rho_N}(p^N)$ для $\forall p^{n}\,.$

Сначала докажем следующую вспомогательную лемму.

Лемма. Для произведения $X_{1,2}$ двух вероятностных ансамблей и с расстояниями, соответственно, $\alpha,\,\beta$ и распределениями вероятностей $a,\,b$ существует расстояние $\rho$ такое, что $B_{\rho}=B_{\alpha}(a)+B_{\beta}(b),$ и оно выражается формулой

$\begin{displaymath} \rho=\alpha+\beta-\alpha\beta\,. \end{displaymath}$

(3)

Пусть в ансамбле исходов, а в ансамбле исходов. Доказательство леммы начнем с выражения суммы B-энтропий данных ансамблей согласно формуле (1). Имеем

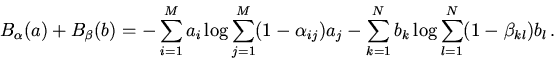
$\begin{displaymath}B_{\alpha}(a)+B_{\beta}(b)=-\sum\limits_{i=1}^{M}a_{i} \log\s... ..._{k=1}^{N}b_{k} \log\sum\limits_ {l=1}^{N}(1-\beta_{kl})b_l\,.\end{displaymath}$

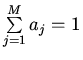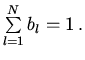
Далее проводим преобразования, используя равенства $\sum \limits_{j=1}^{M}a_{j}=1$ и $\sum \limits_{l=1}^{N}b_{l}=1\,.$

$\begin{displaymath}B_{\alpha}(a)+B_{\beta}(b)=-\sum\limits_{i=1}^{M}a_{i} \log[\... ...limits_{l=1}^{N} b_{j}-\sum\limits_{l=1}^{N} \beta_{kl}b_{l}]=\end{displaymath}$

$\begin{displaymath}-\bigl[\sum\limits_{i=1}^{M}a_{i} \log(1-\sum\limits_{j=1}^{M... ...}^{N}\beta_{kl}b_{l}) \bigr] \cdot \sum\limits_{i=1}^{M}a_{i}=\end{displaymath}$

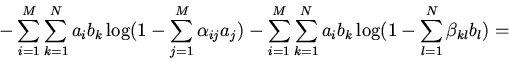
$\begin{displaymath}-\sum \limits_{i=1}^{M} \sum \limits_{k=1}^{N}a_{i}b_{k}\log(... ...its_{k=1}^{N}a_{i}b_{k}\log(1-\sum_{l=1}^{N} \beta_{kl}b_{l})=\end{displaymath}$

$\begin{displaymath}-\sum \limits_{i=1}^{M} \sum \limits_{k=1}^{N}\bigl[a_{i}b_{k... ...j}a_{j})+a_{i}b_{k}\log(1-\sum_{l=1}^{N}\beta_{kl}b_{l})\bigr]=\end{displaymath}$

$\begin{displaymath}-\sum \limits_{i=1}^{M} \sum \limits_{k=1}^{N}a_{i}b_{k}\bigl... ... \alpha_{ij}a_{j})+\log(1-\sum_{l=1}^{N}\beta_{kl}b_{l})\bigr]=\end{displaymath}$

$\begin{displaymath}-\sum \limits_{i=1}^{M} \sum \limits_{k=1}^{N}a_{i}b_{k}\log\... ...}\alpha_{ij}a_{j})\cdot(1-\sum_{l=1}^{N}\beta_{kl}b_{l})\bigr]=\end{displaymath}$

$\begin{displaymath} -\sum \limits_{i=1}^{M} \sum \limits_{k=1}^{N}a_{i}b_{k}\lo... ...{ij}a_{j})\cdot \sum_{l=1}^{N}\beta_{kl}b_{l})\bigr)\bigr]\,. \end{displaymath}$

(4)

Преобразуем выражение, стоящее в (4) под знаком логарифма в круглых скобках:

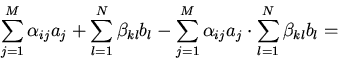
$\begin{displaymath}\sum \limits_{j=1}^{M}\alpha_{ij}a_{j}+\sum \limits_{l=1}^{N}... ...{M}\alpha_{ij}a_{j}\cdot \sum \limits_{l=1}^{N}\beta_{kl}b_{l}=\end{displaymath}$

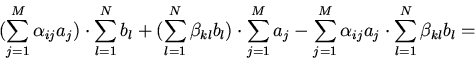
$\begin{displaymath}\bigl(\sum_{j=1}^{M} \alpha_{ij}a_{j}\bigr)\cdot \sum \limit... ...} \alpha_{ij}a_{j}\cdot \sum \limits_{l=1}^{N}\beta_{kl}b_{l}=\end{displaymath}$

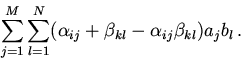
$\begin{displaymath}\sum \limits_{j=1}^{M} \sum \limits_{l=1}^{N}(\alpha_{ij}+\beta_{kl}- \alpha_{ij}\beta_{kl})a_{j}b_{l}\,.\end{displaymath}$

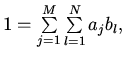Подставим последнее выражение в (4) и, учитывая, что $1=\sum \limits_{j=1}^{M} \sum \limits_{l=1}^{N}a_{j} b_{l},$ получим:

$\begin{displaymath}B_{\alpha}(a)+B_{\beta}(b)=-\sum \limits_{i=1}^{M} \sum \limi... ...(\alpha_{ij}+\beta_{kl}-\alpha_{ij}\beta_{kl})a_{j}b_{l}\bigr]=\end{displaymath}$

$\begin{displaymath}-\sum \limits_{i=1}^{M} \sum \limits_{k=1}^{N} a_{i}b_{k}\lo... ...(\alpha_{ij}+\beta_{kl}-\alpha_{ij}\beta_{kl})a_{j}b_{l}\bigr]=\end{displaymath}$

$\begin{displaymath}-\sum \limits_{i=1}^{M} \sum \limits_{k=1}^{N}a_{i}b_{k} \lo... ...ta_{kl}-\alpha_{ij}\beta_{kl})\bigr] a_{j}b_{l}=B_{\rho}(ab)\,.\end{displaymath}$

Мы пришли к выражению B-энтропии сложного ансамбля $X_{12}=X_{1}\cdot X_{2}$ , соответствующему ее определению (1), если расстояние на основном множестве сложного ансамбля вычислять согласно формуле (3). Лемма доказана.

Доказательство теоремы проведем полной математической индукцией. Для двух ансамблей справедливость формулы (2) вытекает из леммы. Допустим, что формула (2) справедлива для и полученное с ее помощью расстояние $\rho_{12...N}$ используем в качестве отправного пункта индукции. Рассмотрим сложный ансамбль -- результат умножения ансамбля $X_{1,2,...,N}$ на некоторый новый ансамбль $X_{N+1}.$ Для вычисления расстояния на сложном ансамбле $X_{1,2,...,N}\cdot X_{N+1}$ применим формулу, справедливую в случае двух сомножителей:

$\begin{displaymath}\rho_{(12...N),(N+1)}=\rho_{12...N}+\rho_{N+1}-\rho_{12...N}\cdot\rho_{N+1}\,.\end{displaymath}$

В результате сложения первых двух слагаемых получается:

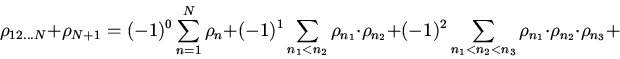
$\begin{displaymath}\rho_{12...N}+\rho_{N+1}=(-1)^{0} \sum \limits_{n=1}^{N}\rho_... ..._{n_{1}<n_{2}<n_3} \rho_{n_1}\cdot \rho_{n_2}\cdot \rho_{n_3}+\end{displaymath}$

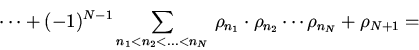
$\begin{displaymath}\cdots +(-1)^{N-1}\sum \limits_{n_{1}<n_{2}<... <n_N}\,\rho_{n_1}\cdot \rho_{n_2}\cdots \rho_{n_N}+\rho_{N+1}=\end{displaymath}$

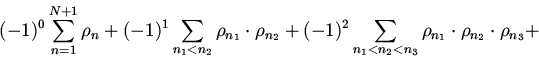
$\begin{displaymath}(-1)^{0} \sum \limits_{n=1}^{N+1}\rho_{n}+(-1)^{1}\sum \limit... ..._{n_{1}<n_{2}<n_3} \rho_{n_1}\cdot \rho_{n_2}\cdot \rho_{n_3}+\end{displaymath}$

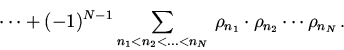
$\begin{displaymath}\cdots +(-1)^{N-1}\sum \limits_{n_{1}<n_{2}<... <n_N}\,\rho_{n_1}\cdot \rho_{n_2}\cdots \rho_{n_N}\,.\end{displaymath}$

Третье слагаемое $\rho_{12...N}\cdot\rho_{N+1}$ равно следующему:

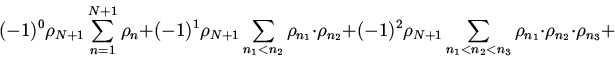
$\begin{displaymath} (-1)^{0}\rho_{N+1}\sum\limits_{n=1}^{N+1}\rho_{n}+(-1)^{1}\... ..._{n_{1}<n_{2}<n_3} \rho_{n_1}\cdot \rho_{n_2}\cdot \rho_{n_3}+\end{displaymath}$

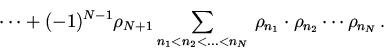
$\begin{displaymath}\cdots +(-1)^{N-1}\rho_{N+1}\sum\limits_{n_{1}<n_{2}<... <n_N}\,\rho_{n_1}\cdot \rho_{n_2}\cdots \rho_{n_N}\,.\end{displaymath}$

Вычитая это выражение из суммы первых двух слагаемых, будем комбинировать "положительные"

-индексные суммы с "отрицательными"

-индексными:

$\begin{displaymath}\rho_{(12...N),(N+1)}= \sum\limits_{n=1}^{N+1}\rho_{n}+\bigl[... ..._{n_2}-(-1)^{0}\rho_{N+1}\sum\limits_{n=1} {N}\rho_{n} \bigr]+\end{displaymath}$

$\begin{displaymath}+\bigl[(-1)^{2}\sum \limits_{n_{1}<n_{2}<n_3}\rho_{n_1}\cdot ... ...limits_{n_{1}<n_{2}}\rho_{n_1} \cdot \rho_{n_2}\bigr]+\cdots +\end{displaymath}$

$\begin{displaymath}\bigl[(-1)^{N-1}\sum \limits_ {n_{1}<n_{2}<... <n_N}\,\rho_{... ...{N-1}}\,\rho_{n_1}\cdot \rho_{n_2}\cdots \rho_{n_{N-1}}\bigr]+\end{displaymath}$

$\begin{displaymath} +\rho_{n_1}\cdot \rho_{n_2}\cdots \rho_{n_N}\cdot \rho_{n_{N+1}}\,. \end{displaymath}$

(5)

Далее символами биномиальных коэффициентов $C_{N}^{M}$ мы будем указывать над знаком суммы число ее слагаемых. При $M\leq N$ из начального отрезка ряда натуральных чисел $1,\,2\,... ,N$ можно выбрать именно $C_{N}^{M}$ различных упорядоченных по возрастанию подпоследовательностей длины

В силу этого содержимое типичной квадратной скобки в (5) можно записать следующим образом.

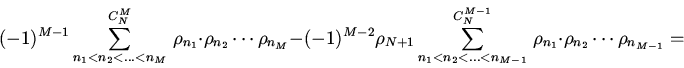
$\begin{displaymath}(-1)^{M-1}\sum \limits^{C_{N}^{M}} _{n_{1}<n_{2}<... <n_M}\,... ..... <n_{M-1}}\,\rho_{n_1}\cdot \rho_{n_2}\cdots \rho_{n_{M-1}}=\end{displaymath}$

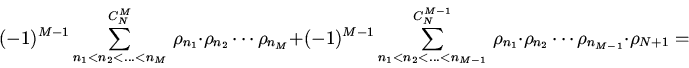
$\begin{displaymath}(-1)^{M-1}\sum \limits^{C_{N}^{M}} _{n_{1}<n_{2}<... <n_M}\,... ...rho_{n_1}\cdot \rho_{n_2}\cdots \rho_{n_{M-1}}\cdot\rho_{N+1}=\end{displaymath}$

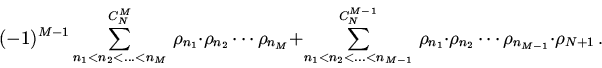
$\begin{displaymath}(-1)^{M-1}\sum \limits^{C_{N}^{M}} _{n_{1}<n_{2}<... <n_M}\,... ...o_{n_1}\cdot \rho_{n_2}\cdots \rho_{n_{M-1}}\cdot\rho_{N+1}\,.\end{displaymath}$

Воспользовавшись комбинаторным равенством $C_{N}^{M}+C_{N}^{M-1}= C_{N+1}^{M}\,,$ заключаем, что здесь имеет место сумма всех $C_{N+1}^{M}$ различных произведений с

сомножителями $\rho_{n_k}$ каждое, где индексы упорядочены по возрастанию и принимают значения от

до

Такую сумму в соответствии с принятыми обозначениями можем записать как

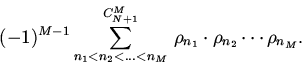
$\begin{displaymath}(-1)^{M-1}\sum \limits^{C_{N+1}^{M}} _{n_{1}<n_{2}<... <n_M}\,\rho_{n_1}\cdot \rho_{n_2}\cdots \rho_{n_M}.\end{displaymath}$

Заменяя подобными символами соответствующие комбинации в (5), получим следующее выражение для расстояния сложного ансамбля:

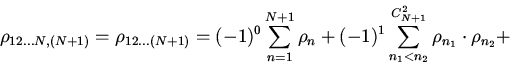
$\begin{displaymath} \rho_{12...N,(N+1)}=\rho_{12...(N+1)}= (-1)^{0} \sum \limi... ...\limits^{C_{N+1}^{2}} _{n_{1}<n_2} \rho_{n_1}\cdot \rho_{n_2}+\end{displaymath}$

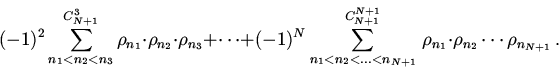
$\begin{displaymath}(-1)^{2}\sum \limits^{C_{N+1}^{3}} _{n_{1}<n_{2}<n_3}\rho_{n... ...<n_{N+1}}\, \rho_{n_1}\cdot \rho_{n_2}\cdots \rho_{n_{N+1}}\,.\end{displaymath}$

Таким образом, мы пришли к выражению типа (2), но для числа сомножителей в сложном ансамбле на единицу большего. Это и доказывает теорему 2 о представлении расстояния сложного ансамбля через расстояния простых ансамблей.

Некоторые свойства и примеры

Для сложного ансамбля $Z=X\cdot Y$ расстояние $\rho,$ выражаемое формулой (3), тоже является "рандомизированным", т.к. его можно рассматривать как билинейнуюй функцию от $\alpha$ и $\beta,$ которая на единичном квадрате принимает неотрицательные значения, не превосходящие единицы. Это свойство транзитивно переносится на сложные ансамбли с любым числом сомножителей.

Расстояние $\rho,$ симметрично, если симметричны $\alpha$ и $\beta.$ Действительно, имеем

$\begin{displaymath}\rho(z_{1},z_{2})=\alpha(x_{1},x_{2})+\beta(y_{1},y_{2})-\alpha(x_{1},x_{2}) \cdot\beta(y_{1},y_{2})=\end{displaymath}$

$\begin{displaymath}\alpha(x_{2},x_{1})+\beta(y_{2},y_{1})-\alpha(x_{2},x_{1})\cdot\beta(y_{2},y_{1})=\end{displaymath}$

$\begin{displaymath}\rho\Bigl((x_{2},y_{2}),(x_{1},y_{1})\Bigr)=\rho(z_{2},z_{1})\,.\end{displaymath}$

Легко проверяется и свойство: $\rho(z_{1},z_{2})=0$ влечет $z_{1}=z_{2},$ если по отдельности $\alpha(x_{1},x_{2})=0$ влечет $x_{1}=x_{2}$ и $\beta(y_{1},y_{2})=0$ влечет $y_{1}=y_{2}$ . Наконец, как показывает проверка с помощью компьютерного моделирования, $\rho$ -- метрика, если $\alpha$ и $\beta$ суть метрики. Однако для строгого обоснования последнего надо еще найти доказательство справедливости неравенства треугольника. Все перечисленные свойства по транзитивности переносятся на любое число ансамблей-сомножителей.

Шенноновская энтропия является частным случаем B-энтропии при специфическом расстоянии, принимающем значения только и : $\rho_{ij}=1$ при $i\not=j, \rho_{ii}=0.$ Геометрической моделью здесь может служить размещение исходов в вершинах -мерного единичного симплекса. -энтропия предоставляет возможность размещать исходы в произвольных точках симплекса, но кроме того существует бесчисленное множество возможностей задания расстояний, отличающихся от такового в евклидовом симплексе.

Из формулы (1) видно, что при любом фиксированном распределении вероятностей -энтропия достигает максимального значения именно на "шенноновском" расстоянии. В самом деле, любое уменьшение значения некоторого $\rho_{ij}$ по отношению к единице увеличивает сумму, стоящую под знаком логарифма, приближая ее к максимальному единичному значению. Тем самым абсолютное значение логарифма уменьшается, т.е. уменьшается и значение -энтропии. При сближении между собой исходов ансамбля -энтропия уменьшается и при нулевых расстояниях между всеми исходами она оказывается равной нулю, что интуитивно согласуется с отсутствием неопределенности выбора.

Рассмотрим простой пример. Имеются четыре сумки одинаковой стоимости -- 100 рублей каждая, но в них содержатся весьма различные денежные суммы, которые ниже мы будем указывать без обозначения единицы измерения: 1) 200, 2) 1000, 3) 5000, 4) 20200. Пусть производится случайный выбор номеров сумок, доставляющий выбирающему сумку с деньгами в собственность. В качестве расстояния между исходами возьмем разность соответствующих стоимостей, отнесенную к максимальной разнице стоимостей -- 20000.

В приводимой таблице данному варианту соответствует первая строка, где мера неопределенности составляет Далее в таблице приведены варианты с постепенно убывающей к нулю неопределенностью.

Стоимость 1	Стоимость 2	Стоимость 3	Стоимость 4	B-энтропия
300	1100	5100	20300	0,8074
300	900	4000	18000	0,6728
300	800	3000	14000	0,4770
300	500	2000	9000	0,2828
300	400	1500	6000	0,1765
300	400	1500	4000	0,1150
300	400	500	1000	0,0200
300	350	400	500	0,0059
300	310	320	330	0,0009

В данном примере все "потребительские" достоинства выбираемых предметов спроецированы на одномерную шкалу стоимостей, хотя очевидно, что далеко не всегда "деньги решают все". Поэтому если в какой-то ситуации более важными оказываются, например, огнеупорность изделия, его герметичность, его вес, удобство открывания - закрывания, то, задавая эти качества в некоторых баллах, мы получаем возможность строить "многомерные" расстояния, и тогда -энтропия послужит более тонким критерием для оценивания неопределенности выбора.

Литература

1: Weiss P. "Subjektive Unsicherheit und Subjective Infomation", Kybernetik, v.5, 2, Западный Берлин, 1968.
2: Колесник В.Д., Полтырев Г.Ш.. Курс теории информации. М.: Наука, ГРФМЛ, 1982, с.24.
3: Леус В.А. "Геометрический подход к численному представлению энтропии." Четвёртый Сибирский конгресс по прикладной и индустриальной математике (ИНПРИМ-2000), посвященный памяти М.А.Лаврентьева (1900-1980), тезисы докладов, часть II, стр.90. Новосибирск, 2000.

Ваши комментарии

[Головная страница]
[Конференции]
[СО РАН]

© 2001, Сибирское отделение Российской академии наук, Новосибирск
© 2001, Объединенный институт информатики СО РАН, Новосибирск
© 2001, Институт вычислительных технологий СО РАН, Новосибирск
© 2001, Институт систем информатики СО РАН, Новосибирск
© 2001, Институт математики СО РАН, Новосибирск
© 2001, Институт цитологии и генетики СО РАН, Новосибирск
© 2001, Институт вычислительной математики и математической геофизики СО РАН, Новосибирск
© 2001, Новосибирский государственный университет
Дата последней модификации Saturday, 08-Sep-2001 19:39:58 NOVST