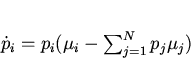Производство информации в ходе микроэволюции проточных гаплоидных популяций.
Вариационный подход на основе формализма Джейнса 1

Евдокимов Е.В., Шаповалов А.В.
Томский государственный университет

Аннотация:

На основе статистического формализма Джейнса предложен вариационный принцип, описывающий динамику микроэволюции проточных гаплоидных популяций. Получены явные соотношения, представляющие динамику отбора в этих системах и производство информации о генетической структуре популяции. Проанализированы биологические аспекты основных элементов вариационного принципа.

A variation principle is proposed to describe micro-evolution dynamics of flow haploid populations in the framework of the Janes statistical formalism. The selection dynamics and information production of the population genetic structure are presented in explicit form for the systems under consideration. Biological meaning of basic elements of the variation principle is considered.

Изучение микроэволюционных процессов в биологических популяциях предполагает описание изменений в их генетической структуре в ходе отбора. По степени перераспределения генных частот судят об интенсивности этих процессов. Однако в большинстве случаев прямое измерение генных частот невозможно по объективным причинам в силу технических сложностей получения информации на уровне нуклеотидных последовательностей в ДНК. При экспериментальных исследованиях как на молекулярном, так и на клеточном уровнях возникает проблема неполноты их описания с помощью моделей Фишера - Эйгена [1]

\begin{displaymath} \dot p_i=p_i(\mu_i-\sum_{j=1}^N p_j\mu_j) \end{displaymath} (1)

из-за практической труднодоступности информации на микроуровне. Здесь $ p_i $ -- доля особей $i$-го генотипа в популяции, $\mu_i$ -- их удельная скорость размножения (мальтузианский параметр), $N$ -- число генотипов в популяции. Для данной системы методами гамильтонова и лагранжева анализа установлено, что ее динамика подчиняется вариационному принципу, имеющему смысл минимизации скорости изменения информации о генетической структуре популяции в ходе отбора [2,3].

Традиционный подход к решению данной проблемы состоит в использовании измеряемых макропараметров популяции, отражающих ход эволюционного процесса, например среднего значения признака, по которому идет отбор. М. Эйгеном было предложено оценивать скорость микроэволюционных процессов по производству информации, связанной с перераспределением генных частот, посредством информационной меры Кульбака [4,6]. В этой связи представляет интерес теоретический анализ микроэволюционных процессов с использованием меры Кульбака и практических методов ее измерения на основе макропараметров. Одним из известных подходов такого рода является формализм Джейнса, основанный на эвристическом "принципе максимального правдоподобия" предсказания поведения системы при недостатке информации о ней. Согласно Джейнсу [6] наименее предубежденный (наименее ошибочный) способ нахождения распределения вероятностей системы тот, который максимизирует (целевую) функцию, выражающую неопределенность системы при условиях имеющейся информации ( "принцип максимальной неопределенности"). В этом подходе формулируется вариационный принцип максимизации шенноновской меры неопределенности, информационной энтропии рассматриваемой системы. Варьирование информационной энтропии, при наличии уравнений связи между вероятностями различных состояний системы и ее измеряемыми макропараметрами типа средней энергии, дает в итоге функцию распределения вероятностей в явном виде [7,8].

Адаптируем "принцип максимального правдоподобия" для описания эволюции популяций. Поскольку речь идет не о равновесном состоянии системы, а о процессе отбора, модифицируем формализм Джейнса следующим образом.

В соответствии с общим подходом потребуем, чтобы процесс эволюции популяций протекал наименее неожиданным способом.

Рассмотрим вначале эволюцию более простых систем -- турбидостатных гаплоидных популяций, соответствующих дарвиновским системам с постоянной организацией и постоянными мальтузианскими параметрами. Множество генотипов особей, составляющих популяцию, обозначим $G$, а множество соответствующих им фенотипов (мальтузианских параметров) через $M$. Положим, что отдельные дискретные генотипы $g_i$ $(g_i \in G,\, i = 1,\ldots ,N)$ однозначно определяют значения фенотипов, мальтузианских параметров $(\mu_i \in M,\,\mu_i = const, i=1,\ldots ,N)$, для носителей данных генотипов (здесь $N$ -- как и ранее, число генотипов в системе). Это требование естественно для популяций с неполовым размножением. При случайном выборе какой-либо особи из исследуемой популяции в момент времени $t$ ее фенотип, мальтузианский параметр, заранее не известен. Определим его как случайную величину $\mu$, принимающую дискретные значения $\mu_i$ из множества $M$. Вероятность того, что случайно выбранная в момент $t$ особь имеет мальтузианский параметр $\mu_i$, определим как

\begin{displaymath} P_i(t)=P_\mu(\mu=\mu_i,t),\quad \sum_{i=1}^N P_i=1,\quad i=1,\ldots,N. \end{displaymath} (2)

Эта величина -- статистический аналог популяционной переменной $ p_i $ в (1). $P_\zeta(t) (\zeta=1,\ldots,N)$ как функция всех возможных значений $\mu_\zeta$ случайной величины $\mu$ есть функция распределения вероятностей этой величины. Она описывает состояние популяции, ее генетическую структуру в различные моменты времени. Среднепопуляционное значение мальтузианского параметра $<\mu >$ определяется через функцию $P_\zeta(t)$ следующим образом:
\begin{displaymath} <\mu>=<\mu>(t)=\sum_{i=1}^N P_i(t)\mu_i. \end{displaymath} (3)

Важным является то, что величина $<\mu >$ доступна прямым экспериментальным измерениям. В начальный момент времени величины $P_{i0}=P_i(t)\vert _{t=0}$ также доступны прямому измерению, так как задаются экспериментально.

Поставим задачу -- найти вид функции $P_\zeta(t)$, используя информацию о $<\mu >$ и $P_{\zeta 0}$, исходя из вариационного подхода, подобного формализму Джейнса.

Определим вид варьируемой функции. В ходе эволюции турбидостатной популяции в результате отбора происходит изменение частот генотипов и соответствующей им функции распределения, $P_{\zeta 0}\Rightarrow P_\zeta(t)$. Поэтому вместо применяемого Джейнсом для описания равновесных состояний информационной меры Шеннона в данном подходе необходимо использовать другую информационную меру, отражающую ожидаемую неопределенность результатов отбора, или, по терминологии Реньи [9], неожиданность протекания процесса эволюции. В качестве меры неожиданности $i$-го события в теории информации [10] используется величина $\log(1/p_i)$, где $ p_i $ - вероятность этого события. Соответственно, изменение неожиданности для $i$-го генотипа в ходе отбора можно определить как $[\log(1/P_{i0})-\log(1/P_i(t))]$. Усредняя по всей популяции в момент времени $t$, получим функцию неожиданности эволюции популяции в виде:

\begin{displaymath} I(P_i(t)/P_{i0})=\sum_{i=1}^N P_i(t)\log(P_i(t)/P_{i0}). \end{displaymath} (4)

Эта функция совпадает с указанной выше оценкой производства информации в ходе отбора [4], она также известна как мера информационного расстояния между двумя распределениями, мера Кульбака [5].

Таким образом, декларируемый в данной работе принцип минимальной неожиданности протекания эволюции идентичен принципу минимального производства информации в ходе отбора или минимальной скорости прохождения системы по координате информационного расстояния. Здесь под информацией понимается информация о функции распределения генотипов в популяции.

Сформулируем соответствующий вариационный принцип следующим образом:

\begin{displaymath} \begin{array}{l} I(P_i(t)/P_{i0})\Rightarrow \min,\\ \delta [I(P_i(t)/P_{i0})]=0 \end{array} \end{displaymath} (5)

при выполнении условий (2) и (3), когда $<\mu >$ считается заданной (измеренной) величиной.

Функцию $P_\zeta(t)$ в соответствии с подходом Джейнса найдем методом неопределенных множителей Лагранжа. Обозначим множители Лагранжа через $\lambda_0$ и $\lambda_1$ и введем функцию Лагранжа

\begin{displaymath} \tilde I=\sum_{i=1}^N P_i\log\displaystyle\frac{P_i(t)}{... ...=1}^N (P_i(t)-1)-\lambda_1 (\sum_{i=1}^N P_i(t)\mu_i-<\mu>). \end{displaymath} (6)

Условие экстремума функции (6) $(\partial\tilde I/\partial P_i=0 )$ дает
\begin{displaymath} P_i(t)=P_{i0}\exp(\mu_i\lambda_1)/\exp(\lambda_0). \end{displaymath} (7)

Подстановка (7) в (2) приводит к выражению для первого множителя Лагранжа
\begin{displaymath} \lambda_0=\log\sum_{k=1}^N P_{k0}\exp(\mu_k\lambda_1). \end{displaymath} (8)

Соответственно, наименее неожиданные значения $P_i(t)$, получаем, подставляя (8) в (7),
\begin{displaymath} P_i(t)=\displaystyle\frac{P_{i0}\exp(\mu_i\lambda_1)}{\sum_{k=1}^N P_{k0}\exp(\mu_k\lambda_1)}. \end{displaymath} (9)

Заметим, что полученное выражение определяет минимум функции неожиданности, так как второй дифференциал варьируемой функции есть положительно определенная квадратичная форма. Вид функции распределения $P_\zeta(t)$ получим, выяснив биологический смысл второго множителя Лагранжа $\lambda_1$. Для этого рассмотрим, как меняется в ходе отбора соотношение частот (вероятностей) двух любых генотипов в системе, например $i$-го и $k$-го, при равных начальных значениях. Из (9) непосредственно получим
\begin{displaymath} \log(P_i(t)/P_k(t))=(\mu_i-\mu_k)\lambda_1. \end{displaymath} (10)

Из этого выражения, во-первых, можно определить размерность $\lambda_1$. Так как размерность мальтузианских параметров -- это размерность скорости реакции первого порядка, (ч$^{-1}$ или с$^{-1}$), то, соответственно, $\lambda_1$ имеет размерность времени. Во-вторых, видно, что с ростом $\lambda_1$ реализуется кинетическое преимущество одного генотипа над другим в соответствии с величиной и знаком $(\mu_i-\mu_k)$ как и с увеличением времени эволюции системы. Это позволяет идентифицировать второй неопределенный множитель Лагранжа $\lambda_1$ как момент времени $t$. В результате выражение (9) принимает вид
\begin{displaymath} P_i(t)=P_{i0}e^{\mu_i t}\bigg /\sum_{k=1}^N P_{k0}e^{\mu_k t}. \end{displaymath} (11)

Соответственно, для первого множителя Лагранжа имеем
\begin{displaymath} \lambda_0=\log\sum_{i=1}^N P_{i0}e^{\mu_i t}. \end{displaymath} (12)

Необходимо отметить, что выражение (11) с точностью до соответствия между $ p_i $ и $P_i(t)$ идентично решению системы уравнений Фишера-Эйгена (1).

Рассмотрим биологический смысл $\lambda_0$. Величина $\lambda_0$ безразмерна. Дифференцируя (12) по времени, получим

\begin{displaymath} \displaystyle\frac{d\lambda_0}{dt}=\sum_{i=1}^N \mu_i\lef... ... P_{k0}e^{\mu_k t}} \right )=\sum_{i=1}^N\mu_i P_i(t)=<\mu>, \end{displaymath} (13)

т.е. среднепопуляционное значение мальтузианского параметра. Вторая производная $\lambda_0$ по времени определяет дисперсию мальтузианского параметра в популяции:
\begin{displaymath} \displaystyle\frac{d^2\lambda_0}{dt^2}=\sum_{i=1}^N P_i(t... ...- (\sum_{i=1}^N P_i(t)\mu_i)^2=<\mu^2>-<\mu>^2=\sigma_\mu^2. \end{displaymath} (14)

Оба эти показателя являются важными среднестатистическими характеристиками популяции, их измерение по экспериментальным данным или полевым наблюдениям -- необходимый элемент всех экологических исследований. Дальнейшее дифференцирование по времени дает центральные моменты высших порядков.

Следствием выражений (13) и (14) является известная "основная теорема естественного отбора" Фишера , связывающая дисперсию мальтузианского параметра в популяции и интенсивность отбора, измеряемую через скорость изменения его среднепопуляционного значения:

\begin{displaymath} \displaystyle\frac{d<\mu>}{dt}=\sigma_\mu^2. \end{displaymath} (15)

Обращает на себя внимание сходство выражения для $\lambda_0$ (12) и "статистической суммы" в статистической физике и известной также как "большой термодинамический потенциал" [7].

Полезным для экспериментальной практики является следствие из (13) вида

\begin{displaymath} \lambda_0=\int_0^t<\mu>d\tau, \end{displaymath} (16)

так как этот интеграл можно измерить инструментально. В частности, в турбидостате, в котором $<\mu >$ равна протоку через систему [11], этот интеграл равен отношению суммарного объема культуры, собранной за время наблюдения $t$ (или суммарному количеству питательной среды, поданной в ферментер), к объему ферментера. Другим, более приближенным, способом является численное интегрирование экcпериментально измеренной кривой $<\mu> (t)$.

На основе полученных соотношений можно решить поставленную вначале работы задачу -- количественно оценить производство информации в ходе эволюции турбидостатной популяции. Из выражений (4) и (11) получаем

  $\textstyle I(P_i(t)/P_{i0})=\sum_{i=1}^N P_i(t)\log(P_i(t)/P_{i0})=$    
  $\textstyle \mbox=\sum+{i=1}^N P_i(t)\log(e^{\mu_i t}/\sum_{k=1}^N P_{k0}e^{\mu_k t})=$    
  $\textstyle \mbox{}=\sum_{i=1}^N P_i(t)\mu_i t-\sum_{i=1}^N P_i(t)\log(\sum_{k=1}^N P_{k0}e^{\mu_k t})=<\mu>t-\lambda_0.$   (17)

Как указывалось выше, все входящие в это выражение члены допускают экспериментальное определение по измеряемым макропараметрам.

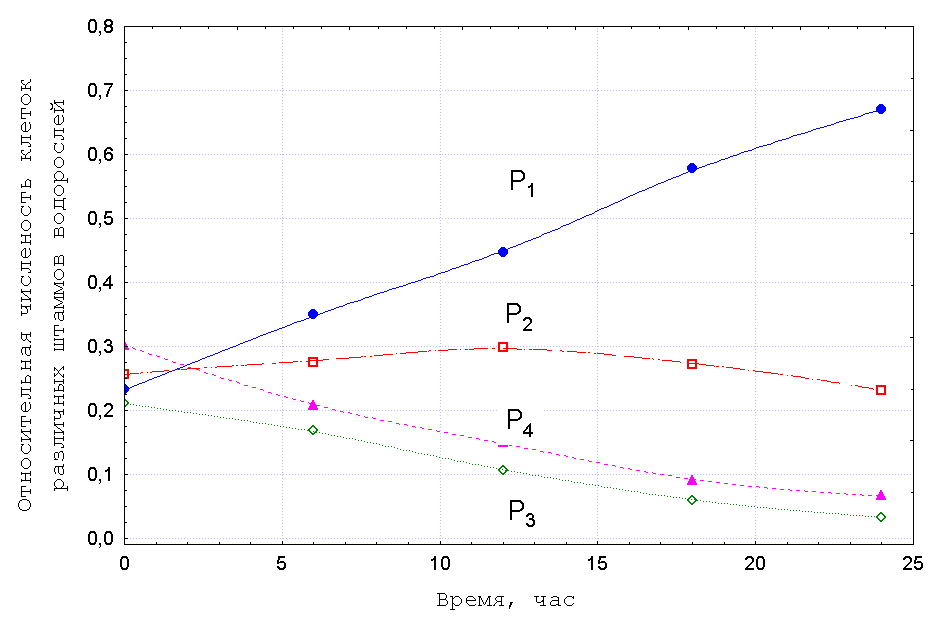
Проиллюстрируем этот подход экспериментом, выполненным Л. Н. Цоглиным с сотрудниками, в котором изучали ход отбора разных штаммов микроводорослей при проточном культивировании в турбидостате [12]. На Рис.1 представлены изменения относительных концентраций клеток разных штаммов, $ P_i$, прямо измеренные в ходе опыта с помощью камеры Горяева под микроскопом.

Рис. 1: Изменение относительных концентраций клеток микроводорослей различных штаммов в ходе отбора при культивировании в турбидостате (цит. по Л.Н.Цоглину и др. [12]). $ P_i$ - обозначения различных штаммов.

Рис. 2: Изменение средней удельной скорости роста популяции микроводорослей в ходе микроэволюции.

Рис. 3: Производство информации $I(P_i(t)/P_{i0})$ в ходе микроэволюции популяции микроводорослей, определенное по данным об относительной численности клеток разных штаммов (Рис. 1), и на основе изменения макропараметра $<\mu >$ (Рис.2) при использовании выражения (17).

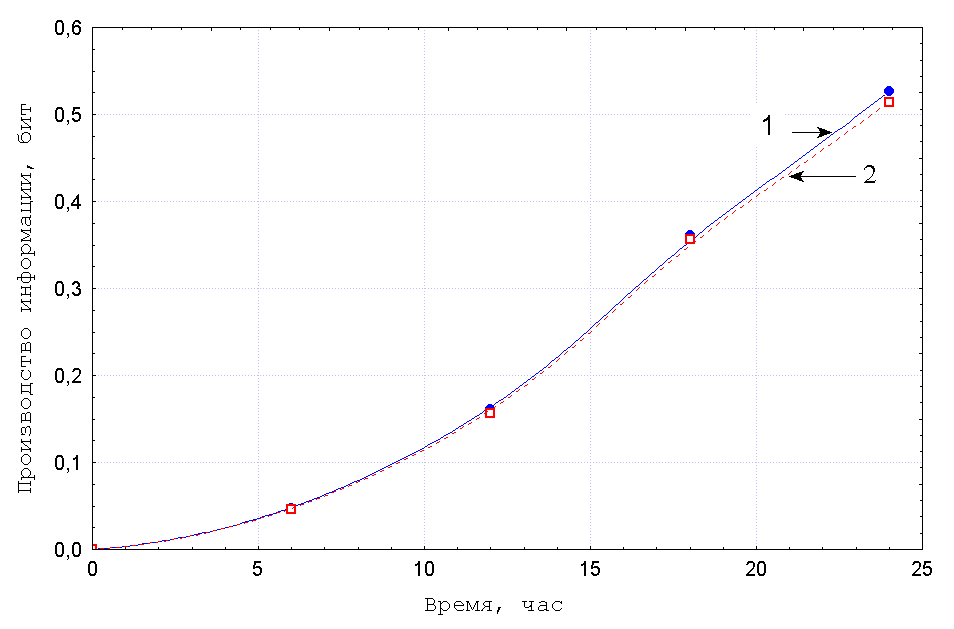Как видно из рисунка, указанные кривые совпадают с точностью до ошибки измерений, что свидетельствует об адекватности предлагаемого нами подхода.

Эволюционная динамика популяций в хемостате является более сложной, т.к. удельные скорости размножения $\mu_i (=\mu_i(S) )$ являются функциями времени вследствие нестационарности концентрации лимитирующего субстрата $S$. В данном случае в качестве измеряемой (заданной) величины выберем среднюю по популяции и по времени удельную скорость роста

\begin{displaymath} <\tilde\mu>=\sum_{i=1}^N P_i\cdot\displaystyle\frac 1t\int_0^t\mu_i(\tau)d\tau. \end{displaymath} (18)

Применение вариационного принципа (5), в котором условие (3) заменено условием (18), дает

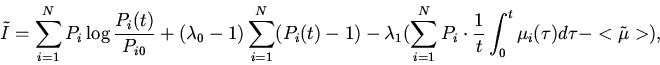
\begin{displaymath} \tilde I=\sum_{i=1}^N P_i\log\displaystyle\frac{P_i(t)}{P_{... ... \displaystyle\frac 1t\int_0^t\mu_i(\tau)d\tau-<\tilde\mu>), \end{displaymath}


\begin{displaymath} \displaystyle\frac{\partial \tilde I}{\partial P_i} = \l... ...mbda_1 \displaystyle\frac{1}{t}\int_0^t \mu_i(\tau) d\tau=0. \end{displaymath} (19)

Полагая $\lambda_1 = t $, по аналогии с рассмотренным выше случаем турбидостата, получим
\begin{displaymath} P_i(t)=P_{i0}\exp(\int_0^t\mu_i(\tau)d\tau)\bigg/\sum_{k=1}^NP_{k0} \exp(\int_0^t\mu_k(\tau)d\tau), \end{displaymath} (20)


\begin{displaymath} \lambda_0=\log\sum_{k=1}^N P_{k0}\exp(\int_0^t\mu_i(\tau)d\tau). \end{displaymath} (21)

Соотношения (20) и (21) естественным образом обобщают формулы (11) и (12) для турбидостата. Если выражение (20) дополнить "уравнениями состояния", связывающими $\mu_i$, $S$ и $ P_i$ , то (20) будет представлять собой известную интегральную форму уравнений многомерного хемостата. Множитель Лагранжа $\lambda_0$ имеет тот же биологический смысл, что и в случае турбидостата.

Из (20) и (21) непосредственно получается явное выражение для производства информации в ходе эволюции хемостатной популяции

\begin{displaymath} I(P_i(t)/P_{i0})=<\tilde\mu>t-\lambda_0=\sum_{i=1}^N P_i\cdot\int_0^t \mu_i(\tau)d\tau-\int_0^t<\mu>d\tau. \end{displaymath} (22)

Как известно (см., например, [13]), регулярный режим работы хемостата (после завершения начальных переходных процессов) характеризуется линейной зависимостью $\mu_i$ от $S$. В этих условиях производство информации (22) при использовании известных уравнений хемостата [13] представимо в виде
\begin{displaymath} I(P_i(t)/P_{i0})=\displaystyle\frac{(\dot X/X)+D}{S}\int_0^tS(\tau)d\tau-\log\displaystyle\frac{X}{X_0}-D\cdot t, \end{displaymath} (23)

где текущая и начальная концентрации биомассы $X$ и $X_0$, удельная скорость роста биомассы $\dot X/X$, концентарция лимитирующего субстрата $S$ и проток $D$ являются макропараметрами системы и могут быть легко измерены экспериментально.


Примечание

... Джейнса.1
Работа поддержана грантами Минобразавания РФ Е00-12.0-239 и Е00-1.0-126

Литература

1
Эйген М., Шустер П. Гиперцикл. Принципы самоорганизации макромолекул. Мир, M., 1982.

2
Евдокимов Е.В., Шаповалов А.В.//Изв. вузов. Физика. 7, 1997, 23-28.

3
Shapovalov A.V., Evdokimov E.V. //Physica D. 112, 3-4, 1998, 441-450.

4
Эйген М., Винклер Р. Игра Жизни. Наука, M., 1979.

5
Kullback S., Leiber R. // Ann. of Math.Stat. 22, 1951, 79-87.

6
Janes E.T. //Phys.Rev. 108, 1957, 171-184.

7
Трайбус М. Термостатика и термодинамика. Энергия, M., 1970.

8
Хакен Г. Синергетика. Мир, M., 1980.

9
Renyi A. //Proc.Fourth Berkley Sympos. Statistics and Probability. 1, 1960, 547-561.

10
Шеннон К. Работы по теории информации и кибернетике. ИЛ, M., 1963.

11
Перт С. Дж. Основы культивирования микроорганизмов и клеток. Мир, M., 1978.

12
Цоглин Л.Н., Владимирова М.Г., Семененко В.Е. //Физиология растений. 17, 1970, 1129-1139.

13
Smith H.L., Waltman P. The theory of chemostat: dynamics of microbial competition. Cambridge University Press, London, 1995.
Ваши комментарии
[SBRAS]
[Головная страница]
[Конференции]
[СО РАН]

© 2001, Сибирское отделение Российской академии наук, Новосибирск
© 2001, Объединенный институт информатики СО РАН, Новосибирск
© 2001, Институт вычислительных технологий СО РАН, Новосибирск
© 2001, Институт систем информатики СО РАН, Новосибирск
© 2001, Институт математики СО РАН, Новосибирск
© 2001, Институт цитологии и генетики СО РАН, Новосибирск
© 2001, Институт вычислительной математики и математической геофизики СО РАН, Новосибирск
© 2001, Новосибирский государственный университет
Дата последней модификации Sunday, 07-Oct-2001 14:05:34 NOVST