Распознавание растений по разнотипным признакам на пересекающихся классах-таксонах (на основе теории нечетких множеств)

Красинский В.И.
Центральный сибирский ботанический сад СО РАН, Новосибирск

После первообразной работы Л.Заде [1] по нечетким множествам (НМ) С.Ватанабэ предложил и обосновал [2] обобщение классической функции истинности предикатов на непрерывный интервал [0,1]. Этот подход оказался плодотворным для моделирования тех задач и ситуаций, в которых отсутствуют приборные показания, также для формализации знаний. Преобразование нечетких значений признаков объектов в значения функции принадлежности (ФП) объектов к НМ соответствует измерению этих признаков в единой абстрактной интервальной шкале, что открывает возможности для нестатистического многомерного анализа и классификации. Семантика и алгоритмы этих преобразований составляют предмет прикладных исследований.

Значительной трудностью в задачах диагностики в биологии, в частности, ботанике, является многозначность классов-таксонов по всем признакам. Иначе говоря, значениями числовых и номинальных признаков классов являются списки переменной длины. В такой ситуации невозможно четкое разбиение универсума на подмножества по значениям признаков - нет полной группы несовместных событий по значениям признаков. Многозначность образов-классов соответствует их пересечениям. Поэтому чаще всего неприменимы методы теории вероятностей и математической статистики для моделирования процессов распознавания реальных биологических объектов.

Целью работы являлось создание алгоритма и соответствующей программы @RECOFAM (Recognizer of Families) для диагностики двудольных растений Сибири на уровне семейств. Исходные данные предоставлены д.б.н. И.М.Красноборовым. Классы-семейства растений (всего 102) представлены значениями 11 морфологических признаков: четырех числовых - чисел пестиков, столбиков, тычинок, листочков околоцветника, и семи номинальных - типов околоцветника, соцветия, плода, размножения, завязи, гинецея, листьев.

По всем признакам классы многозначны (нечеткие в признаковом пространстве). Например, по признаку ``тип соцветия'' семейство растений Fabaceae характеризуется списком трех значений: головка, кисть, цветки одиночные. По этому же признаку ``тип соцветия'' семейство Primulaceae имеет список из пяти значений: зонтик, кисть, метелка, цветки одиночные, цветки пазушные. Видно, что эти таксоны частично пересекаются (похожи) по признаку типа соцветия. Пример многозначности по числовому признаку: у растений семейства Saxifragaceae число лепестков бывает 1, 4, 5. Отсюда видна недостаточность интервального способа учета неопределенности для реальных биологических объектов - представители последнего таксона не могут иметь число лепестков 2, 3.

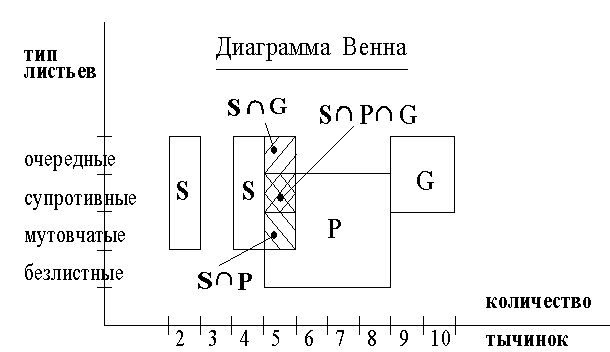
Дополнительные примеры многозначности трех классов-семейств по двум разнотипным признакам приведены в табл. 1. Ниже, на рис. 1, показана соответствующая диаграмма Венна, иллюстрирующая пересечения и разрывы классов-семейств в признаковом пространстве.

Таблица 1:
Классы Тип листьев Число тычинок
Geraniaceae очередные, супротивные 5, 9, 10
Primulaceae безлистные, мутовчатые, супротивные 5, 6, 7, 8
Scrophulariaceae мутовчатые, очередные, супротивные 2, 4, 5

Рис. 1: Пересечения и разрывы классов в признаковом пространстве

Пересечение классов можно трактовать как зашумленность данных, или информационную избыточность. Для оценки средней степени информационной избыточности описания пересекающихся классов-таксонов предлагается коэффициент эксцесса:

\begin{displaymath}ex = \sum x_{mni} / (M \cdot N).\end{displaymath}

Здесь $i$ - индекс значения признака многозначного таксона; $m, n$ - индексы признака и класса; $M$ - число признаков (в нашей задаче 11); $N$ - число классов-семейсв (всего 102); $x_{mni}$ - значение признака класса-таксона в двоичной матрице инцидентности объект-свойство.

Коэффициент $ex$ равен единице в стандартном случае не пересекающихся по значениям признаков классов объектов, то есть в случае полной группы несовместных событий. Он позволяет приближенно оценить среднюю степень неопределенности описания классов как по каждому признаку в отдельности, так и в целом, по всем признакам. Будучи вычисленным по всей исходной двоичной таблице экспериментальных данных (ТЭД 102$\times $94), этот коэффициент получил значение $ex=1.62$, которое в точности равно пропорции золотого сечения, одного из фундаментальных законов природы и искусства.

Соответствие строения и количества разных органов растений числам Фибоначчи известно ботаникам еще со средних веков. Поскольку исходная ТЭД является обобщающей по большинству растений Сибири, факт $ex=1.62$ можно считать не случайным, а свидетельствующим об удачном выборе ботаниками системы признаков для описания семейств растений. Анализ этого факта выходит за рамки проведенного исследования, требуется глубокая биологическая интерпретация. Возможно, в ``золотой'' степени информационной избыточности ТЭД отражается универсальное антиэнтропийное свойство живых систем для сохранения своей устойчивости во внешнем мире.

Применение классических статистических методов, основанных на аксиоматической теории вероятностей, (программные пакеты СИГАМД, STATISTICA) для диагностики растений не привело к успеху именно из-за пересечения классов-таксонов. Поэтому использование теории нечетких множеств и теории возможностей для моделирования многозначности в описаниях классов было вполне обоснованным. Семантика всех НМ-признаков определена как ``ненадежность диагностики'', а именно, чем более многозначен таксон-семейство, тем хуже распознаются его представители по данному признаку. Такая семантика нечеткости таксонов подтверждена ботаниками и поэтому служит цели создания оптимизирующего диалогового алгоритма распознавания (диагностики) растений. Вычисление степени нечеткости многозначных таксонов по каждому признаку снижает размерность признакового пространства, и является преобразованием в сильную интервальную шкалу списковых признаков классов-таксонов, то есть классы становятся ранжированными по каждому признаку (количественному и качественному), причем по единой мере, что создает условия для многомерного анализа.

Цель алгоритма последовательной интерактивной диагностики состоит в минимизации количества вопросов о значениях признаков диагностируемой особи, на основе интегрального критерия, получаемого суперпозицией всех НМ. Этот критерий вычисляется на всех оставшихся кандидатах-таксонах. Применяются три метода суперпозиции НМ: по минимальной нечеткости, по средней нечеткости, по минимуму коэффициента нечеткости Кофмана. Возможен ответ пользователя ``не знаю'' на вопрос о значении любого признака, при этом не возникает тупиковой ситуации, а лишь удлиняется диалог. Реализованный алгоритм соответствует распознающему алгоритму в смысле работы [3], при этом вычисление ФП объектов-классов к НМ по значениям признаков позволило получить числовой интегральный критерий качества диагноза особи, избегая неопределенностей, отмеченных в [3].

Для вычисления ФП многозначных объектов к НМ (степени нечеткости) по числовым признакам разработан новый способ [4], основанный на понятии фокальных элементов (ФЭ, или вложенных подмножествах универсума). Вместо распределения вероятностей значений признака вычисляются распределения мер возможности и необходимости этих значений по двум последовательностям ФЭ исходного множества объектов, в соответствии с теорией Демпстера-Шефера [5], в которой требование полноты группы несовместных событий заменяется распределением единичной ``массы уверенности'' на все возможные события (значения признака). А именно, исходное множество X нечетких объектов разбивается на непустые, попарно различные четкие подмножества

\begin{displaymath}A_1, A_2, ... , A_i.\end{displaymath}

Показано в [6], что если при помощи формулировок i событий построить подмножества $A_i$ как вложенные:
\begin{displaymath} A_1 \subseteq A_2 \subseteq ... \subseteq A_i, \end{displaymath} (1)

то мощности этих подмножеств определят частотные вероятности приращений меры необходимости универсума по событиям $i$:
\begin{displaymath} m(A_i) = (\text{Card} A_i - \text{Card} A_{i-1}) / \text{Card} X \end{displaymath} (2)

Имеется в виду, что $\text{Card}~\emptyset = 0$. Подмножества $A_1, ... , A_i$ как раз называются фокальными элементами. Необходимое условие единичной ``массы уверенности'' $\sum m(A_i) = 1$ будет выполнено, так как результатом эксперимента (измерения) является счетное универсальное множество $X$, и каждый объект $x \in X$ окажется отнесенным только к минимальному по вложению ФЭ.

В совокупности выражений (1) и (2) состоит принцип получения приращения необходимости события i (аналогично вычислению эмпирической функции распределения вероятностей событий). Вычисление ФП объектов к НМ по распределению меры необходимости универсума обосновано в работе [7]:

\begin{displaymath} \forall x, \mu_A(x) = \sum m(A_i) \cdot T_i(x), \end{displaymath} (3)

где $T_i(x)$ - значение характеристической функции принадлежности элемента к четкому подмножеству $A_i$ (функция Хевисайда).

Поскольку признак числовой, то можно построить две последовательности ФЭ в соответствии с группами противоположных событий ``быть меньше или равно $К_i$'' и ``быть больше $К_i$'', где $К_i$ - значение признака в $i$-интервале группировки. Соответственно вычисляются по (3) ФП к двум НМ - слева $L$ и справа $R$. Это позволяет максимально учесть многозначность числовых объектов-классов. Свертка НМ $L$, $R$ в единое НМ $V$ производится по принципу расширения Заде:

\begin{displaymath}\mu_V(x) = \mu_{L \cup R}(x) = \max\{\mu _{ L}(x), \mu _{R}(x)\}, x \in X. \end{displaymath}

Значение $\mu _{{\rm V}~}(x)$ есть степень многозначности класса ``х'' по данному числовому признаку. Семантика дополнительного множества $F = \neg V$ соответствует степени надежности диагноза особи по данному количественному признаку:
\begin{displaymath} \mu _F(x) = 1 - \mu _V(x). \end{displaymath} (4)

Для всех числовых признаков по всем оставшимся объектам-классам производятся преобразования (1)-(4).

Отметим, что предложенный способ формализации нечеткости полностью применим к объектам, описанным ранговыми признаками, так как по ним точно так же можно построить две фокальные последовательнности объектов.

Вычисление ФП таксонов к НМ для номинальных признаков производится на основе теории возможностей с учетом весовых коэффициентов, или ``масс уверенности'' в значениях признаков у многозначных таксонов [8], [9].

Общий алгоритм диагностики неизвестного растения [9], работающий с нечеткими множествами ``надежность диагноза $\mu _F(x)$'', состоит из трех основных циклически выполняемых блоков:

1. Для каждого из оставшихся семейств-кандидатов на диагноз (сначала это все 102 семейства) вычисляются значения функций принадлежности ко всем 11 НМ-признакам.

2. Выбор очередного вопроса по результату суперпозиции (свертки) всех НМ - ранжирование признаков по итоговому критерию априорной надежности диагноза оставшихся объектов. Реализованы три принципа свертки НМ. ``По умолчанию'' установлена осторожная стратегия, но пользователь может изменять выбор.

2.1. Осторожная стратегия, или усредненный выбор, состоит в том, что вычисляется среднее значение ФП для каждого из 11 признаков на всех оставшихся объектах. Признаки ранжируются по убыванию этой ``средней надежности диагноза''. Пользователь, однако, может выбрать любой признак из списка, не обязательно следуя рекомендации программы.

2.2. Рискованная стратегия, или экстремальный выбор, состоит в том, что признаки ранжируются по убыванию максимальных значений своих ФП. Выбрать можно также любой признак. Эта стратегия в небольшом числе случаев дает быструю диагностику (за 1 - 2 ответа на вопросы программы).

2.3. Одним из показателей для оценки степени нечеткости НМ является коэффициент Кофмана $v(F_m)$ - чем он меньше, тем лучше соответствующий признак m подходит для диагностики:

\begin{displaymath} v(F) = (2/N) \times \left(\sum \min (\mu_{F(x_i)}, \mu_{\neg F(x_i)})\right). \end{displaymath}

Здесь $N$ - число объектов.

В программе применяется равноценное операции $\min$ ядро $\vert\mu (x_) - (1 - \mu (x_i))\vert$, на основе которого можно получить расстояние Хемминга-Заде между НМ и его отрицанием:

\begin{displaymath} D_m = \sum \vert\mu (x_i) - (1 - \mu (x_i))\vert, i=1,...,N. \end{displaymath}

Оптимальным для очередного шага диагностики считается тот признак, который имеет максимальное значение $D$.

Это соответствует минимуму нечеткости по Кофману, то есть объекты-классы менее всего ``размазаны'' по градациям значений этого признака, по сравнению со всеми другими.

3. По ответу на вопрос о значении признака, выбранного в п.2, и в соответствии с таблицей исходных данных о 102 таксонах, производится ограничение множества семейств-кандидатов на диагноз, затем - переход к п.1, и так до одного кандидата, либо до появления противоречий в ответах пользователя.

Разработанный алгоритм пошаговой диагностики растениий является примером советующей экспертной системы - анализу по совокупности разнотипных признаков неопределенных ситуаций в целях поиска наилучшего прецедента, среди описанных экспертом. Растения однозначно диагностируются в среднем за 2-4 ответа на вопросы программы о значениях признаков, вместо полного вектора из 11 значений. Программа не имеет тупиковых ситуаций, тестирование ведущими ботаниками подтвердило ее надежность. Ниже, в табл. 2, 3, приводятся примеры диагностики растений по программе @RECOFAM.


Таблица 2: Определение особи по ``броским признакам'', не следуя советам оптимизации
Вопрос Ответ Осталось кандидатов (из 102)
1. листья стебель безлистный 12
2. соцветие зонтик 1 - Primulaceae


Таблица 3: Представитель семейства Rosaceae, но на образце отсутствует плод
Вопрос Ответ Осталось кандидатов (из 102)
1. соцветие метелка 26
2. плод не знаю 26
3. андроцей 2 тычинки 5
4. столбики 3 1 - Rosaceae

Видно, что в примере по табл. 3 ответ ``не знаю'' на вопрос о типе плода не сорвал диагностику представителя этого сложного семейства. Подобное ``разумное'' поведение программы является следствием избыточности исходной информации (большого числа признаков) и описанных выше оптимизационных свойств алгоритма диагностики.

Эффективность алгоритма демонстрируется в табл. 4 путем сравнения количества вопросов до однозначной диагностики одних и тех же растений (представителей трех трудных таксонов) по советам программы и вопреки советам программы, также при выборе очередного признака-вопроса по датчику случайных чисел.


Таблица 4: Число вопросов до точного диагноза особи
Семейство По алгоритму Вопрос по датчику случайных чисел Вопреки алгоритму
Capryophyllaceae 2 7 7
Ranunculaceae 3 5 4
Rosaceae 2 5 9

Видно явное превосходство действий пользователя в соответствии с рекомендациями программы, по сравнению с другими способами выбора признаков для диагностики одних и тех же растений.

Программа @RECOFAM внедрена в учебный процесс как учебное пособие (тренажер по курсу флористики) для студентов и аспирантов на кафедрах ботаники двух государственных педагогических университетов - Новосибирского и Омского.

Предложенный метод распознавания многомерных неопределенных объектов (ситуаций) по отношению к пересекающимся классам является весьма универсальным, поскольку очень многие реальные технические и научные объекты или понятия могут быть представлены совокупностью списковых значений количественных и качественных признаков. Ситуации ``не знаю'' по значению любого признака соответствуют в технологических задачах отказам каналов измерительной информации, поэтому применение разработанного алгоритма может значительно повысить надежность всей системы управления (идентификации). Многозначные классы объектов в различных задачах могут отражать наличие помех на фоне сигнала, разнообразие мнений экспертов о сложных ситуациях, группированные данные социологических опросов. То есть применение теории нечетких множеств открывает перспективы для алгоритмического решения задач обработки данных в сложных реальных условиях.

ЛИТЕРАТУРА

[1]
L.Zadeh Fuzzy Sets //Information and Control, 11(1965), N8, pp. 338-353.
[2]
S.Watanabe Modified Concepts of Logic, Probability and Information based on generalized Continuons Characteristic Function // Information and Control, 15 (1969), N1, pp. 22-32.
[3]
Ю.И.Журавлев Об алгебраическом подходе к решению задач распознавания или классификации // Проблемы кибернетики, вып.33. - М.:Наука, 1978. - С. 5-68.
[4]
В.И.Красинский Применение теории возможностей для ранжирования многозначных ботанических объектов // Автометрия, 1999, N3. - С. 65-81.
[5]
Shafer G. A Mathematical Theory of Evidence. Princeton: Princeton Univ. Press, 1976.
[6]
Дюбуа Д., Прад А. Теория возможностей. Приложения к представлению знаний в информатике. Пер. с фр. - М.:Радио и связь, 1990. 288 с.
[7]
Dubois D., Prade H. A set-theoretic view of belief functions. Logical operations and approximations by fuzzy sets // Int. J. of General Systems. 1986. 12(3). P. 193.
[8]
В.И.Красинский Предсказание ошибок в документах базы данных на основе нечеткого дескриптора по ключевым словам / V рабочее совещание по электронным публикациям EL-PUB2000. СО РАН, Новосибирск, 2000.
http://www-sbras.nsc.ru/ws/el-pub-2000/
[9]
И.М.Красноборов, В.И.Красинский Применение теории нечетких множеств для определения семейств растений // Доклады Академии наук, 2000. Том 374, N 4. - С. 565-567.
Ваши комментарии
[SBRAS]
[Головная страница]
[Конференции]
[СО РАН]

© 2001, Сибирское отделение Российской академии наук, Новосибирск
© 2001, Объединенный институт информатики СО РАН, Новосибирск
© 2001, Институт вычислительных технологий СО РАН, Новосибирск
© 2001, Институт систем информатики СО РАН, Новосибирск
© 2001, Институт математики СО РАН, Новосибирск
© 2001, Институт цитологии и генетики СО РАН, Новосибирск
© 2001, Институт вычислительной математики и математической геофизики СО РАН, Новосибирск
© 2001, Новосибирский государственный университет
Дата последней модификации Monday, 03-Sep-2001 12:56:06 NOVST