Язык спецификаций SIMPLE 1)

Ануреев И.С.
Институт систем информатики СО РАН

Аннотация

Предлагается новый язык спецификаций. Его основным достоинством является легкость изучения. Несмотря на простоту, язык обладает достаточной выразительной мощностью и имеет разрешающий метод для бескванторных формул. Описана методология применения языка для верификации программ на примере программы пузырьковой сортировки.

A new specification language is suggested. Its main advantage is an easiness of familiarization. In spite of simplicity the language has sufficient expressive power and has a satisfiability method for unquantified formulas. A methodology of application of the language for program verification is given by the example of a program of bubble sorting.

Введение

Практическое использование существующих систем верификации затруднено сложностью языков спецификаций, описывающих свойства программ. Язык спецификаций типичной системы верификации программ имеет большое количество часто неоднородных синтаксических конструкций, трудную для понимания семантику, требующую существенных познаний в логике, широкий спектр методов и техник автоматического доказательства, обширные библиотеки разрешающих процедур для конкретных теорий.

Освоение этого разнообразия средств языка спецификаций требует многих месяцев работы с системой. Только после этого можно решить, какие средства системы подходят наилучшим образом для верификации конкретного класса программ.

Часто оказывается, что из всего арсенала средств для рассматриваемого класса программ достаточно использовать одно или два, а изучение других средств оказывается потерянным временем.

В докладе представлен язык спецификаций SIMPLE, который можно освоить за один-два дня.

Он не является заменой серьезным языкам спецификаций, а скорее средством фильтрации программ. Критерий перехода к изощренным системам верификации - невозможность верифицировать программу, используя язык SIMPLE.

Несмотря на простоту, язык SIMPLE не игрушечный, а класс программ, которые можно верифицировать с его помощью, достаточно представителен. Таким образом, язык SIMPLE - это инструмент для улучшения производительности процесса верификации программ.

Язык спецификаций SIMPLE

Язык SIMPLE является двухсортным языком логики предикатов первого порядка с сортами "элемент" и "множество" и с единственным предикатным символом "принадлежать множеству".
Сигнатура
Cигнатура языка SIMPLE -- четверка $(F,\in,S,X)$, где $F$ -- множество функциональных символов, $\in$ -- предикатный символ "быть подмножеством", $S=\{Elem,Set\}$ -- множество сортов, $X$ -- множество переменных.

Каждому функциональному символу соответствует неотрицательное целое число -- его местность.

Множество функциональных символов разделяется на два непересекающихся подмножества детерминированных функциональных символов $F_d$ и недетерминированных фунциональных символов $F_u$. Множество детерминированных функциональных символов содержит символ неопределенности $\omega$.

Термы
Термы сигнатуры строятся обычным образом:

- если $x$ -- переменная, то $x$ -- терм;
- если $t_1,\ldots,t_n$ -- термы, $f\in F$, то $f(t_1,\ldots,t_n)$ -- терм.

Термы делятся на детерминированные и недетерминированные. Терм называется недетерминированным, если он содержит недетерминированный функциональный символ, иначе он называется детерминированным.

Формулы
Атомарные формулы имеют вид $t\in s$, где $t$ -- детерминированный терм, $s$ -- произвольный терм.

Формулы языка спецификаций SIMPLE строятся из атомарных формул с помощью пропозициональных логических связок и кванторов:

- если $A$ -- атомарная формула, то $A$ -- формула;
- $true$, $false$ -- формулы;
- если $A,B$ -- формулы, то $\neg(A)$, $A\wedge B$, $A\vee B$, $A\Rightarrow B$, $A\Leftrightarrow B$ -- формулы;
- если $x$ -- переменная, $A$ -- формула, то $\forall x(A)$ и $\exists x(A)$ -- формулы.

Семантика сигнатуры
Определим интерпретацию $I$ символов сигнатуры языка SIMPLE:

- $I(Elem)$ -- множество элементов;
- $I(Set)$ -- множество всех подмножеств из элементов множества $I(Elem)$;
- $I(\in)$ -- предикат принадлежности элемента множеству;
- если $f\in F_d$, $n$ -- местность $f$, то $I(f)$ -- тотальная функция из $(I(Elem))^n$ в $I(Elem)$;
- если $f\in F_u$, $n$ -- местность $f$, то $I(f)$ -- тотальная функция из $(I(Elem))^n$ в $I(Set)$.

Значением переменной $x\in X$ при интерпретации $I$ называется элемент множества $I(Elem)$. Функция $\phi_I$, сопоставляющая всем переменным множества $X$ их значения при интерпретации $I$, называется означиванием переменных при интерпретации $I$.

Семантика термов
Означивание $\phi_I$ расширяется на термы, отличные от переменных, следующим образом:

- если $t_1,\ldots,t_n$ -- термы, $f\in F_d$, то

\begin{displaymath}\phi_I(f(t_1,\ldots,t_n))=\{I(f)(a_1,\ldots,a_n)\vert a_1\in \phi_I(t_1),\ldots,a_n\in\phi_I(t_n)\};\end{displaymath}

- если $t_1,\ldots,t_n$ -- термы, $f\in F_u$, то


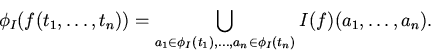
\begin{displaymath}\phi_I(f(t_1,\ldots,t_n))=\bigcup_{a_1\in\phi_I(t_1),\ldots,a_n\in \phi_I(t_n)}I(f)(a_1,\ldots,a_n).\end{displaymath}

Для детерминированных термов определим специальный вид означивания -- детерминированное означивание $\phi_I^d$:
- если $x$ -- переменная, то $\phi_I^d(x)=\phi_I(x)$;
- если $t_1,\ldots,t_n$ -- термы, $f\in F_d$, то $\phi_I^d(f(t_1,\ldots,t_n))=I(f)(\phi_I^d(t_1),\ldots,\phi_I^d(t_n))$.
Семантика формул
Определим семантику формул языка спецификаций SIMPLE.

Атомарная формула $t\in s$ истинна при интерпретации $I$ и означивании $\phi_I$, если $\phi_I^d(t)\in\phi_I(s)$. Атомарная формула $t\in s$ истинна при интерпретации $I$, если $\phi_I^d(t)\in\phi_I(s)$ для любого означивания $\phi_I$. Атомарная формула $t\in s$ истинна, если $\phi_I^d(t)\in\phi_I(s)$ для любой интерпретации $I$ и для любого означивания $\phi_I$. Атомарная формула $t\in s$ выполнима при интерпретации $I$, если $\phi_I^d(t)\in\phi_I(s)$ для некоторого означивания $\phi_I$.

С помощью атомарных формул выразимо отношение равенства элементов. Если $s$ -- детерминированный терм, то $t\in s$ означает равенство термов $t$ и $s$.

Семантика пропозициональных логических связок и кванторов определяется обычным образом.

Распространим выполнимость на множества и множества множеств бескванторных формул. Множество бескванторных формул $u$ выполнимо при интерпретации $I$, если формула $\wedge_{A\in u}A$ выполнима при интерпретации $I$. Множество множеств бескванторных формул $U$ выполнимо при интерпретации $I$, если формула $\vee_{u\in U}\wedge_{A\in u}A$ выполнима при интерпретации $I$. С помощью множеств множеств формул с такой семантикой будет задаваться дизъюнктивная нормальная форма для бескванторных формул.

Правила пополнения формул

Правила пополнения предназначены для пополнения множества формул и применяются для доказательства его невыполнимости. Если на некотором шаге пополнения множество формул содержит формулу и ее отрицание, то это множество формул невыполнимо. Правила пополнения формул составляют основу разрешающего метода для бескванторных формул языка SIMPLE. Способ пополнения задается отношением пополнения, порождаемым правилом пополнения формул. Ниже определяются правила пополнения формул четырех видов. Каждый последующий вид включает все предыдущие. Для каждого вида правил пополнения формул дается критерий сохранения выполнимости множества формул при его пополнении.

Для множества формул $u$ пусть $Var(u)$ обозначает множество переменных, входящих в формулы множества $u$. Для множеств формул $u_1,\ldots,u_n$ пусть $Var(u_1,\ldots,u_n)$ обозначает множество переменных $\cup_{1\leq i\leq n}Var(u_i)$.

Простые правила пополнения формул
Простое правило пополнения формул имеет вид $L\rightarrow R$, где $L,R$ -- множества формул такие, что $Var(R)\subseteq Var(L)$.

Пусть $\rho$ -- правило пополнения формул вида $L\rightarrow R$.

Отношение пополнения $\rightarrow_{\rho}$, порождаемое правилом $\rho$ определяется как множество пар $u\rightarrow u\cup\{r\sigma\ \vert\ r\in R\}$, где $u$ -- конечное множество формул, $\sigma$ -- подстановка такая, что $l\sigma\in u$ для любого $\l\in L$.

Предложение 1. Пусть для правила $\rho$ выполнено следующее условие:
- формула $\wedge_{l\in L}l\Rightarrow\wedge_{r\in R}r$ истинна при интерпретации $I$.

Пусть $u\rightarrow_{\rho}v$. Тогда $u$ выполнимо при интерпретации $I$ тогда и только тогда, когда $v$ выполнимо при интерпретации $I$.

Правила пополнения формул с разбором случаев
Правило пополнения формул с разбором случаев имеет вид

\begin{displaymath}L\rightarrow R_1,\ldots,R_n,\end{displaymath}

где $L,R_1,\ldots,R_n$ -- множества формул такие, что $Var(R_1,\ldots,R_n)\subseteq Var(L)$.

Пусть $\rho$ -- правило пополнения формул вида $L\rightarrow R_1,\ldots,R_n$.

Отношение пополнения $\rightarrow_{\rho}$, порождаемое правилом $\rho$ определяется как множество пар $u\rightarrow\{u\cup\{r\sigma\ \vert\ r\in R_1\},\ldots, u\cup\{r\sigma\ \vert\ r\in R_n\}\}$, где $u$ -- конечное множество формул, $\sigma$ -- подстановка такая, что $l\sigma\in u$ для любого $\l\in L$.

Предложение 2. Пусть для правила $\rho$ выполнено следующее условие:
- формула $\wedge_{l\in L}l\Rightarrow\vee_{1\leq i\leq n}\wedge_{r_i\in R_i}r_i$ истинна при интерпретации $I$.

Пусть $u\rightarrow_{\rho}V$. Тогда $u$ выполнимо при интерпретации $I$ тогда и только тогда, когда $V$ выполнима при интерпретации $I$.

Условные правила пополнения формул
Условное правило пополнения формул имеет вид

\begin{displaymath}P_1,\ldots,P_n\vert L\rightarrow R_1,\ldots,R_n,\end{displaymath}

где $P_1,\ldots,P_n,L,R_1,\ldots,R_n$ -- множества формул такие, что

\begin{displaymath}Var(P_1,\ldots,P_n,R_1,\ldots,R_n)\subseteq Var(L).\end{displaymath}

Пусть $\rho$ -- правило пополнения формул вида $P_1,\ldots,P_n\vert L\rightarrow R_1,\ldots,R_n$.

Отношение пополнения $\rightarrow_{\rho}$, порождаемое правилом $\rho$ определяется как множество пар $u\rightarrow\{u\cup\{p\sigma\ \vert\ p\in P_1\}\cup\{r\sigma\ \vert\ r\in R_1\},\ldots, u\cup\{p\sigma\ \vert\ p\in P_n\}\cup\{r\sigma\ \vert\ r\in R_n\}\}$, где $u$ -- конечное множество формул, $\sigma$ -- подстановка такая, что $l\sigma\in u$ для любого $\l\in L$.

Предложение 3. Пусть для правила $\rho$ выполнены следующие условия:
- формула $\wedge_{l\in L}l\Rightarrow\vee_{1\leq i\leq n}\wedge_{p_i\in P_i}p_i$ истинна при интерпретации $I$.
- формула $\wedge_{l\in L}l\wedge\wedge_{p_i\in P_i}p_i\Rightarrow\vee_{j\in J_i}\wedge_{r_j\in R_j}r_j$ истинна при интерпретации $I$ для каждого $1\leq i\leq n$. Здесь $J_i=\{j\vert p_j\ \mbox{совпадает с}\ p_i\ \mbox{и}\ 1\leq j\leq n\}$.

Пусть $u\rightarrow_{\rho}V$. Тогда $u$ выполнимо при интерпретации $I$ тогда и только тогда, когда $V$ выполнимо при интерпретации $I$.

Правила пополнения формул с экстра-переменными
Правило пополнения с экстра-переменными формул имеет вид

\begin{displaymath}P_1,\ldots,P_n\vert L\rightarrow R_1,\ldots,R_n,\end{displaymath}

где $P_1,\ldots,P_n,L,R_1,\ldots,R_n$ -- множества формул такие, что

\begin{displaymath}Var(R_1,\ldots,R_n)\subseteq Var(L,P_1,\ldots,P_n).\end{displaymath}

Ограничение, что переменные, входящие в $P_1,\ldots,P_n$, входят также в $L$, убирается. Формулы, входящие в множества $P_1,\ldots,P_n,R_1,\ldots,R_n$ могут содержать экстра-переменные.

Пусть $\rho$ -- правило пополнения формул вида $P_1,\ldots,P_n\vert L\rightarrow R_1,\ldots,R_n$.

Отношение пополнения $\rightarrow_{\rho}$, порождаемое правилом $\rho$ определяется как множество пар $u\rightarrow\{u\cup\{p\tau\sigma\ \vert\ p\in P_1\}\cup\{r\tau\sigma\ \vert\ r\... ...s, u\cup\{p\tau\sigma\ \vert\ p\in P_n\}\cup\{r\tau\sigma\ \vert\ r\in R_n\}\}$, где $u$ -- конечное множество формул, $\sigma$ -- подстановка такая, что $l\sigma\in u$ для любого $\l\in L$, $\tau$ -- подстановка, заменяющая экстра-переменные правила $\rho$ на новые переменные, не содержащиеся в $u$.

Предложение 4. Пусть для правила $\rho$ выполнены следующие условия:
- формула $\wedge_{l\in L}l\Rightarrow\vee_{1\leq i\leq n}\exists \bar{x}_i\wedge_{p_i\in P_i}p_i$, где $\bar{x}_i$ -- экстра-переменные, входящие в формулы множества $P_i$, истинна при интерпретации $I$.
- формула $\wedge_{l\in L}l\wedge\wedge_{p_i\in P_i}p_i\Rightarrow\vee_{j\in J_i}\wedge_{r_j\in R_j}r_j$ истинна при интерпретации $I$ для каждого $1\leq i\leq n$. Здесь $J_i=\{j\vert p_j\ \mbox{совпадает с}\ p_i\ \mbox{и}\ 1\leq j\leq n\}$.

Пусть $u\rightarrow_{\rho}V$. Тогда $u$ выполнимо при интерпретации $I$ тогда и только тогда, когда $V$ выполнимо при интерпретации $I$.

Системы пополнения формул
Правила пополнения формул с экстра-переменными -- самый общий вид правил пополнения формул. В дальнейшем, под правилами пополнения формул понимаются правила самого общего вида.

Распространим правила пополнения формул на множества множеств формул.

Отношение пополнения $\rightarrow_{\rho}$, порождаемое правилом $\rho$ определяется как множество пар $U\rightarrow_{\rho}U\setminus\{u\}\cup W$, где $u\in U$, $u\rightarrow_{\rho}W$.

Система пополнения формул -- это множество правил пополнения формул.

Отношение пополнения для системы пополнения формул определяется как объединение отношений для правил пополнения формул, входящих в систему.

Выразительные возможности правил пополнения

Правила пополнения формул позволяют в едином формализме выразить широко используемые техники проверки выполнимости формул такие, как вывод следствий из аксиом, переписывание термов, проведение разбора случаев, выполнение упрощающих замен переменных.
Вывод следствий из аксиом
Вывод следствий из аксиом представляется в виде простых правил пополнения формул. Применению аксиомы $A_1\wedge\ldots\wedge A_n\Rightarrow A$ соответствует применение правила

\begin{displaymath}\{A_1,\ldots,A_n\}\rightarrow\{A\}.\end{displaymath}

Правила переписывания термов
Правило переписывания термов $l\rightarrow r$ представимо в виде $\{x\in l\}\rightarrow\{x\in r\}$, где $x$ -- новая переменная, не встречающаяся в $l,r$.

Проблем с коммутативными и ассоциативными правилами не возникает. Например, правило переписывания термов $x+y\rightarrow y+x$ приводит к зацикливанию, в то время как соответствующее правило пополнения $\{z\in x+y\}\rightarrow\{z\in y+x\}$ нет.

Аналог условного правила переписывания термов $A_1\wedge\ldots\wedge A_n\vert l\rightarrow r$ в случае, когда $A_1,\ldots,A_n$ -- нормализованные литералы, имеет вид $\{A_1,\ldots,A_n\}\vert\{x\in l\}\rightarrow\{x\in r\}$, где $x$ -- новая переменная, не встречающаяся в $A_1,\ldots,A_n,l,r$.

Разбор случаев
Разбор случаев представляется в виде правил пополнения формул с разбором случаев. Разбор случаев $A_1\vee\ldots\vee A_n\Rightarrow A$, проводимый при выполнении условия $A$, соответствует применению правила

\begin{displaymath}\{A\}\rightarrow\{A_1\},\ldots,\{A_n\}.\end{displaymath}

Замена переменных
Замена переменных представляется в виде правил пополнения формул с экстра-переменными. Замена переменных $x_1\rightarrow t_1,\ldots,x_n\rightarrow t_n$, проводимая при выполнении условия $A$, соответствует применению правила

\begin{displaymath}\{x_1\in t_1,\ldots,x_n\in t_n\}\vert\{A\}\rightarrow\{true\}.\end{displaymath}

Метод разрешения бескванторных формул языка SIMPLE

Метод проверки выполнимости формул языка SIMPLE применяется к бескванторным формулам этого языка.

Он основан на специальном (нормализованном) представлении литералов в дизьюнктивной нормальной форме и применении правил пополнения к дизьюнктивной нормальной форме с нормализованными литералами.

Нормализованные литералы
Нормализованным литералом называется литерал вида
$x\in f(x_1,\ldots,x_n)$ или $\neg(x\in f(x_1,\ldots,x_n))$,
где $x,x_1,...,x_n$ -- переменные, $f$ -- функциональный символ.
Алгоритм приведения к дизьюнктивной нормальной форме с нормализованными литералами
Пусть $v$ -- множество формул, $V$ -- множество множеств формул.

Алгоритм приведения формул языка к дизьюнктивной нормальной форме с нормализованными литералами заключается в недетерминированном применении к обычной дизьюнктивной нормальной форме, представленной в виде множества множеств формул, следующих правил:
- $\{v\cup\{s\in f(t_1,\ldots,t_{i-1},t_i,t_{i+1},\ldots,t_n)\}\}\cup V$ где $t_i$ -- не переменная, заменяется на

\begin{displaymath}\{v\cup\{y\in t_i,s\in f(t_1,\ldots,t_{i-1},y,t_{i+1},\ldots,t_n)\}\}\cup V,\end{displaymath}

где $y$ -- новая переменная, не встречающаяся в $u$;
- $\{v\cup\{s\in t\}\}\cup V$, где $s$ -- не переменная, заменяется на $\{v\cup\{y\in s,y\in t\}\}\cup V$, где $y$ -- новая переменная, не встречающаяся в $u$.

Предложение 5. Пусть $V$ -- дизъюнктивная нормальная форма с нормализованными литералами для бескванторной формулы $A$. Тогда $V$ выполнимо при интерпретации $I$ тогда и только тогда, когда $A$ выполнима при интерпретации $I$.

Метод разрешения бескванторных формул языка SIMPLE
Метод разрешения бескванторных формул языка SIMPLE является проблемно-ориентированным и состоит из следующих шагов:

Пусть $A$ -- бескванторная формула, проверяемая на выполнимость.

Шаг 1. Приводим формулу $A$ к дизъюнктивной нормальной форме с нормализованными литералами.

Пусть $V$ -- дизъюнктивная нормальная форма с нормализованными литералами для формулы $A$, $R$ -- пустая система пополнения формул (пустое множество правил пополнения формул).

Шаг 2. Расширяем систему $R$ правилами для понятий (интерпретированных функциональных символов), входящих в $A$. Формулы, входящие в правила системы $R$ должны быть нормализованными литералами.

Шаг 3. Применяем приведенные ниже правила в указанном порядке до тех пор, пока применимо хотя бы одно правило:
- $\{\{false\}\cup v\}\cup V$, где $V\not =\emptyset$, заменяется на $V$;
- $\{\{false\}\cup v\}$, заменяется на $\{\{false\}\}$;
- $\{\{true\}\cup v\}\cup V$, где $v\not =\emptyset$, заменяется на $\{v\}\cup V$;
- $\{\{true\}\}\cup V$, заменяется на $\{\{true\}\}$;
- $\{\{B,\neg(B)\}\cup v\}\cup V$ заменяется на $\{\{false\}\cup v\}\cup V$;
- $\{\{x\in x\}\cup v\}\cup V$ заменяется на $\{v\}\cup V$;
- eсли $\{x\in t,y\in t\}\subseteq u$, где $t\in F_d$, то $\{v\}\cup V$ заменяется на $\{v[x\leftarrow y]\}\cup V$;
- $\{\{x\in y\}\cup v\}\cup V$, где $x,y$ -- переменные, заменяется на $\{v[x\leftarrow y]\}\cup V$;
- eсли $V\rightarrow_{R}W$, то $V$ заменяется на $W$.

Шаг 4. Если $V$ имеет вид $\{\{true\}\}$ или $\{\{false\}\}$, то КОНЕЦ с результатом $V$. В противном случае, перейти к шагу 2.

Метод позволяет проверять невыполнимость формул. Его можно использовать также в качестве упрощающего метода, если ограничить число повторений шагов 2 и 3. Множество $V$, полученное поcле $k$ выполнений шагов 2 и 3, называется $k$-м упрощением формулы $A$.

Предложение 6. Пусть $V$ -- результат применения алгоритма разрешения бескванторных формул языка SIMPLE к формуле $A$. Тогда $V$ выполнимо при интерпретации $I$ тогда и только тогда, когда $A$ выполнима при интерпретации $I$.

Методология использования языка SIMPLE при верификации программ

Опишем методологию использования языка SIMPLE для верификации программ на примере программы пузырьковой сортировки массива.
Средства аннотации программы
Для аннотирования программы в язык SIMPLE вводятся следующие понятия:

1.Для массивов (ниже $a$ -- массив, $n,m$ -- целые числа):
- $a[n,m]$ -- кортеж из элементов массива от $n$-го до $m$-го. Если $n>m$, результатом является пустой кортеж;
- $a[n]$ -- $m$-й элемент массива $a$ (нумерация начинается с нуля). Если $n<0$, то $a[n]=\omega$.

2. Для кортежей (ниже $x$ -- кортеж ) определены понятия $perm,\ ord,\ <=$ такие, что:
- $perm(x)$ -- множество кортежей, перестановочных с $x$;
- $ord$ -- множество упорядоченных кортежей;
- $<=(x)$ -- множество кортежей, любой элемент которых меньше или равен любого элемента кортежа $x$;

3. Для целых чисел (ниже $n,m$ -- целые числа) определены понятия $<=,\ <,\ >=,\ >,\ +,\ -,\ 0,\ 1,\ 2,\ \ldots$ такие, что:
- $<=(n)$ -- множество элементов, меньших или равных $n$;
- $<(n)$ -- множество элементов, меньших $n$;
- $>=$ и $>$ определяются аналогично;
- $n+m,n-m$ -- сумма и разность $n$ и $m$, соответственно.

Заметим, что предикаты в языке SIMPLE представляются недетерминированными функциями. Так предикату упорядоченности элементов кортежа соответствует недетерминированная функция $ord$, значением которой является любой упорядоченный кортеж, а предикату перестановочности кортежей -- недетерминированная функция $perm$, которая выдает в качестве значения любой кортеж, перестановочный с кортежем-аргументом функции.

Еще одно замечание заключается в том, что для массивов, кортежей и целых чисел не определяется равенство, так как оно, как уже было отмечено выше, встроено в предикат $\in$.

Аннотированная программа
Аннотированная программа имеет вид

$pred$ ${\bf for(int\ i=2;i<=n;i++)}$
$inv1\ {\bf for(int\ j=n;j>=i;i--)}$
$inv2\ {\bf if(a[j-1]>a[j]) \{x=a[j-1]; a[j-1]=a[j]; a[j]=x\}}$
$post$

Жирным шрифтом выделены строки кода на языке C, $pred$, $post$, $inv1$, $inv2$ -- формулы на языке SIMPLE, задающие предусловие, постусловие, инвариант внешнего цикла и инвариант внутреннего цикла соответственно.

Предусловие $pred$ имеет вид $a[1,n]\in b\wedge n\in >=(1)$.

Постусловие $post$ имеет вид $a[1,n]\in perm(b)\wedge a[1,n]\in ord$.

Инвариант $inv1$ имеет вид $n\in >=(1)\wedge a[1,n]\in perm(b)\wedge a[1,i-1]\in ord\wedge$ $a[1,i-2]\in <=(a[i,n])\wedge i\in >=(2)\wedge i\in <=(n+1))$.

Инвариант $inv2$ имеет вид

\begin{displaymath}inv1\wedge a[j,j]\in <=(a[j+1,n])\wedge j\in <=(n)\wedge j\in >=(i-1).\end{displaymath}

Условия корректности
С помощью метода Хоара-Флойда генерируются 6 условий корректности:
- $pred\Rightarrow (inv1[i\leftarrow 2])$;
- $inv1\wedge i\in <=(n)\Rightarrow (inv2[j\leftarrow n])$;
- $inv1\wedge \neg (i\in <=(n))\Rightarrow post$;
- $inv2\wedge j\in >=(i)\wedge a[j-1]\in >(a[j])\Rightarrow (inv2[a\leftarrow upd(upd(a,j-1,a[j]),j,a[j-1]),j\leftarrow j-1])$;
- $inv2\wedge j\in >=(i)\wedge \neg (a[j-1]\in >(a[j]))\Rightarrow (inv2[j\leftarrow j-1])$;
- $inv2\wedge \neg (j\in >=(i))\Rightarrow (inv1[i\leftarrow i+1])$.

Заметим, что если аннотации были бескванторными формулами, то условия корректности (при определенных ограничениях на язык программирования) также будут бескванторными формулами.

Доказательство условий корректности
Доказательство условий корректности заключается в применении разрешающего метода для бескванторных формул языка SIMPLE к отрицаниям условий корректности. Истинность условия корректности соответствует невыполнимости его отрицания.

Для применения метода необходимо задать правила пополнения для понятий, входящих в условия корректности. Вот несколько примеров правил пополнения для понятий $perm$, $ord$ и $<=$, определенного на кортежах:
- $x[i,j]\in y\Rightarrow x[i,j]\in perm(y)$;
- $upd(upd(a,j-1,a[j]),j,a[j-1])[1,n]\in perm(b)\Rightarrow a[1,n]\in perm(b)$;
- $a[i,i]\in ord\Rightarrow true$; $x[1,0]\in <=(y)\Rightarrow true$; $x\in <=(y[n+1,n])\Rightarrow true$.

Кроме того, имеется ряд правил пополнения для арифметики, например $i\in >=(i)\Rightarrow true$. Если комбинировать метод разрешения бескванторных формул языка SIMPLE с разрешающей процедурой для арифметики Пресбургера, то необходимость в этих правилах отпадает.

Если невыполнимость всех отрицаний условий корректности доказана, то исходная аннотированная программа корректна.

Локализация ошибки
Если после $k$-го применения шагов 2 и 3 разрешающего метода к проверяемой формуле новые правила не добавляются, то $k$-е упрощение этой формулы задает контрпример -- ограничение на входные данные программы, при которых ее выполнение может оказаться некорректным. Представление этого ограничения в виде дизъюнктивной нормальной формы с нормализованными литералами позволяет легко отследить возможную ошибку в программе (или аннотациях).

Заключение

В работе получены следующие результаты:
- Предложен новый язык спецификаций SIMPLE, сочетающий простоту с достаточной выразительной мощностью;
- Разработан новый метод автоматического доказательства -- системы пополнения формул, комбинирующие и унифицирующие такие известные техники и приемы автоматического доказательства, как вывод следствий, переписывание термов, разбор случаев и замена переменных;
- Дан метод разрешения бескванторных формул языка SIMPLE;
- Описана методология применения языка SIMPLE для верификации программ.

Примечание

. . . SIMPLE1
Работа частично поддержана грантами РФФИ 00-01-00909, РФФИ 01-01-06141 и молодежным грантом президиума СО РАН.
Ваши комментарии
[SBRAS]
[Головная страница]
[Конференции]
[СО РАН]

© 2001, Сибирское отделение Российской академии наук, Новосибирск
© 2001, Объединенный институт информатики СО РАН, Новосибирск
© 2001, Институт вычислительных технологий СО РАН, Новосибирск
© 2001, Институт систем информатики СО РАН, Новосибирск
© 2001, Институт математики СО РАН, Новосибирск
© 2001, Институт цитологии и генетики СО РАН, Новосибирск
© 2001, Институт вычислительной математики и математической геофизики СО РАН, Новосибирск
© 2001, Новосибирский государственный университет
Дата последней модификации Tuesday, 28-Aug-2001 21:47:31 NOVST