Метод упругих функций 1

Нартов Б.К.
Омский филиал института математики им. С.Л. СоболеваСО РАН, Омск

Аннотация:

В работе представлены возможности нового метода формализации траекторных задач в виде задач оптимального управления.

In the paper are presented the new method`s possibilities of the formalization of the path (trajectory`s) problems in the form of the optimal control problems.

Разработку метода упругих функций стимулировала известная задача планирования поиска на плоскости неподвижных целей с заданными функциями плотностей распределения вероятностей [4]. Долгое время не удавалось свести эту задачу к классическим задачам условной оптимизации. Основную проблему представлял аналитический учет пересечений и самопересечений полос поиска - непереборные решения строились лишь для частных случаев или получались при дополнительных ограничениях на управление поисковыми единицами. Предложенный нами в [1-3] подход решает эту проблему и позволяет формально просто записать общий случай планирования поиска в виде задачи оптимального управления.

Существенно, что предметная область найденного подхода оказалась много шире задач поиска стационарных объектов. Например, в задачах преследования целей с заданными траекториями метод упругих функций позволяет аналитически запоминать моменты первых касаний целей объектами - преследователями и сколь угодно точно ``затормаживать'' движения коснувшихся пар. Таким образом, удается избавиться от дифференциальных уравнений траекторий объектов - преследователей, обойти комбинаторные трудности и свести общий случай исходной задачи к классической задаче условной оптимизации. В контексте представляемого метода удалось формализовать в виде стандартных задач оптимального управления и некоторые задачи дискретной оптимизации, например задачу коммивояжера, интерпретируемую предварительно как ``задачу преследования неподвижных целей''.

За недостатком места мы опускаем проведенные доказательства и описания верифицирующих экспериментов, ограничиваясь ниже по возможности наглядными примерами, представляющими три контрастных класса задач траекторного управления.


Преследование подвижных целей

Задача 1 (простейший случай). Задан временной интервал $[0, t_{f}]$, траектория цели $\bar {a}(t)$, $0 \le t \le t_{f}$, в евклидовом пространстве $Е^{3}$, начальная координата объекта-преследователя $\bar {x}(0)$, динамические и пространственные ограничения на его возможные траектории $\bar{x}(\cdot)$, выражающиеся в системе неравенств, связывающих функцию $\bar {x}(t)$ и ее производные до второй включительно.

Требуется формализовать задачу вычисления траектории $\bar {x}^{\ast} ( \cdot)$, оптимальной в смысле задачи

\begin{displaymath}t_{\varsigma}\to inf, \eqno (1)\end{displaymath}

где $t_{\varsigma}$- момент захвата цели, а именно минимальное решение неравенства $\vert \bar {x}(t) - \bar {a}(t)\vert \, < \,\varepsilon _{1} $, принадлежащее $[0, t_{f}]$, где $\varepsilon _{1}$ задано.

Решение. Обозначив $\bar {r}(t) = \bar {x}(t) - \bar {a}(t)$, введем (рис.1) первую вспомогательную функцию $F(s(t)),\,s(t) = \vert \bar {r}(t)\vert$, удовлетворяющую трем условиям:

1. $F(s)$ дифференцируема.
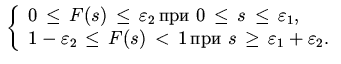
2. $\,{\left\{ {\begin{array}{l} {0\, \le \,F(s)\, \le \,\varepsilon _{2}\, \mbox{... ...,s\, \ge \,\varepsilon _{1} + \varepsilon _{2} .} \\ \end{array}} \right.} $
3. Значения $\varepsilon $$_{1}$ и $\varepsilon $$_{2}$ регулируются параметрами функции $F(s)$ независимо (в смысле неравенств 0 < $\varepsilon $$_{2}$< $\varepsilon $$_{1}$ и 0 < $\varepsilon $$_{1}$< $\varepsilon $$_{3}$, где $\varepsilon $$_{3}$ - заданное число).

Figure: Вспомогательная функция $F(S)$
\begin{figure}\begin{center} \epsfxsize=12cm \epsfysize=12cm\epsfbox{r1.eps} \end{center}\end{figure}

Конкретный вид $F(s)$, удовлетворяющей этим условиям, вполне произволен.

Попытаемся теперь подобрать дифференцируемую функцию $\tilde {F}(s( \cdot ),t)$, которая для любого интервала (0 $, t) \quad \subset $ (0$,$) сколь угодно точно (регулировкой параметров функций $\tilde {F}$ и $F)$ приближает значения функции $F_{1} (s( \cdot ),t) = {\mathop {inf}\limits_{0 \le \tau \le t}} F(s(\tau ))$ при условии $\tilde {F}$ ($s$($ \cdot $)$,$0)=1.

Можно показать, что простейшая удовлетворяющая этим требованиям функция $\tilde {F}(s( \cdot ),t)_{}$ является решением дифференциального уравнения


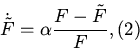
\begin{displaymath} \dot{\tilde {F}} = \alpha {\frac{{F - \tilde {F}}}{{F}}}, \eqno (2)\end{displaymath}

где $\alpha $ - регулируемый положительный параметр.

Физически уравнение (2) обусловливает следующие свойства функции $\tilde {F}$ (s($ \cdot )$,$t):$

$\tilde {F}$ ``достаточно быстро'' убывает по $t$ при $F < \tilde {F};$

$\tilde {F}$ ``достаточно медленно'' возрастает по $t$ при $F >\tilde {F}.$

Введем для функции $\tilde {F}$естественный термин ``упругая'' функция, а для функции $F$ - ``трафаретная'' функция.

Обратимся теперь к рис.2 , иллюстрирующему преобразование $s(t) \quad \to $ $F(s(t))$ $ \to $ ($s$($ \cdot $)$,t),$ и запишем приближенное решение исходной задачи в виде

Figure: Исходные данные в задачах поиска
\begin{figure}\begin{center} \epsfxsize=12cm \epsfysize=12cm\epsfbox{r2.eps} \end{center}\end{figure}


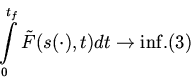
\begin{displaymath} {\int\limits_{0}^{t_{f}} {\tilde {F}(s( \cdot ),t)dt \to \inf }}.\eqno(3) \end{displaymath}

Решая уравнение (2) с начальным условием $\tilde {F}$ ($s( \cdot )$,0) = 1, получим


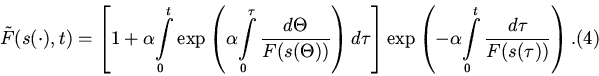
\begin{displaymath} \tilde {F}(s( \cdot ),t) = {\left[ {1 + \alpha {\int\limits_... ..._{0}^{t} {{\frac{{d\tau}} {{F(s(\tau ))}}}}}} \right).\eqno(4) \end{displaymath}

Подставляя (4) в (3), получаем классическую задачу вариационного исчисления. Фактически в (3) используется следующая интерпретация ``упругой'' функции$\tilde {F}$:


\begin{displaymath}{\frac{{d\tilde {t}}}{{dt}}} = \tilde {F}(s( \cdot )t),\eqno (5) \end{displaymath}

где $\tilde {t}$- новая переменная - ``управляемое'' время ($\tilde {t}$(0) = 0). Можно доказать, что для любых параметров и начальных условий задачи 1 всегда найдутся такие конкретные параметры функций $F$ и$\tilde {F}$, что функция $\tilde {t}(t_{f})$ из решения (3) сколь угодно точно приблизит момент захвата цели $t_{\varsigma}$(если, разумеется, захват вообще возможен - в противном случае $\tilde {t}(t_{f})$ с заданной точностью совпадает с $t_{f} )$.

Практически случай одной цели и одного преследователя, разумеется, легко разрешим стандартными средствами и рассмотрен здесь лишь в качестве иллюстрации. Однако предлагаемый подход позволяет формализовать и многие общие случаи задач оптимального преследования, например

Задачу 2. Задан временной интервал [0, $t_{f} $], траектории целей $\bar {a}_{i} (t)$, 0 $ \le $ t $ \le $ t$_{f}$, 1 $ \le $ i $ \le $ M, в евклидовом пространстве $E^{3}$, начальные координаты объектов-преследователей $\bar {x}_{j} (0), $1 $ \le $ j $ \le $ N, динамические и пространственные ограничения на их возможные траектории $\bar {x}_{j} ( \cdot ).$

Требуется формализовать задачу вычисления траекторий $\bar {x}_{j}^{ *} ( \cdot ), $1 $ \le $ j $ \le $ N, оптимальных в смысле минимизации суммарного времени жизни целей на интервале [0$,t_{f}$]. Если цель захвачена каким-либо объектом-преследователем (см. задачу 1), ее время жизни равно времени захвата, в противном случае время жизни цели совпадает со значением $t_{f}.$ При этом объект-преследователь, захвативший какую-либо цель, вычеркивается из дальнейшего рассмотрения.

Заметим, что схему решения задачи 1 нельзя тривиально распространить на общий случай. Необходимо, например, исключить следующие версии:

``атаку'' одной цели многими объектами-преследователями;

последовательные ``атаки'' многих целей одним объектом-преследователем.

Учет подобных ограничений в функционале качества [3] существенно усложняет реализующий алгоритм.


Поиск стационарных объектов

Исходные данные рассматриваемых в этой главе задач таковы. Односвязной области $G \subset E^{2}$достоверно принадлежат $К$ неподвижных целей с известными функциями плотностей распределения вероятностей $f_{k} (x),1 \le k \le K$, $x = (x_{1,\,} x_{2} ) \in [G]$, где [$G$] - замыкание области $G$. В замыкании [$G$] произвольным образом расположены в начальный момент времени $t=$0 $N$ поисковых единиц (ПЕ). При движении каждая ПЕ является центром окружности радиуса $а$, заметающей в области $G$ полосу шириной 2$а$ - ``полосу захвата''; попавшая в полосу цель считается обнаруженной (рис. 3).

Figure: Исходные данные в задачах поиска
\begin{figure}\begin{center} \epsfxsize=12cm \epsfysize=12cm\epsfbox{r3.eps} \end{center}\end{figure}


Введем следующие обозначения:

$\xi _{i} (t) = (\xi _{1} ^{i}(t),\xi _{2} ^{i}(t))$ - траектория i-й ПЕ, $1 \le i \le N,0 \le t \le t_{f} ,$

$t_{f} $ - время поиска;

$\tilde {K} = \tilde {K}({\left\{ {\xi _{i} (t),\vert 0 \le t \le t_{f} ,1 \le i \le N} \right\}},t)$ - случайная величина - количество целей, обнаруженных на интервале времени (0,$t)$, соответствующее стратегии поиска $u = \{\xi _{i} (t)\vert 0 \le t \le t_{f} ,1 \le i \le N\}$.

Считая реальные состояния поиска на заданном интервале (0,$t_{f} )$ неизвестными, сформулируем следующую задачу: при заданных ограничениях на управления ПЕ вычислить стратегию поиска $u^{ *} = \{\xi _{i} ^{ * }(t)\vert 0 \le t \le t_{f} ,1 \le i \le N\}$, максимизирующую математическое ожидание количества целей $M[\tilde {K}(u,t_{f} )]$, обнаруживаемых за время поиска $t_{f} $.

Рассмотрим функцию


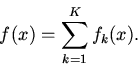
\begin{displaymath}f(x) = {\sum\limits_{k = 1}^{K} {f_{k} (x).}}\end{displaymath}

Очевидно


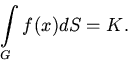
\begin{displaymath} {\int\limits_{G} {f(x)dS = K}}. \end{displaymath}

Обозначим $u(t) = \{\xi _{i} (\tau )\vert 0 \le \tau \le t,\,1 \le i \le N\}$, $u(t_{f} ) = u$. В каждый момент времени $t \in (0,t_{f} )$ множеству траекторий $u(t)$ соответствует объединение полос захвата ПЕ $G_{1}(u(t))$$.$ Обозначим теперь $G(u(t)) = G\backslash G_{1} (u(t))$ и $\Delta G_{1} (u(t)) = G_{1} (u(t + \Delta t))\backslash G_{1} (u(t)).$

Отсюда и из определения функции $f(x)$ и математического ожидания $M[\tilde {K}(u,t)]$ следует:


\begin{displaymath} \Delta M[\tilde {K}(u,t)] = {\int\limits_{\Delta G_{1} (u(t))} {f(x)dS}}. \eqno (6) \end{displaymath}

Теперь исходную задачу можно записать в виде


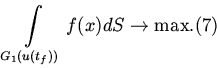
\begin{displaymath}\int\limits_{G_{1} (u(t_{f} ))} {f(x)dS \to \max}.\eqno(7)\end{displaymath}

Из (6) очевидно, что при планировании слепого поиска необходим учет пересечений и самопересечений полос захвата ПЕ, составляющий основную проблему формализации (7) в виде задачи оптимального управления.

Предлагаемое ниже решение основано на описанном в предыдущем разделе механизме ``упругих'' функций $\tilde {F}$, задаваемых, однако, в другом виде.

Определим предварительно на области G вспомогательную функцию $\lambda $, связанную с координатами ПЕ,


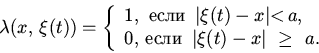
\begin{displaymath} \lambda (x,\,\xi (t)) = {\left\{ {\begin{array}{l} {1,\,\,\... ...t \xi (t) - x\vert \,\, \ge \,\,a.} \\ \end{array}} \right.} \end{displaymath}

Зададим далее дифференцируемую колоколообразную функцию $F(x, \xi (t))$, сколь угодно точно приближающую значения $\lambda $. Конкретный вид $F$ вполне произволен. См. рис.4.

Figure: Функции $\lambda $ и $F$
\begin{figure}\begin{center} \epsfxsize=12cm \epsfysize=12cm\epsfbox{r4.eps} \end{center}\end{figure}

Рассмотрим теперь функцию $\tilde {F}(x,\,u,\,t)$ , являющуюся решением дифференциального уравнения


\begin{displaymath} \dot {\tilde {F}} = \alpha {\sum\limits_{i = 1}^{N} {{\frac{{F_{i} - \tilde {F}}}{{1 - F_{i}}} }}}, \eqno (8) \end{displaymath}

где $\alpha $ - регулируемый положительный параметр; $\tilde {F}(x, u$, $0)=0.$

Можно показать, что для любых начальных условий исходной задачи всегда найдутся такие $F_{i}$ и $F$, что к моменту окончания поиска $t_{f} $ функция $\tilde {F}$ реализует над областью поиска $G$ дифференцируемый профиль, повторяющий движения ПЕ. При этом высота профиля с заданной точностью будет равна единице над просмотренными областями, в том числе и над областями пересечений и самопересечений полос поиска (захвата), и с заданной точностью равна нулю вне просмотренных областей. Это полезное свойство $\tilde {F}$ позволяет формализовать исходную задачу поиска (7) в виде


\begin{displaymath} J(u) = {\int\limits_{G} {f(x)\tilde {F}(x,\,u,\,t_{f} )dS \to \max ,}} \eqno (9)\end{displaymath}

то есть получить функционал с дифференцируемым интегралом, учитывающим любое возможное наложение поле захвата ПЕ.

Фактически относительно (9) утверждается следующее:

Для любых параметров и начальных условий исходной задачи и любого $\varepsilon $ >0 найдутся такие F$_{{\rm i}}$ и $\tilde {F}$, что (9) формализует задачу (7) для некоторого набора плотностей вероятностей $\tilde {f}_{k} (x)$, ${\rm 1} \le k \le K$, из интервала $\vert f_{k} (x) - \tilde {f}_{k} (x)\vert < \varepsilon ,$ где $f_{k} (x)$- исходные плотности вероятностей.

В [3] по подобной схеме мы формализовали и некоторые задачи управления поиском в реальном масштабе времени, когда известны моменты обнаружения и координаты обнаруживаемых целей. Заметим здесь, что вопросы о цене представления $\tilde {F}$в реализующем алгоритме и устойчивости траекторий ПЕ относительно точности приближения$f_{k} (x)$требуют отдельного обсуждения.


Дискретная оптимизация

Используя результаты раздела 1, интерпретируем задачу коммивояжера как ``задачу оптимального преследования неподвижных целей'', а именно как задачу минимизации времени захвата последней из $N$ неподвижных целей одним неуничтожаемым объектом-преследователем.

Figure: К задаче коммивояжера. $t_{1} ,\,...\,,\,t_{N}$ - моменты $\varepsilon $ - касаний пунктов ${\rm 1}{\rm ,} {\rm \ldots} , N$ Динамика запасов растительного вещества
\begin{figure}\begin{center} \epsfxsize=12cm \epsfysize=14cm\epsfbox{r5.eps} \end{center}\end{figure}

Обозначим:

$\bar {x}_{i} ,\,i = \overline {1,\,N} $ - координата $i$-го пункта;

$\bar {x}(t)$ - координата коммивояжера, где $\bar {x}(0)$ задана;

$F$ и $\tilde {F}$ - трафаретная и упругая функции - в том виде, в котором они определены в модели оптимального поиска в разделе 2 (случай одной поисковой единицы);

L - длина минимального маршрута.

Запишем задачу


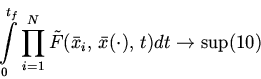
\begin{displaymath} {\int\limits_{0}^{t_{f}} {{\prod\limits_{i = 1}^{N} {\tilde ... ...{x}_{i} ,\,\bar {x}( \cdot ),\,t)dt \to \sup}} } } \eqno (10) \end{displaymath}


с ограничением на управление


\begin{displaymath} \vert \dot {\bar {x}}(t)\vert \, \le \,V,t \in (0,t_{f} ). \end{displaymath}

Далее легко показать, что при условии $Vt_{f} > L$ для любого $\varepsilon \, > \,0$ найдутся такие F и $\tilde {F}$, что решение (10) обеспечивает $\varepsilon $-близкий и, с точностью до$N\varepsilon $, оптимальный обход пунктов. См. рис. 5


Литература

1
Nartov B.K. Conflict of Moving Systems. - AMSE Press, France, 1994. - 87 p.

2
Нартов Б.К. и др. Конфликт сложных систем. Модели и управление. - М.: Изд-во МАИ, 1995. - 120 с.

3
Нартов Б.К., Чуканов С.Н. Модели траекторного управления. - Омск: Изд-во ОмГУ, 2001. - 100 с.

4
Хеллман О. Введение в теорию оптимального поиска. - М.: Наука, 1985. - 254 с.

Примечание

... функций1
Работа выполнена при поддержке РФФИ, проекты 01-01-00303, 01-07-90003
Ваши комментарии
[SBRAS]
[Головная страница]
[Конференции]
[СО РАН]

© 2001, Сибирское отделение Российской академии наук, Новосибирск
© 2001, Объединенный институт информатики СО РАН, Новосибирск
© 2001, Институт вычислительных технологий СО РАН, Новосибирск
© 2001, Институт систем информатики СО РАН, Новосибирск
© 2001, Институт математики СО РАН, Новосибирск
© 2001, Институт цитологии и генетики СО РАН, Новосибирск
© 2001, Институт вычислительной математики и математической геофизики СО РАН, Новосибирск
© 2001, Новосибирский государственный университет
Дата последней модификации Monday, 10-Sep-2001 17:11:53 NOVST