Создан 24 мая 1964 г.
Адрес: 630090 Новосибирск, просп. Академика М.А. Лаврентьева, 6
Тел. (383 2) 34-33-53
Факс (383 2) 34-37-83
Е-mail: mikh@sscc.ru

Директор — чл.-кор. РАН Михайленко Борис Григорьевич
Заместитель директора по науке — чл.-кор. РАН Михайлов Геннадий Алексеевич

Общая численность института — 374 чел.; научных сотрудников — 175, академик — 1, членов-корреспондентов РАН — 3, докторов наук — 37, кандидатов наук — 95.

Основные научные направления:

— вычислительная математика;
— математическое моделирование и методы прикладной математики в геофизике;
— параллельные и распределенные вычисления.

Лаборатории:

Математического моделирования гидросферы (д.ф.-м.н. В.И. Кузин)
Динамики климата (д.ф.-м.н. А.А. Фоменко)
Математического моделирования гидродинамических процессов в природной среде (д.ф.-м.н. В.В. Пененко)
Методов Монте-Карло (чл.-кор. РАН Г.А. Михайлов)
Оптики дисперсных сред (д.ф.-м.н. Б.А. Каргин)
Стохастических задач математической физики (д.ф-м.н. К.К. Сабельфельд)
Численного анализа стохастических дифференциальных уравнений (д.ф.-м.н. С.С. Артемьев)
Вычислительной физики (д.ф.-м.н. В.П. Ильин)
Математических задач химии (д.ф.-м.н. Ю.М. Лаевский)
Математических задач сейсмологии (акад. А.С. Алексеев)
Вибросейсмических исследований (д.ф.-м.н. Г.М. Цибульчик)
Численного моделирования сейсмических полей (чл.-кор. РАН Б.Г. Михайленко)
Математического моделирования волн цунами (д.ф.-м.н. В.К. Гусяков)
Информационных технологий вычислительной геофизики (д.ф.-м.н. В.А. Цецохо)
Моделирования процессов и систем вибросейсмического мониторинга (д.т.н. Б.М. Глинский)
Цифровых методов обработки геофизической информации (д.т.н. М.С. Хайретдинов)
Обработки изображений (д.т.н. В.П. Пяткин)
Параллельных алгоритмов и структур (к.т.н. С.В. Пискунов)
Синтеза параллельных программ (д.ф.-м.н. В.Э. Малышкин)
Анализа и машинной графики (д.ф.-м.н. А.М. Мацокин)
Системного моделирования (д.ф.-м.н. М.И. Нечепуренко)
Математического моделирования информацион ных сетей (д.ф.-м.н. В.К. Попков)
Прикладных систем (к.т.н. С.В. Бредихин)

Основные научные результаты

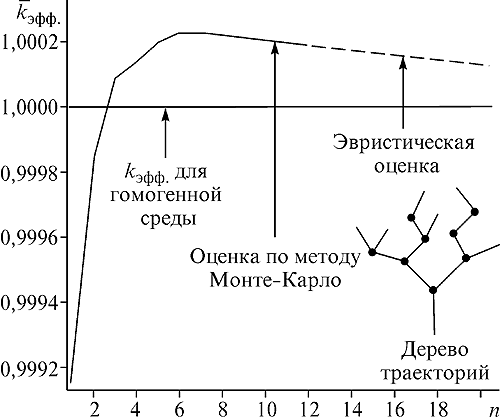
Получены оценки вероятностных моментов критических значений параметров процесса переноса частиц в среде со случайной плотностью (рис.1). Для этого на основе специального итерационного процесса построены новые оценки производных первого и второго порядка от критических параметров по значениям плотности в различных подобластях среды. Кроме реакторных систем, методика применима для исследования временной асимптотики помехи обратного рассеяния.

Рис. 1. Аномальное поведение среднего коэффициента размножения частиц при увеличении числа независимых подобластей случайной среды. Fig. 1. Abnormal behaviour of average factor of duplication of particles at increase of number of independent subareas of the random environment.

Для линейных операторных уравнений первого рода построена теория адаптивной оптимизации двухслойных градиентных итерационных методов с экономичными факторизованными переобуславливателями. Получены новые оценки скорости сходимости, неулучшаемые для данного класса переобуславливателей. Весьма существенно, что в отличие от ранее известных подходов, при вычислении адаптивно оптимальных переобуславливателей не требуется априорная спектральная информация. Значимость полученных результатов определяется возможностью существенного повышения эффективности математического обеспечения для широкого круга практических задач посредством применения высокопроизводительных многопроцессорных комплексов.

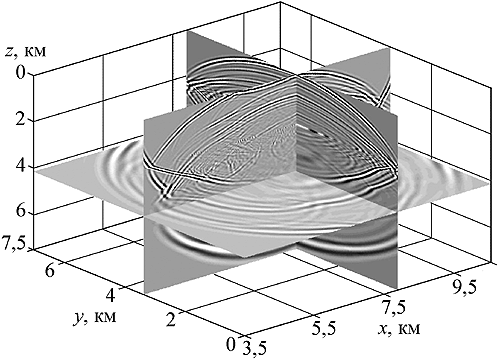
Разработан метод решения динамических задач сейсмики для упругих и вязкоупругих моделей сред большой размерности, адаптированный для многопроцессорных вычислительных систем. Алгоритм основан на комплексировании интегральных преобразований Лагерра по времени с высокоточными разностными методами по пространственным переменным. Метод особенно эффективен при решении динамических задач сейсмики для двумерно и трехмерно неоднородных резкоконтрастных моделей сред большой размерности (рис. 2).

Рис. 2. Пример расчета полного волнового поля в сложной трехмерно-неоднородной упругой среде. Fig. 2. An example of calculation of the full wave field in the complex 3-D inhomogeneous elastic medium.

Построены и численно исследованы новые математические модели процессов распространения гибридных волн фильтрационного горения. Такие процессы относятся к классу процессов с избытком энтальпии, что делает их чрезвычайно перспективными с технологической точки зрения (сжигание низкокалорийных топлив в энергетических и экологических целях). Разработан новый высокоэффективный алгоритм. Определены важные характеристики процесса: скорость движения волны, ширина зоны реакции, максимальные температуры в газе и пористом теле. Получены динамические характеристики выхода на стационарный режим и определена зависимость положения стационарного фронта горения от расхода газа.

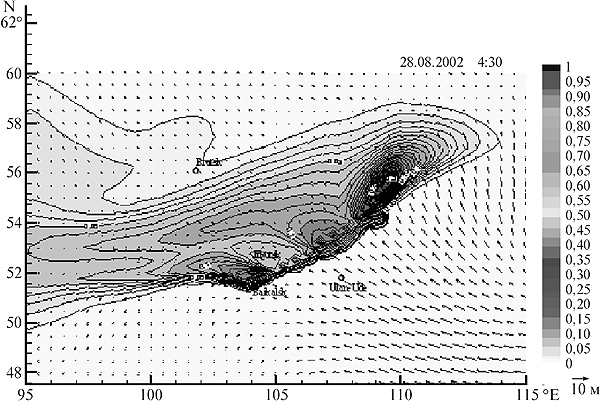
Разработан новый метод оценок экологических рисков и уязвимости территорий относительно антропогенных воздействий с учетом динамики глобальной климатической системы. Он предназначен для выявления предпосылок экологических катастроф и прогнозирования их последствий методами прямого и обратного моделирования на базе моделей гидродинамики и переноса загрязняющих примесей (рис. 3).

Рис. 3. Результат моделирования функции экологического риска для озера Байкал от источников загрязнений, расположенных в регионе. Показаны двумерные сечения поля ветра и поля функции риска на уровне приземного слоя. Fig. 3. Result of the modelling function of ecological risk for lake Baikal from sources of the pollution located in region. 2-D sections of a wind field and a risk function field at a level of a ground layer are shown.

Всего за 2003 г. институтом опубликовано: статей в рецензируемых журналах — 156, монографий — 9.

Создан 17 января 1975 г.
Адрес: 660036 Красноярск, Академгородок
Тел/факс (391 2) 43-27-56
E-mail: sek@icm.krasn.ru

Директор — чл.-кор. РАН Шайдуров Владимир Викторович
Заместители директора по науке:
д.т.н. Москвичев Владимир Викторович
д.т.н. Ноженкова Людмила Федоровна

Общая численность института — 135 чел.; научных сотрудников — 78, член-корреспондент РАН — 1, докторов наук — 24, кандидатов наук — 53.

Основные научные направления:

— методы вычислительной математики и технология математического моделирования для решения задач физики, механики, физической химии;
— интеллектуальные, нейросетевые и геоинформационные технологии, распределенные информационные системы;
— методы математического моделирования и вычислительного эксперимента для обеспечения прочности материалов и конструкций, безопасности сложных систем и объектов.

Отделы:
Дискретной математики (д.ф.-м.н. О.В. Воробьев)
Дифференциальных уравнений механики (д.ф.-м.н. В.К. Андреев)
Вычислительной математики (чл.-кор. РАН В.В. Шайдуров)
Вычислительной физики (д.ф.-м.н. Н.Я. Шапарев)
Моделирования неравновесных систем (д.ф.-м.н. А.Н. Горбань)
Прикладной информатики (д.т.н. Л.Ф. Ноженкова)
Вычислительных моделей в гидрофизике (д.ф.-м.н. В.М. Белолипецкий)
Машиноведения (д.т.н. В.В. Москвичев)
Вычислительной механики деформируемых сред (д.ф.-м.н. В.М. Садовский)
Хозрасчетная лаборатория распределенных информационных систем (И.И. Сапожков)

Основные научные результаты

Для ряда вычислительных фрагментов решения сеточных аналогов задач математической физики при некоторых условиях обнаружено, а затем теоретически обосновано сверхлинейное ускорение вычислений на вычислительных кластерах, т.е. увеличение скорости вычислений на n процессорах более чем в n раз по сравнению с одним процессором, несмотря на дополнительные операции межпроцессорного обмена данными. Причиной сверхлинейного ускорения является увеличение в n раз суммарного объема кэша всех используемых процессоров и, как следствие, более интенсивный обмен данными с кэшем, а не с оперативной памятью, что в несколько раз медленнее. Прямым подтверждени ем этой гипотезы стало отсутствие эффекта сверхлинейного ускорения при отключении кэша у процессоров. Создана и экспериментально подтверждена модель вычислительного процесса с учетом n-кратного увеличения кэша, в явном виде указывающая условия достижения сверхлиней ного ускорения вычислений при различных соотношениях числа процессоров и скоростей вычислений и межпроцессорных обменов.

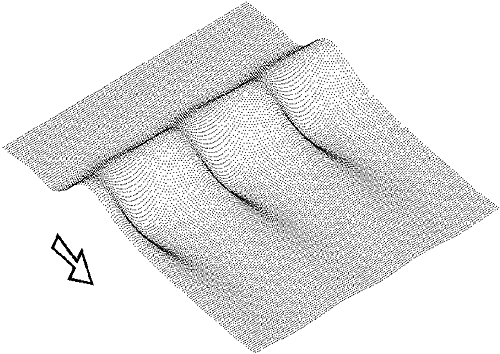
Впервые получено теоретическое описание формирования пространственных регулярных структур (рис. 1) в локально нагреваемой стекающей жидкой пленке, недавно обнаруженных в экспериментах (ИТ СО РАН). Использовался оригинальный метод частиц для несжимаемой жидкости, распространенный на случай вязкой теплопроводной жидкости с переменным поверхностным натяжением. Численное моделирова ние конкретного эксперимента показало хорошее качественное и количественное согласие. В частности, пороговое значение плотности теплового потока, при котором возникает трехмерная неустойчивость, предсказывается расчетами с точностью до 5%. Полученные значения характерной ширины структур согласуются с экспериментом в пределах точности измерений. Расчеты также воспроизводят более тонкие эффекты, такие как увеличение ширины структуры и ее сдвиг вверх по потоку с увеличением нагрева.

Рис. 1. Регулярная структура в стекающей жидкой пленке. Fig. 1. Regular structure in a falling liquid film.

Проведены комплексные исследования работоспособности вертикальных стальных резервуаров для хранения нефтепродуктов объемом 500—20000 м³ с дефектами формы типа «вмятин» (рис. 2). На основе данных технического диагностирования установлены статистические закономерности распределений дефектов формы по геометрическим параметрам. На основе численного анализа методом конечных элементов напряженно-деформированного состояния в линейной, геометрически нелинейной и физически нелинейной постановке выявлены основные закономерности перераспределения напряжений и деформаций в зонах дефектов при нагружении резервуаров. Обнаружен эффект скачкообразного изменения формы вмятин в процессе нагружения резервуара. Получены зависимости для коэффициентов концентрации напряжений в упругой области от относительной глубины и приведенного радиуса дефекта. Что касается области упругопластического деформирования, то при расчетах коэффициентов концентрации напряжений и деформаций в зонах дефектов предложены аналитические соотношения типа уравнений Нейбера—Махутова. Установлено, что для статистически обоснованных размеров дефектов коэффициенты концентрации напряжений варьируются в диапазоне от 2,5 до 12. Расчетные оценки ресурса показали значительные запасы по долговечности эксплуатирующихся резервуаров с дефектами формы. С учетом этого предложена методика нормирования размеров дефектов по условию обеспечения требуемого безопасного остаточного ресурса резервуаров.

Рис. 2. Резервуар РВС 5000 с характерными дефектами формы. Fig. 2. Regular structure with shape defects.

Всего за 2003 г. институтом опубликовано: статья в рецензируемых журналах — 121, монографий —7.

Создан 1 ноября 1980 г.
Адрес: 664033 Иркутск, ул. Лермонтова, 134, а/я 1233
Тел. (3952) 42-71-00
Факс (3952) 51-16-16
E-mail: snv@icc.ru

Директор — чл.- кор. РАН Васильев Станислав Николаевич
Заместители директора по научной работе:
д.ф.-м.н. Лакеев Анатолий Валентинович
к.т.н. Максимкин Николай Николаевич
к.т.н. Ружников Геннадий Михайлович
Директор Улан-Удэнского филиала — д.ф.-м.н. Батурин Владимир Александрович

Общая численность института — 172 чел.; научных сотрудников — 68, член-корреспондент РАН — 1, докторов наук — 18, кандидатов наук — 39.

Основные научные направления:
— научные основы теории и методов управления;
— математические методы и информационные технологии исследования динамических систем.

Научные подразделения:
Отделение теории управления (к.ф.-м.н. Р.И. Козлов)
Лаборатории:
Теории сложных управляемых систем (к.ф.-м.н. Р.И. Козлов)
Теории логико-динамических моделей (д.ф.-м.н. А.В.Лакеев)
Системного анализа и методов оптимального управления (д.ф.-м.н. В.А. Батурин)
Алгебро-дифференциальных систем (д.ф.-м.н. В.Ф. Чистяков)
Методов глобальной оптимизации (д.ф.-м.н. А.С. Стрекаловский)
Отделение математической теории динамических систем (к.ф.-м.н. Г.А. Рудых)
Лаборатории:
Динамики нелинейных систем с распределенными параметрами (к.ф.-м.н. Г.А. Рудых)
Дифференциальных включений и оптимизации (д.ф.-м.н. А.А.Толстоногов)
Устойчивости движения (д.ф.-м.н. В.Д. Иртегов)
Отделение логических методов автоматизации решения задач (д.т.н. Г.А.Опарин)
Лаборатории:
Методов автоматизации исследований управляемых систем (д.т.н. Г.А.Опарин)
Научно-методических и технологических основ информатизации (д.т.н. А.Ф. Берман)
Прикладной математической логики (д.ф.-м.н. В.И. Мартьянов)
Отделение информационных и телекоммуникационных систем (д.т.н. И.В. Бычков)
Лаборатории:
Методов и систем искусственного интеллекта (д.т.н. И.В. Бычков)
Методов представления и обработки информации (к.т.н. А.Е. Хмельнов)
Телекоммуникационных и вычислительных систем (к.ф.-м.н. С.В. Бурносов)
Филиал ИДСТУ (Улан-Удэ) (д.ф.-м.н. В.А. Батурин)

Основные научные результаты

Для систем с широтно-импульсным управлением на основе метода векторных функций Ляпунова (ВФЛ) получены конструктивные условия диссипативности, явно выраженные через параметры системы. Разработаны алгоритмы вычисления строгих количественных оценок предельного множества, области притяжения и времени достижения требуемого уровня точности, доведенные до формул, применимых в инженерной практике, и в отличие от мирового уровня учитывающие нелинейности и погрешности измерителей, исполнительных органов, модуляционной характеристики, формы импульсов и неопределенности внешних воздействий. При решении задачи применено двухэтапное использование ВФЛ (разные ВФЛ для больших и малых отклонений) и непосредственное построение дискретной системы сравнения, минуя дискретизацию исходной модели, что позволило получить более точные оценки качества. Выполнены приложения к исследованию режимов реактивного успокоения космических аппаратов (типа спутников связи), особенностями которых являются значительное влияние упругости конструкции, наличие низких собственных частот с малыми декрементами и сравнительно большое запаздывание в формировании импульсов. Благодаря использованию математической модели, описывающей реальные системы более точно по сравнению с известными, показана возможность гарантированной точности успокоения (рис. 1).

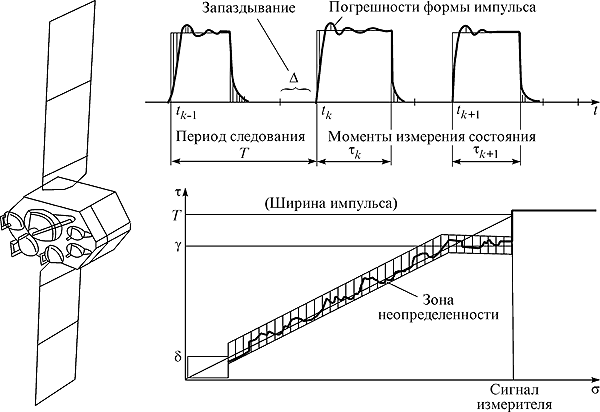Рис. 1. Режим успокоения космических летательных аппаратов класса спутников связи. Fig. 1. The mode of quite of spacecraft of the class of communication satellites.

В сепарабельном гильбертовом пространстве исследованы включения с многозначным возмущением и эволюционными операторами, являющимися субдифференциалами зависящей от времени собственной выпуклой полунепрерывной снизу функции. Наряду с исходным включением рассматривается последовательность аппроксимирующих включений с тем же возмущением и эволюционными операторами, являющимися субдифференциалами регуляризаций Моро—Иосиды исходной функции. Показано, что множество достижимости исходного включения является равномерным по времени пределом в метрике Хаусдорфа последовательности множеств достижимости аппроксимиру ющих включений. В качестве приложений полученных результатов рассмотрены примеры управляемых систем с разрывными нелинейностями. Для таких систем найдены аппроксими рующие последовательности гладких управляемых систем, для которых проведено численное построение множеств достижимости (рис. 2). Результат, касающийся аппроксимации множеств достижимости включений и управляемых систем данного типа, не имеет аналогов в мире.

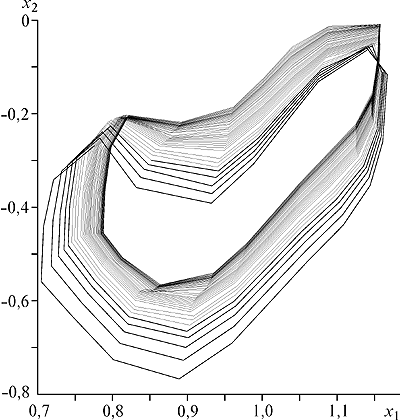Рис. 2. Результаты расчетов показывают быструю сходимость множеств достижимости аппроксимирующих управляемых систем к множеству достижимости управляемой системы с разрывными нелинейностями. Fig. 2. Results of simulation shows quick convergence of reachable sets which approximate of control systems to the reachable set of control system with break nonlinearity.

Для задач, возникающих при математическом моделировании диффузии ограниченной плазмы через магнитное поле, методами нелинейного анализа доказана разрешимость краевой задачи Дирихле для равномерно эллиптической системы с нелокальными нелинейностями. Получены достаточные условия существования и единственности классического стационарного решения, построена его область притяжения. Для нелинейных параболических уравнений теплопроводности с неявным вырождением доказано существование новых точных, анизотропных по пространственным переменным, явных решений в замкнутом виде. Показана инвариантность уравнения быстрой диффузии в двумерном координатном пространстве и проведена его редукция к одномерному по пространственной переменной аналогу, построены новые точные решения уравнения (рис. 3). В отличие от известных результатов, предложенный подход позволяет свести построение нижних и верхних решений к конечномерным задачам и тем самым определить эти решения в явном виде.

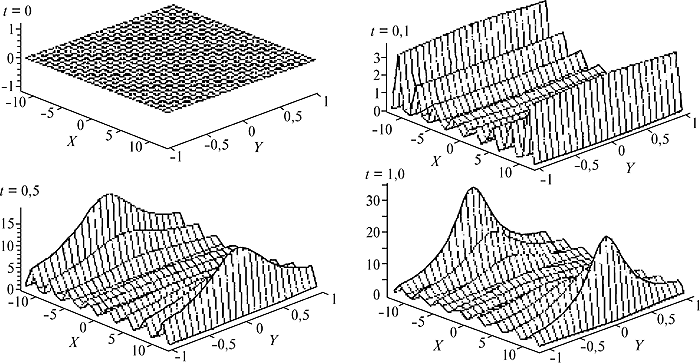Рис. 3. Графики решения уравнения быстрой диффузии в различные моменты времени. Fig. 3. Graphics of solution of quick diffusion equation in the different time moments.

Всего за 2003 г. институтом опубликовано: статей в рецензируемых журналах — 62, монографий — 3.

Создан 25 мая 1990 г.
Адрес: 630090 Новосибирск, просп. Академика М.А. Лаврентьева, 6
Тел. (383 2) 34-11-50
Факс (383 2) 34-13-42
Е-mail: ict@ict.nsc.ru

Директор — акад. Шокин Юрий Иванович
Заместители директора по науке:
чл.-кор. РАН Федотов Анатолий Михайлович
д.ф.-м.н. Ковеня Виктор Михайлович

Общая численность института — 97 чел.; научных сотрудников — 55, академик — 1, член-корреспондент РАН — 1, докторов наук — 14, кандидатов наук — 30.

Основные научные направления:
— разработка информационно-телекоммуникационных технологий в задачах принятия решений;
— математическое моделирование и вычислительные технологии в области механики сплошной среды, физики и экологии.

Лаборатории:
Прикладной математики (акад. Ю.И. Шокин)
Вычислительной аэрогидродинамики (д.ф.-м.н. В.М. Ковеня)
Вычислительной физики (д.ф.-м.н. М.П. Федорук)
Информационных технологий (чл.-кор. РАН А.М. Федотов)
Защиты информации в телекоммуникационных системах (к.т.н. В.С. Никульцев)
Информационных ресурсов (к.ф.-м.н. С.К. Голушко)
Центр информационно-технического обеспечения (В.С. Стогниенко)

Основные научные результаты

Предложен новый класс статистических критериев, эффективность которых при тестирова нии генераторов случайных чисел в сотни раз выше, чем у лучших известных алгоритмов, включая алгоритмы, рекомендованные Национальным институтом стандартов и технологий (США) для использования в криптографических системах защиты информации.

Построена квазилинейная теория нелинейного уравнения Шредингера (НУШ) с периодическими коэффициентами в условиях большой вариации локальной дисперсии. Решение после n периодов представляется в виде суммы решения линейной части НУШ и нелинейной поправки на первом периоде, умноженной на число периодов n. Получено явное выражение нелинейной поправки к решению для последовательности импульсов гауссовской формы. Предложен численный алгоритм вычисления квазилинейного решения в случае произвольных начальных условий. Результаты расчетов показывают, что квазилинейное приближение достаточно хорошо описывает эволюцию сигнала и может быть использовано для численного моделирования периодических волоконно-оптических линий передачи.

Для численного анализа динамики свободной турбулентности в линейно стратифицированной среде построены численные модели, основанные на применении иерархии современных полуэмпирических моделей турбулентности и метода расщепления по пространственным переменным. Модели тестировались на задаче об эволюции турбулентного следа за самодвижущимся телом в линейно стратифицированной жидкости. Показано, что удовлетворительное описание процесса анизотропного вырождения турбулентности достигается с применением моделей, включающих усовершенствованные аппроксимации тройных корреляций поля скорости, более детально учитывающих воздействие силы тяжести и модифицированное уравнение переноса скорости диссипации (рис. 1).

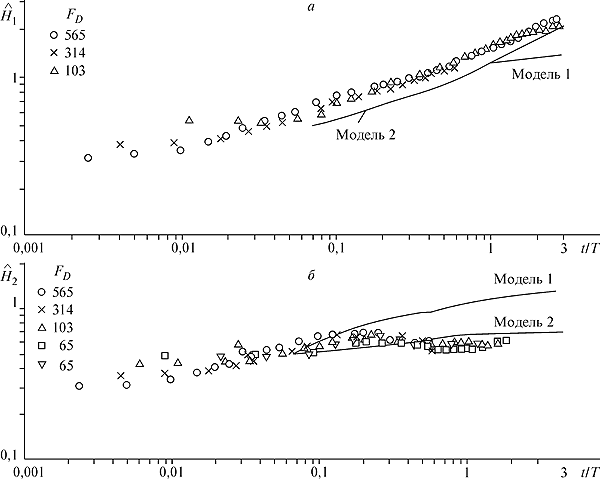Рис. 1. Изменение во времени горизонтального (а) и вертикального (б) размеров турбулентного следа. Точки — экспериментальные данные [Lin and Pao, 1979]; линии — расчеты; FD=U0T/D  — плотностное число Фруда, U0 — скорость движения тела, D — диаметр тела, T — период Вяйсяля-Брента. Fig. 1. Time variation of the wake width (а) and wake height (б). Points-experimental data [Lin and Pao, 1979]; lines — calculations; FD=U0T/D — density Froude number, U0 — velocity of the moving body, D — body diameter, T  — the Vaisala-Brunt period.

На основе метода частиц в ячейках разработан эффективный параллельный алгоритм решения задач динамики взаимодействия сверхмощных лазерных импульсов с плазмой до- и сверхкритической плотности. Система уравнений, описывающая динамику ускорения частиц и эволюцию электромагнитного поля, состоит из кинетического уравнения Власова для функции распределения частиц по скоростям и уравнений Максвелла. В результате серии вычислительных экспериментов получены зависимости энергии ускоренных электронов от плотности плазмы и интенсивности лазерного излучения, исследован механизм ускорения ионов в постсолитонной плазме (рис. 2).

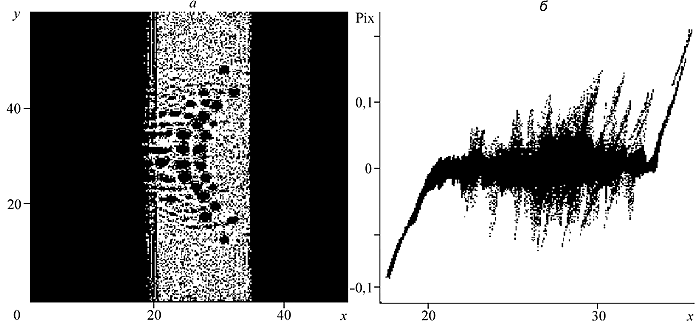Рис. 2. Постсолитонная структура плотности ионной компоненты плазмы, сформированная в результате прохождения лазерного импульса (а). Фазовая плоскость ионов (Pix — x), демонстрирующая ускорение ионов в постсолитонной плазме (б). Fig. 2. Post-soliton structure of plasma ion density generated by laser pulse (а). Phase plane (Pix— x): ion acceleration in post-soliton plasma (б).

Всего за 2003 г. институтом опубликовано: статей в рецензируемых журналах — 122, монографий — 2.

Cоздан 30 марта 1990 г.
Адрес: 630090 Новосибирск, просп. Академика М.А. Лаврентьева, 6
Тел. (383 2) 34-36-52
Факс (383 2) 32-34-94
E-mail: mag@iis.nsk.su

Директор — д.ф.-м.н. Марчук Александр Гурьевич
Заместитель директора по науке — д.ф.-м.н. Яхно Татьяна Михайловна

Общая численность института — 148 чел.; научных сотрудников — 75, член-корреспондент РАН — 1, докторов наук — 7, кандидатов наук — 33.

Основное научное направление:
— исследования в области теоретических и методологических основ информатики, включая теоретические основания информатики; методы и инструменты построения программ повышенной надежности и эффективности; методы и системы искусственного интеллекта; системное и прикладное программное обеспечение перспективных вычислительных машин, систем, сетей и комплексов.

Лаборатории:
Теоретического программирования (к.ф.-м.н. В.А. Непомнящий)
Автоматизации проектирования и архитектуры СБИС (д.ф.-м.н. А.Г. Марчук)
Системного программирования (к.т.н. В.И. Шелехов)
Искусственного интеллекта (к.т.н. Ю.А. Загорулько)
Смешанных вычислений (к.ф.-м.н. М.А. Бульонков)
Конструирования и оптимизации программ (д.ф.-м.н. В.Н. Касьянов)
Научно-исследовательские группы:
Переносимых систем программирования (А.Д. Хапугин)
Моделирования сложных систем (к.ф.-м.н. А.Л. Семенов)

Основные научные результаты

Предложен полиномиальный по сложности алгоритм нижней и верхней аппроксимаций проверки моделей для базовой логики действий с неподвижными точками — μ-исчисления. Изучена проблема проверки моделей для взаимодействующих распределенных агентов в терминах комбинированных логик знаний и действий с конструкциями для неподвижных точек. Реализован экспериментальный программный комплекс SPV (SDL Protocol Verifier), предназначенный для моделирования и верификации коммуникационных протоколов, включающий верификатор раскрашенных сетей Петри, который использует метод проверки моделей относительно свойств, представленных в μ-исчислении (рис. 1). Этот же метод реализован в системе верификации выполнимых спецификаций, представленных на языке Basic-REAL.

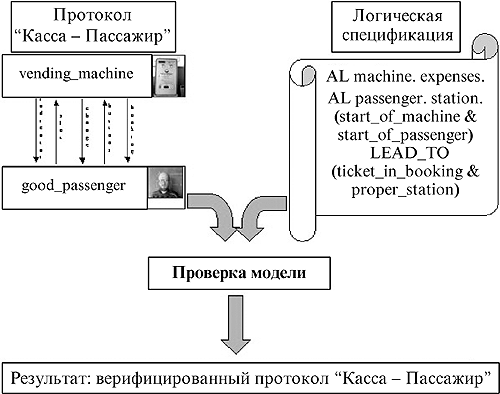Рис. 1. Схема верификации протокола. Fig. 1. Protocol Verification Scheme.

Создана технология построения кооперативных решателей, использующих различные вычислительные методы. Реализован широкий набор методов, включающий методы интервальной математики, решения оптимизационных задач и современные методы искусственного интеллекта (рис. 2). Разработан язык для интегрирования методов, описания архитектуры решателей, способов параллельного и распределенного взаимодействия методов. Данная технология соответствует мировому уровню работ в этой области, а в некоторых аспектах превосходит их. Проведенные эксперименты показали высокую эффективность разработанного подхода.

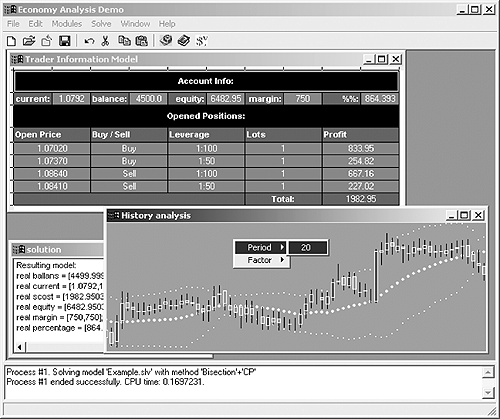Рис. 2. Пример: анализ процессов на рынке. Fig. 2. Example: analysis of processes on the market.

Разработан и реализован ряд оригинальных алгоритмов для обработки сигналов, возникающих при ядерном каротаже нефтяных скважин. Создан программный комплекс «Анализатор спектров» (рис. 3), предоставляющий широкие возможности: загрузка, просмотр и обработка исходных экспериментальных амплитудных и временных спектров; расчет ряда аналитических параметров; вычисление концентраций естественных радионуклидов; экспорт результатов обработки в формате LAS, применяемом в геофизике. Алгоритмы и программный комплекс используются при эксплуатации нефтяных месторождений и конкурентоспособны с мировыми аналогами.

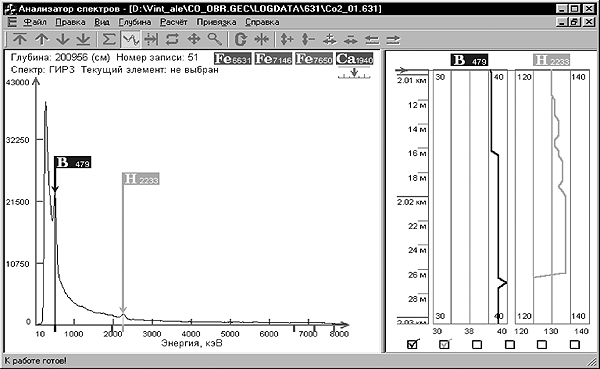Рис. 3. Главное окно программы «Анализатор спектров». Fig. 3. The main window of the program «Spectrum Analyzer».

Всего за 2003 г. институтом опубликовано: статей в рецензируемых журналах — 16, монографий — 2.

Создан 6 октября 1981 г.
Адрес: 630090 Новосибирск, ул. Институтская, 6
Тел. (383 2) 34-43-61, 34-43-43
Факс (383 2) 34-43-61
E-mail: beht@kti.nsc.ru

Директор Института — к.т.н. Собстель Геннадий Михайлович
Заместители директора по науке:
к.т.н. Зензин Александр Степанович
к.т.н. Золотухин Евгений Павлович

Общая численность института — 164 чел.; научных сотрудников — 35; доктор наук — 1, кандидатов наук — 16.

Лаборатории:
Информационных систем (к.т.н. Б.Н. Пищик)
Индустриальной информатики (к.т.н. Г.П. Чейдо)
Систем автоматизации для научных исследова ний и промышленных применений (И.В. Меркулов)
Биомедицинской информатики (д.б.н. А.С. Ратушняк)
Автоматизированных систем (к.т.н. Э.Г. Михальцов)
Вычислительных систем и сетей (В.Н. Окунишников)
Измерительных систем и приборостроения (В.В. Гаркуша)
Биоинформатики (Ф.А. Колпаков)
Оптоэлектроники (к.х.н. В.Г. Гаранин);
Сектор цифровых управляющих систем (В.Д. Нескородев)

Основные научные результаты

Завершен цикл работ, связанный с разработкой, проектированием и созданием программно-технического комплекса (ПТК) Автоматизированной системы управления технологическими процессами Северо-Муйского тоннеля (АСУ ТП СМТ).

Северо-Муйский тоннель — это уникальный, сложный технический объект, большой протяженности и энергонасыщенности. Его протяженность составляет 15343 м (6 место в мире), общая длина подземных выработок превышает 35 км. Тоннель расположен в зоне резко континентального климата со среднегодовой температурой –6,7°С. По сейсмогеологическим данным, сейсмическая опасность района Северо-Муйского тоннеля превышает 9 баллов.

АСУ ТП СМТ предназначена для автоматизации управления технологическими процессами в СМТ и обеспечивает:

— сбор информации о параметрах воздушной среды внутри и снаружи тоннеля, температуре обделки и воды в водоотводных устройствах, состоянии технологического оборудования тоннеля и концентрации вредных газов в атмосфере тоннеля;

—формирование и передачу сигналов управления технологическим оборудованием тоннеля с автоматизированного рабочего места (АРМ) диспетчера в ручном и автоматическом режимах (рис. 1.);

— оперативное отображение состояния технологического оборудования тоннеля и параметров микроклимата тоннеля на мониторе АРМ диспетчера;

— обработку и архивирование собранной информации;

— протоколирование действий диспетчера и состояния технологического оборудования.

Рис. 1. Фрагмент схемы тоннеля (а) и станция оперативного управления (б). Fig. 1. Segment of a tunnel scheme (а) and on-line control station (б).

Всего за 2003 г. институтом опубликовано: статей в рецензируемых журналах — 4.

Cоздан 18 мая 1957 г.
Адрес: 630090 Новосибирск, просп. Академика В.А. Коптюга, 4
Тел. (383 2) 33-28-92,
Факс (383 2) 33-25-98
E-mail: im@math.nsc.ru

Директор — акад. Ершов Юрий Леонидович
Заместители директора по науке:
д.ф.-м.н. Береснев Владимир Леонидович
д.ф.-м.н. Фокин Михаил Валентинович
д.ф.-м.н. Топчий Валентин Алексеевич

Общая численность института — 533 чел.; научных сотрудников — 357, академиков — 5, членов-корреспондентов РАН — 4, докторов наук — 109, кандидатов наук — 218.

Основные научные направления:
— алгебра, теория чисел и математическая логика;
— геометрия и топология;
— математический анализ, дифференциальные уравнения и математическая физика;
— теория вероятностей и математическая статистика;
— вычислительная математика;
— математическое моделирование и методы прикладной математики.

Лаборатории:
Условно-корректных задач (д.ф.-м.н. Д.С. Аниконов)
Волновых процессов (чл.-кор. РАН В.Г. Романов)
Обратных задач математической физики (д.ф.-м.н. Ю.Е. Аниконов)
Численных методов решения обратных задач (д.ф.-м.н. А.Л.Бухгейм)
Теории функций (д.ф.-м.н. В.В. Асеев)
Дифференциальных уравнений математической физики (д.ф.-м.н. Е.И. Роменский)
Вычислительных проблем задач математической физики (д.ф.-м.н. А.М. Блохин)
Дифференциальных уравнений и смежных вопросов анализа (д.ф.-м.н. В.С. Белоносов)
Динамических систем (чл.-кор. РАН И.А. Тайманов)
Геометрии и теории функций вещественных переменных (акад. Ю.Г. Решетняк)
Функционального анализа (д.ф.-м.н. С.С. Кутателадзе)
Топологии и хроногеометрии (д.ф.-м.н. В.И. Кузьминов)
Прикладного анализа (д.ф.-м.н. В.В. Вершинин)
Неассоциативных колец (д.ф.-м.н. В.Н. Желябин)
Алгебраических систем (д.ф.-м.н. Е.А. Палютин)
Теории групп (чл.-кор. В.Д. Мазуров)
Математической логики (д.ф.-м.н. А.С. Морозов)
Теории вычислимости и прикладной логики (чл.-кор. РАН С.С. Гончаров)
Исследования операций (д.ф.-м.н. В.Т. Дементьев)
Численных методов оптимальных процессов (к.т.н. В.М. Александров)
Дискретного анализа (к.ф.-м.н. А.А. Евдокимов)
Дискретных экстремальных задач (к.ф.-м.н. Н.И. Глебов)
Математических моделей принятия решений (д.ф.-м.н. В.Л. Береснев)
Теории графов (д.ф.-м.н. О.В. Бородин)
Методов оптимизации (д.ф.-м.н. В.И. Шмырев)
Математической экономики (д.ф.-м.н. В.А. Васильев)
Анализа данных (д.т.н. Г.С. Лбов)
Теории сплайн-функций (к.ф.-м.н. В.Л. Мирошниченко)
Численных методов исследования моделей (д.ф.-м.н. С.И. Фадеев)
Логических основ программирования (д.ф.-м.н. Д.Е. Пальчунов)
Омский филиал Института (д.ф.-м.н. В.А. Топчий)

Основные научные результаты

Алгебра, теория чисел и математическая логика. Полностью описаны все возможные семейства Σ-подмножеств множества натуральных чисел в допустимых множествах. Получена новая серия примеров допустимых множеств без универсальной Σ-функции.

Доказано, что существует лишь конечное число позитивных пропозициональных логик с проективным свойством Бета, и найдено их исчерпывающее описание.

На основе обобщения теоремы о ветвящихся моделях и новых алгебраических инвариантах получено полное описание автоустойчивых булевых алгебр с выделенными идеалами и спектра их алгоритмических размерностей.

Установлена определимость класса o-минимальных и слабо o-минимальных теорий через E^*-стабильность.

Доказано, что алгебра Ли с автоморфизмом конечного порядка, имеющим конечномерную подалгебру неподвижных точек, обладает разрешимым идеалом конечной коразмерности.

Показано, что произвольная супералгебра Шура квазинаследственна или клеточна тогда и только тогда, когда она полупроста.

Геометрия и топология. Исследованы квазиизометрические отображения областей в многомерных евклидовых пространствах. Установлено, что с точностью до изометрии пространства отображение зависит непрерывно в смысле топологии классов Соболева от своего метрического тензора.

Математический анализ, дифференциальные уравнения и математическая физика. Получено описание отображений, индуцирующих по правилу суперпозиции ограниченный оператор (или изоморфизм) пространств Соболева с первыми обобщенными производными.

Доказано, что если r > 1 и система l-го порядка линейных дифференциальных уравнений в частных производных с измеримыми коэффициентами и правыми частями является равномерно эллиптической, то при достаточно медленном изменении старших ее коэффициентов степень локальной суммируемости старших производных каждого W¹_r.loc-решения системы такая же, как у ее младших коэффициентов и правых частей.

Для произвольного интегрального функционала доказана плотность множества функций, на которых он одновременно устойчив и полунепрерывен снизу.

Разработана термодинамически согласован ная модель нелинейной упругости, описываемая симметрической гиперболической системой. При таком моделировании используется лишь часть решений, подчиненных дополнительным уравнениям, совместным с системой. Только на этих решениях справедливы законы сохранения, которые обычно рассматриваются в виде уравнений, управляющих упругими процессами.

Вычислены относительные интенсивности распадов и кривые возбуждения векторных резонансов в пятипионных каналах. Предложены способы проверки теоретических предсказаний. Обосновано новое направление — исследование киральной динамики многопионных систем.

Теория вероятностей и математическая статистика. Найдена асимптотика вероятностей больших уклонений распределения вещественнозначной асимптотически однородной цепи Маркова в так называемом крамеровском случае, когда скачки цепи имеют конечные экспоненциальные моменты. Для таких цепей установлена временная зона, в которой хвост распределения эквивалентен хвосту инвариантного распределения.

Для критического ветвящегося процесса Гальтона—Ватсона получено обобщение классической теоремы Крамера о вероятностях больших уклонений. Найдены верхние оценки для вероятностей больших уклонений как в случае выполнения условия Крамера, так и в случае, когда существует лишь конечное число моментов выше первого.

Вычислительная математика. На основе обобщения метода Гельфанда—Левитана—Крейна построен алгоритм численного решения многомерной обратной задачи акустики об определении плотности среды.

Математическое моделирование, методы вычислительной и прикладной математики и их применение. Доказано, что всякая центрированная функция (сумма значений в каждом шаре радиуса 1 равна нулю), заданная на дискретном пространстве с метрикой Хэмминга, состоящем из всех вершин n-мерного единичного куба, может быть восстановлена внутри произвольной сферы по ее значениям на этой сфере.

Для широкого класса задач теории расписаний, в которых допускается прерывание операций, получен ряд общих результатов, касающихся существования и структурных свойств оптимальных решений. Доказана теорема о структуре оптимального решения задач в случае целевых функций вида суммы или максимума конечного числа кусочно-линейных функций, зависящих от моментов завершения операций. Установлены полиномиальные верхние оценки на число прерываний в оптимальном расписании.

Получена верхняя оценка аддитивной сложности слова, зависящая только от кратностей вхождения подслов фиксированной длины и достижимая на наиболее сложных словах.

Разработаны точные и приближенные алгоритмы с гарантированными оценками точности для задачи двухуровневого программирования с ограничениями общего вида на верхнем уровне и с задачей о многовариантном ранце на нижнем уровне.

Для задачи календарного планирования с ограниченными ресурсами разработан новый алгоритм локального поиска, основанный на идее чередующихся окрестностей.

Охарактеризованы равномерно рекуррентные бесконечные слова, имеющие линейно растущую арифметическую сложность.

Дано полное описание фасет многогранника Вебера. Предложен новый подход к сравнительному анализу взвешенных дележей Шепли и вероятностных значений кооперативных игр, основанный на полученной характеризации d-распределений Вебера.

Найдены оценки качества получаемых решений для эволюционных методов типа алгоритма случайного поиска с пересчетом при неудачном шаге, а также условия, при которых эти методы оказываются наилучшими в классе эволюционных алгоритмов.

Предложено формальное описание синтаксиса языка машин состояний UML и его операционной семантики. Определено подмножество этого языка, допускающее эффективное построение. Разработан и реализован алгоритм трансляции спецификаций UML в исполняемый код на языке Java.

Всего за 2003 г. институтом опубликовано: статей в рецензируемых журналах — 324, монографий — 23.

Создан 5 июля 2001 г.
Адрес: 634021 Томск, просп. Академический, 2
Тел. 49-13-16, 49-24-33
Факс 49-24-33
E-mail: opi@hq.tsc.ru

И.о. директора — д.т.н., профессор Сырямкин Владимир Иванович

Общая численность отдела — 9 чел.; штатных — 4 чел., совместителей — 5 чел.; научных сотрудников — 7, докторов наук — 4, кандидатов наук — 3.

Основное научное направление:
— синтез и анализ информационных систем моделирования, проектирования, управления.

Основные научные результаты

Разработана информационно-телекоммуникационная система оперативного назначения, в основу проектных решений которой заложены четыре основных принципа построения распределенной территориальной системы оповещения и связи: централизованное управление, интеграция различных каналов связи, единое информационное поле, пакетная передача информации, позволяющая передавать информацию по КВ и УКВ радиоканалам, телефонным и телеграфным линиям, через абонентские терминалы спутниковых систем связи. Интеграция каналов связи позволяет значительно повысить уровень надежности и гибкости системы в целом, а также ввести новое понятие — «динамический ресурс связи».

Разработан принцип построения и реализован оптико-телевизионный измерительный комплекс для задач анализа и аттестации структуры конструкционных и композиционных материалов, исследований процессов пластической деформации и разрушения, а также неразруша ющего контроля состояния нагруженных деталей машин и элементов конструкций.

Всего за 2003 г. отделом опубликовано: статей в рецензируемых журналах — 18.

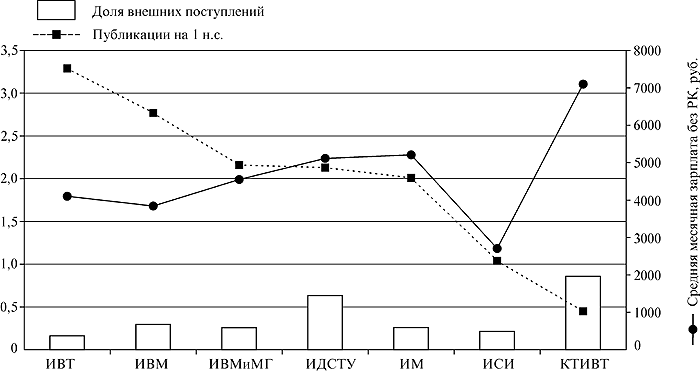
Показатели эффективности деятельности институтов в 2003 году
(математика, информатика)

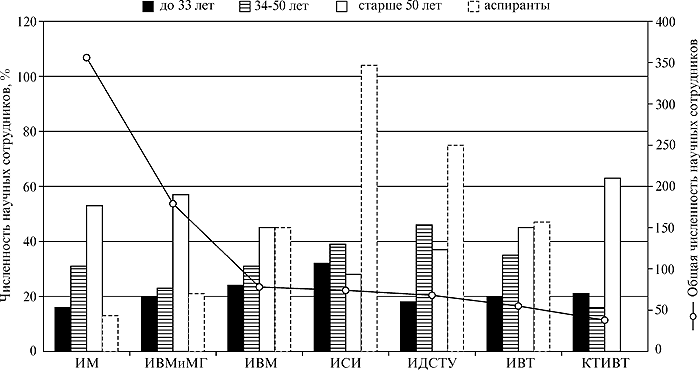
Возрастной состав научных сотрудников институтов
(математика, информатика)

---

В оглавление

Далее

---

Ваши комментарии Обратная связь

[СО РАН] [ИВТ СО РАН]

© 1996-2014, Сибирское отделение Российской академии наук, Новосибирск
© 1996-2014, Институт вычислительных технологий СО РАН, Новосибирск
    Дата последней модификации: Wednesday, 19-Jan-2005 13:44:57 NOVT