ВИЗУАЛИЗАЦИЯ ТРЕХМЕРНЫХ ПРОФИЛЕЙ СКОРОСТЕЙ ПОТОКОВ ГАЗОВ
И ЖИДКОСТЕЙ ПРИ МАССОПЕРЕНОСЕ В ПОРИСТЫХ СРЕДАХ И ОБЪЕКТАХ
СЛОЖНОЙ ГЕОМЕТРИИ С ПОМОЩЬЮ ЯМР-ТОМОГРАФИИ И
ИСПОЛЬЗОВАНИЕ ЭТОЙ ВИЗУАЛИЗАЦИИ ДЛЯ РАЗРАБОТКИ СОВРЕМЕННЫХ
ТЕХНОЛОГИЧЕСКИХ ПРОЦЕССОВ
Координаторы: акад. Пармон В. Н., член-корр. РАН Фомин В. М.
Исполнители: МТЦ, ИК, ИХКГ, ИТПМ, ИХТТМ СО РАН
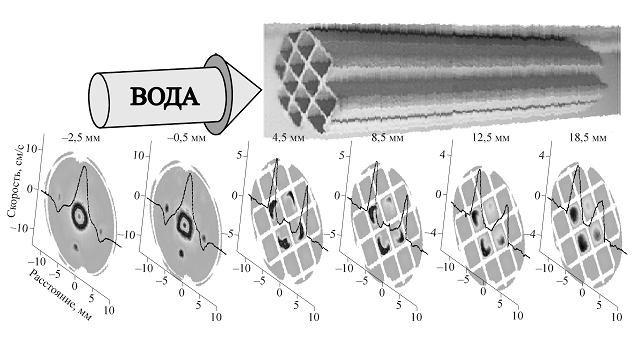
Впервые в отечественной практике методом ЯМР-томографии изучены процессы массопереноса газовой, жидкой и дисперсной твердой фаз через объекты сложной геометрии, включая организованные блочные структуры (рис. 1) и засыпки гранул произвольной формы. Визуализированы процессы массопереноса и образование застойных зон, а также зарегистрирована дисперсия скоростей потока при фильтрации через гранулированный слой.
 |
|
Рис. 1. Двумерные карты распределения скоростей течения воды в цилиндрической кювете с блочным катализатором и их центральные одномерные сечения.
Показана компонента скорости, направленная вдоль каналов блока. Двумерные сечения зарегистрированы на разных расстояниях от входного торца блока, отрицательные расстояния соответствуют сечениям вне блока.
Fig. 1. Two-dimensional maps of the spatial velocity distributions for water flowing in a cylindrical cell with a monolith, and their central one-dimensional cross-sections.
The velocity component along the monolith channels is shown. The two-dimensional maps are detected at various distances from the inlet edge of the monolith, with the negative distances corresponding to the cross sections located outside the monolith.
|
Показано, что изменение пористой структуры слоя сорбента типа “соль в пористой матрице” при варьировании количества связующего, а также размера исходных частиц сорбента может приводить к переходу между крайними режимами сорбции, лимитируемыми диффузией воды либо в слое, либо в исходных частицах. В результате оптимизации пористой структуры слоя на основе оксида алюминия достигнуто увеличение массопереноса без ухудшения переноса тепла. Из данных по распределению сорбированной воды в слое (рис. 2), а также изменению температуры слоя в процессе сорбции найдены значения эффективных коэффициентов диффузии воды. Определены величины теплопроводности слоя сорбента в зависимости от количества сорбированной воды. Исследованные сорбенты, такие как хлорид кальция в силикагеле или оксиде алюминия, являются перспективными для применения в тепловых насосах. Работа важна для создания системного подхода к синтезу сорбентов с контролируемой пористой структурой.
 |
Рис. 2. Распределение сорбированной воды в слое композитного сорбента на основе оксида алюминия.
Время сорбции 10 мин 50 с (1), 1 ч 37 мин (2), 3 ч 3 мин (3), 4 ч 29 мин (4), 7 ч 21 мин (5), 10 ч 13 мин (6). а - фракция исходных частиц 250-500 мкм, 20 % связующего, б - 250-500 мкм, 10 % связующего, в - 250-500 мкм, 2,5 % связующего.
Fig. 2. Spatial distribution of the adsorbed water in a layer of the alumina-based composite sorbent.
Adsorption time: 10 min 50 s (1), 1 hour 37 min (2), 3 hours 3 min (3), 4 hours 29 min (4), 7 hours 21 min (5), 10 hours 13 min (6). a - Primary particles size 250 - 500 mm, with 20 % binder; б - 250-500 mm, with 10 % binder; в - 250-500 mm, with 2.5 % binder.
|
С целью выяснения физического механизма и построения целостной математической модели явлений переноса и экстракции влаги при сушке материалов воздухом комнатной температуры в акустическом поле высокой интенсивности разработана математическая модель, основанная на одномерных линеаризованных уравнениях механики гетерогенных сред с различными скоростями и давлениями компонентов. На основе допущений теории фильтрации в изучаемой математической модели получена асимптотическая фильтрационная модель и дано аналитическое решение задачи о движении жидкости в образце древесины под действием акустических возмущений. Получены интегральные количественные данные о кинетике сушки, продемонстрирован тензорный характер влагопроводности в деревянном образце и определено конкретное значение влагопроводности по направлению перпендикуляра к плоскости поперечного среза дерева (вдоль волокон) в плоском образце. Выполнена экспериментальная визуализация картины осушаемого поля на прозрачных модельных образцах при конвективном и акустическом воздействии (рис. 3). Показано, что начальная стадия процесса акустической сушки может быть адекватно описана с помощью разработанной модели механики гетерогенных сред.
 |
Рис. 3. Визуализация распределения влаги в модельном объекте в процессе конвективной (слева) и акустической (справа) сушки с интервалом 20 с (сверху вниз).
Fig. 3. Visualization of the distribution of water in a model object during the convective (left) and acoustic (right) drying carried out for 20 s gap (up to bottom).
|
Разработаны эффективные алгоритмы для моделирования упаковок частиц с различными распределениями пор по размерам с возможностью учета пористости различных масштабов, а также карты порового пространства. На основе этого проведены расчеты пространственного распределения потоков флюида в моделях с различной структурой пор (рис. 4). Разработан подход для количественного учета влияния стенок зернистого слоя на упаковку частиц и распределение потоков.
 |
Рис. 4. Модель пористой среды с бидисперсной структурой пор (сверху) и рассчитанные карты структуры потоков различной интенсивности.
Fig. 4. Model of a porous medium with a bi-disperse porous structure (top) and the calculated maps of the flows of various intensity.
|
Список основных публикаций
- Voloshin V. P., Beaufils S., Medvedev N.N. Void space analysis of the structure of liquids. Journal of Molecular Liquids, v. 96—97, 2002, p. 101—112.
- Luchnikov V. A., Gavrilova M. L., Medvedev N. N., Voloshin V. P. The Voronoi-Delaunay Approach for Free Volume Analysis of a Packing of Balls in a Cylindrical Container, The Future Generation Computer Systems, Special Issue on Computer Modeling, Algorithms and Supporting Environments, v. 18, 2002, p. 673—679, Elsevier.
- Коптюг И. В., Ильина Л. Ю., Фенелонов В. Б., Деревянкин А. Ю., Сагдеев Р. З., Пармон В. Н. Использование метода 1Н ЯМР микротомографии для in situ исследования испарения жидкости из объектов, моделирующих пористое тело. Докл. РАН, т. 376, 2001, с. 1—5.
- Koptyug I. V., Khitrina L. Yu., Parmon V. N., Sagdeev R. Z. NMR imaging of mass transport and related phenomena in porous catalysts and sorbents. Magn. Reson. Imaging, v. 19, 2001, p. 531—534.
- Koptyug I. V., Ilyina L. Yu., Matveev A. V., Sagdeev R. Z., Parmon V. N., Altobelli S. A. Liquid and gas flow and related phenomena in monolithic catalysts studied by 1H NMR microimaging. Catal. Today, v. 69, 2001, p. 385—392.
- Коптюг И. В., Ильина Л. Ю., Матвеев А. В., Пармон В. Н., Сагдеев Р. З. Применение ЯМР-микротомографии для решения актуальных задач катализа. Хим. физика, т. 21, 2002, с. 68—78.
- Koptyug I. V., Matveev A. V., Altobelli S. A. NMR studies of hydrocarbon gas flow and dispersion. Appl. Magn. Reson., v. 22, 2002, p. 187—200.
- Коптюг И. В., Сагдеев Р. З. Современные физико-химические приложения ЯМР-томографии. Специфика метода и его применение для исследования объектов, содержащих жидкости. Успехи химии, т. 71, № 7, 2002, с. 672—699.
- Коптюг И. В., Сагдеев Р. З. Применение метода ЯМР-томографии для исследования процессов транспорта вещества. Там же. № 10, 2002, с. 899—949.
- Медведев Н. Н., Волошин В. П. Использование межатомных пустот для исследования структуры на средних масштабах в компьютерных моделях жидкостей и стекол. Там же, № 5, 2002 (в печати).
- Коробейников Ю. Г., Глазнев В. Н. Эффект Гартмана. Область существования и частоты колебаний. ПМТФ, т. 42, № 4, 2001. с. 62—67.
- Коробейников Ю. Г., Федоров А. В. Об экстракции воды из капиллярного образца в акустическом поле. ИФЖ, т. 76, № 1, 2003, с. 7—10.
- Aristov Yu. I., Restuccia G., Cacciola G., Parmon V. N. A family of new working materials for solid sorption air conditioning systems. Appl. Therm. Eng., v. 22, 2002, p. 191—204.
 Оглавление Оглавление |
Далее 
|





