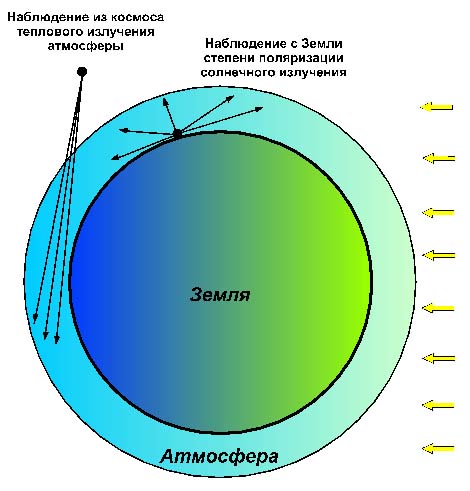
Рис. 1. Обратные задачи атмосферной оптики.
Fig. 1. Inverse problems of atmospheric optics.
Координатор: член-корр. РАН Михайлов Г. А.
Исполнители: ИВМиМГ, ИМ, ИВТ, ИТ, ИТПМ СО РАН
Построены новые весовые модификации статистического моделирования ансамбля взаимодействующих частиц для приближенного решения нелинейного уравнения Больцмана. Это дает возможность эффективно изучать зависимость вычисляемых функционалов от параметров задачи. Разработаны вычисление параметрических производных от интенсивности поляризованного солнечного излучения и решение обратных задач атмосферной оптики по наблюдениям с Земли методом Монте-Карло. Предложен новый метод для определения объемной концентрации газооборазных веществ по наблюдениям теплового излучения атмосферы со спутника (рис. 1). Новизна метода состоит в последовательном разрешении специально построенной треугольной системы нелинейных уравнений с использованием стохастической регуляризации. Разработаны весовые методы Монте-Карло для оценки параметров временных асимптотик в теории переноса излучения на основе использования функций Грина и преобразования Фурье, получены новые оценки помехи обратного рассеяния.
 |
Рис. 1. Обратные задачи атмосферной оптики. Fig. 1. Inverse problems of atmospheric optics. |
Для эффективного использования многопроцессорных вычислительных кластеров разработаны параллельные алгоритмы метода ПСМ. Решен ряд новых задач гиперзвуковой аэродинамики разреженного газа в околоконтинуальном режиме с учетом эффектов реального газа (возбуждение внутренних энергетических молекулярных мод и химические реакции). Проведены исследования ародинамики космической станции “Мир” при контролируемом спуске с орбиты (рис. 2).
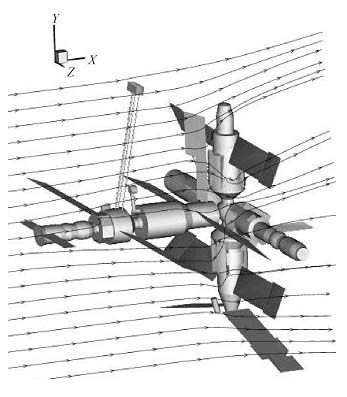 |
Рис. 2. Станция "Мир" - линии тока на высоте 110 км. Fig. 2. The streamlines around the MIR space station at an altitude of 110 km. |
Получили значительное развитие конструктивные методы, теория и компьютерное моделирование многомерных линейных и нелинейных обратных задач для кинетических уравнений, непосредственно связанных с проблемами идентификации, управления, распознавания образов, томографии. Получены и обоснованы новые представления решений кинетических уравнений типа Больцмана, дающие возможность получать соотношения для искомых величин (источников излучения, коэффициентов поглощения, индикатрис рассеяния и других характеристик сред) в обратных задачах. Предложены и реализованы новые численные методы решения задач векторной томографии (рис. 3), состоящих в определении правых частей линейного кинетического уравнения, описывающего неоднородные или анизотропные среды.
 |
Рис. 3. Реконструкция 1-й компоненты оригинала соленоидального тензорного поля 2-й валентности. В данные внесен шум с уровнем в 11 %, точность восстановления 12,5 %. Fig. 3. Reconstruction of the 1-st component of an original of the solenoidal tensor field of the 2-nd degree. A noise of the level of 11 % is imported into the data, an accuracy of the reconstruction is 12.5 %. |
Для полного кинетического уравнения Больцмана со степенным потенциалом межмолекулярного взаимодействия в форме его Фурье-преобразования по скоростным переменным построена оптимальная система подалгебр допустимой девятипараметрической группы и исследованы инвариантные решения от одной и двух независимых инвариантных переменных. Разработаны эффективные численные алгоритмы и реализующие их программы для решения самосогласованной системы уравнений Власова—Максвелла на неструктурированных сетках в областях сложной формы. На основе системы кинетических уравнений Власова для ионов и электронов методом “частиц-в-ячейках” выполнено численное моделирование взаимодействия мощного лазерного импульса с водородной плазмой. В расчетах воспроизведен ряд новых физических эффектов. На основе кинетического уравнения Власова—Лиувилля методом “частиц-в-ячейках” численно исследована эволюция самогравитирующего газопылевого диска (рис. 4), представляющая большой интерес для астрофизики.
 |
Рис. 4. Модель формирования галактической структуры. Fig. 4. Formation of the Galaxy structure. |
Список основных публикаций
Всего по проекту опубликовано более 40 статей в рецензируемых журналах.
 Оглавление Оглавление |
Далее 
|