ФУНДАМЕНТАЛЬНЫЕ ПРОБЛЕМЫ ГИДРОМЕХАНИКИ
И ТЕПЛОМАССОПЕРЕНОСА В УСЛОВИЯХ МИКРОГРАВИТАЦИИ
Координатор: член-корр. РАН Пухначев В. В.
Исполнители: ИГиЛ, ИТ, ИВМ, ТФ ИТПМ СО РАН
Исследования по гидродинамике и теплообмену при пониженной гравитации стимулируются, с одной стороны, потребностями космической техники, а с другой — необходимостью научного обеспечения технологических экспериментов на орбите. Почти все технологические процессы имеют дело с неизотермическими текучими средами, они осложнены наличием границ раздела жидкость — газ и поверхностей фазового перехода. Понимание основных закономерностей многофазных течений и фазовых переходов при пониженной гравитации важно и для развития наземных технологий, использующих тонкие пленки жидкости, эмульсии с близкими плотностями несущей и дисперсной фаз, расплавы малых объемов.
Выполнено экспериментальное и теоретическое исследование деформации границы раздела при течении пленки жидкости по вертикальной поверхности с неоднородным нагревом. Пример термокапиллярной деформации поверхности пленки изображен на рис. 1. Изучено влияние угла наклона пластины к горизонту и начальной температуры жидкости на длину волны регулярных структур. Установлено, что при формировании струй в области двумерных и трехмерных волн помимо термокапиллярного механизма существен капиллярно-волновой механизм. На основе серий расчетов изучена зависимость полей скорости, температуры и формы поверхности пленки от управляющих параметров процесса.
 |
|
Рис. 1. Рельеф свободной поверхности при Re = 2, q = 0,84 Вт/см2.
а - шлирен-изображение пленки, б - расчет положения ее поверхности.
Fig 1. A contour of a free surface at Re = 2, q = 0,84 W/sm2.
а - shliren-image of a film, б - calculation of a position of the surface.
|
Выведены уравнения тепловой гравитационной конвекции слабосжимаемой жидкости в замкнутом объеме. Показано, что в результате последовательных предельных переходов из этих уравнений можно получить как уравнения микроконвекции, так и уравнения Обербека—Буссинеска. Решена в линейном приближении задача описания переходного процесса, содержащего быстроосциллирующие функции времени.
Исследована устойчивость равновесного состояния плоского слоя, ограниченного твердыми стенками или одной свободной границей, в модели микроконвекции. Изучена устойчивость стационарных течений в плоском слое для линейного и экспоненциального распределений температуры поперек слоя.
Проведены экспериментальные исследования условий устойчивости структуры жидкодисперсных сред (эмульсий и суспензий) в импульсных градиентных температурных полях. В координатах плотность теплового потока — продолжительность теплового импульса построена гиперболическая кривая, разделяющая области устойчивости и неустойчивости (рис. 2).
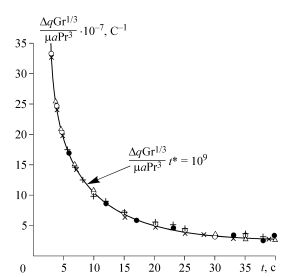 |
Рис. 2. Критериальная кривая A=Δqt*Gr1/3(αμPr)-1=109 разделяющая области устойчивости A<109и неустойчивости A>109 структуры эмульсий и суспензий при воздействии на них локального теплового импульса удельной мощностью тепловыделения до 5 Дж*см-2*с-1.
O,x,+,· - экспериментальные данные для различных видов эмульсий и суспензий.
Fig. 2. A criteria curve A=Δqt*Gr1/3(αμPr)-1=109 parting fields (areas) of a stability A<109 and instability A>109 structures of emulsions and suspensions at action on them of local thermal impulse by a specific power up to 5 J*sm-2*s-1.
O,x,+,· - experimental data for the different types of emulsions and suspensions.
|
Список основных публикаций
- Кабов О. А., Легро Ж. К., Марчук И. В., Шейд Б. Деформация свободной поверхности в движущемся локально нагреваемом тонком слое жидкости// Изв. РАН. МЖГ. 2001. № 2. С. 200—208.
- Бекежанова В. Б. Об одном стационарном решении уравнений микроконвекции в вертикальном слое// ПМТФ. 2001. Т. 42, № 3. С. 63—71.
- Кабов О. А., Кузнецов В. В., Марчук И. В., Пухначев В. В., Чиннов Е. А. Регулярные структуры при термокапиллярной конвекции в движущемся тонком слое жидкости// Поверхность, рентгеновские, синхротронные и нейтронные исследования. 2001. № 9. С. 83—89.
- Журавлева Е. Н., Петрова А. Г. Асимптотическая модель управления составом материала, получаемого в результате затвердевания эмульсии// Изв. АлтГУ. 2001. № 1. С. 16—19.
- Petrova A. G., Pukhnachev V. V., Zhuravleva E. N. Solidificatication of emulsion moving under effect of thermocapillary torces and microacceleration// Nonlinear Boundary Value Problems. 2001. N 10. P. 142—150.
- Андреев В. К., Бекежанова В. Б. Об устойчивости равновесия плоского слоя в модели микроконвекции// ПМТФ. 2002. Т. 43, № 2. С. 43—53.
- Гапоненко Ю. А., Захватаев В. Е. Небуссинескова тепловая конвекция в условиях микрогравитации при неоднородном подогреве// ПМТФ. 2002. Т. 43, № 6. С. 46—53.
- Пухначев В. В. Иерархия моделей в теории конвекции// Записки научных семинаров ПОМИ. 2002. Т. 288. С. 152—177.
- Кабова Ю. О., Кузнецов В. В. Стекание неизотермического тонкого слоя жидкости с непостоянной вязкостью// ПМТФ. 2002. Т. 43, № 6. С. 134—141.
- Стебновский С. В. Исследование устойчивости структуры эмульсии при воздействии на нее локального теплового импульса// Теплофизика и аэромеханика. 2002. Т. 9, № 1. С. 113—119.
- Сhinnov E. A., Kabov O. A., Marchuk I. V., Zaitsev D. V. Heat transfer and breakdown of subcooled falling liquid film on a vertical middle size heater// Int. J. Heat and Technology. 2002. Vol. 20, N 1. p. 69—78.
- Kabov O. A., Scheid B., Sharina I. A., Legros J.-C. Heat transfer and rivulet structures formation in a falling thin liquid film locally heated// Int. J. Therm. Sci. 2002. Vol. 41. p. 664—672.
Всего опубликовано более 20 статей в рецензируемых журналах.
 В оглавление В оглавление |
Далее 
|



