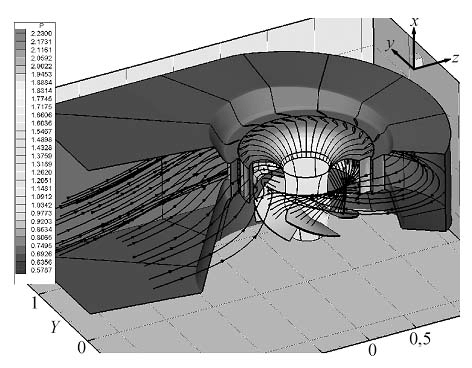
Рис. 1. Пример расчета течения в проточной части гидротурбины.
Fig. 1. Example of calculation of flow in a blading section of a hydraulic turbine.
Координатор: член-корр. РАН Плотников П. И.
Исполнители: ИВМ, ИВТ, ИГиЛ, ИМ, ИТПМ, ИТ, НФ ИВЭП СО РАН,
ИПМТ ДВО РАН, НГТУ (Новосибирск), НГТУ (Нижний Новгород)
Разработана методика моделирования нестационарных периодических гидродинамических процессов в различных гидроустройствах. Создан аппарат сплайн-функций, существенно повышающий точность и качество восстановления поверхностей гидроустройств. Предложены новые методы аппроксимации функций трех переменных по данным, заданным с погрешностью в хаотически расположенных точках. Выполнены расчеты течений в проточной части гидротурбины с учетом взаимодействия ротора и статора (рис. 1).
 |
Рис. 1. Пример расчета течения в проточной части гидротурбины. Fig. 1. Example of calculation of flow in a blading section of a hydraulic turbine. |
Предложен метод замыкания математических моделей турбулентности. Получены новые инвариантные решения эволюционных уравнений. Построены численные модели закрученных осесимметричных турбулентных следов. Исследовано вырождение дальних турбулентных следов. Получены законы автомодельного вырождения дальнего турбулентного следа за самодвижущимся телом. Выполнены расчеты взаимодействия турбулентного пограничного слоя на пластине с падающим косым скачком уплотнения (рис. 2, 3). Исследованы безотрывные течения, течения с локальной и крупномасштабной отрывной зонами.
 |
Рис. 2. Экспериментальное поле плотности. Fig. 2. Experimental field of density. |
Проведена групповая классификация уравнений Навье—Стокса для сжимаемого вязкого теплопроводного газа. Впервые показано, что при специальном виде уравнений состояния система может допускать проективное преобразование.

|
Рис. 3. Расчетное поле плотности. Fig. 3. Computational field of density. |
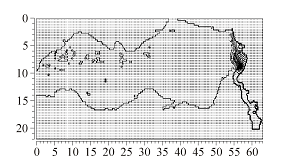
Разработаны новые математические модели экологических и гидрофизических процессов в реальных водных объектах. Предложена численная модель турбулентных течений и процессов переноса примеси в равнинном водохранилище. Получены векторные поля скорости течений и распределения фенола, поступающего с водами р. Бердь (рис. 4).
 |
|
Рис. 4. Результат моделирования распространения фенола в акватории Обского водохранилища. Fig. 4. Results of simulation of propagation of Phenolum in a water area of the Ob artifitial sea. |
Развиты новые аналитические подходы к исследованию точных нелинейных постановок задач о волновых движениях жидкости. Изучены эволюционные системы квазилинейных интегродифференциальных уравнений, являющиеся обобщением классической модели теории мелкой воды и возникающие при исследовании длинных волн в завихренной жидкости. Построен новый класс точных решений этих систем.
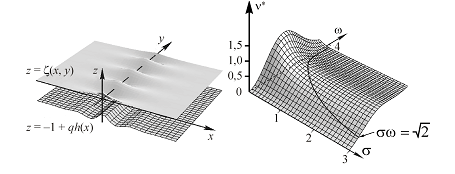
Исследована задача о трехмерных стационарных поверхностных волнах над подводным хребтом в точной нелинейной формулировке. Доказано существование бегущих волн над подводным хребтом, амплитуда которых периодична вдоль хребта и экспоненциально затухает в перпендикулярном направлении (рис. 5).
 |
|
Рис. 5. Поверхностные волны над подводным хребтом. Fig. 5. Surface waves above underwater crest. |
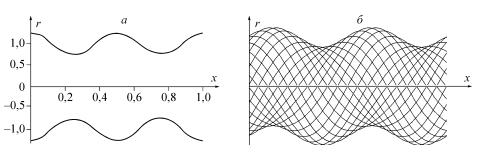
Исследована гидродинамика крупных кровеносных сосудов. Предложена нелинейная модель завихренного осесимметричного течения жидкости в длинной цилиндрической трубке с упругими изотропными стенками (рис. 6). Определен непрерывный и дискретный спектр скоростей распространения возмущений в осесимметричных завихренных движениях.
 |
|
Рис. 6. Перистальтическая (а) и винтовая (б) деформации стенок эластичной трубки. Fig. 6. Peristaltic (а) and propeller (б) deformations of walls of an elastic pipe. |
Экспериментально исследовано взаимосвязанное движение жидкости и цилиндра (рис. 7). Цилиндр под воздействием набегающего потока совершает малые колебания с тремя степенями свободы: вращательные колебания и колебания в горизонтальном и вертикальном направлениях.
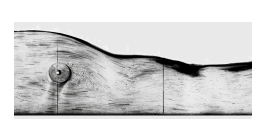 |
Рис. 7. Гидродинамический след за колеблющимся цилиндром. Fig. 7. Hydrodynamic trace behind an oscillating cylinder. |
Найдено распределение амплитуд колебаний упругих напряжений и прогибов под действием набегающей волны для пластины усложненной конструкции, состоящей из двух различных частей или упруго соединенной с дном (рис. 8). Показано, что за счет присоединения перед основной упругой пластиной дополнительной жесткой пластины меньшего размера можно существенно уменьшить амплитуду колебаний основной пластины. Построено решение нестационарной задачи о поведении плавающей упругой круглой пластины под действием произвольной внешней нагрузки.
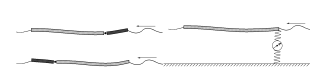 |
Рис. 8. Гашение колебаний плавающей упругой пластины. Fig. 8. Damping of oscillations of a floating elastic plate. |
Список основных публикаций
Всего опубликовано более 70 статей в рецензируемых журналах.
 В оглавление В оглавление |
Далее 
|