
Институт вычислительной математики и математической геофизики (ИВМиМГ)
Institute of Computational Mathematics and Mathematical Geophysics
Создан 24 мая 1964 г.
Адрес: 630090, Новосибирск, просп. ак. Лаврентьева, 6
Тел. (383 2) 34-33-53
Факс (383 2) 34-16-87
Е-mail: mikh@sscc.ru.
Директор – д.ф.-м.н. Михайленко Борис Григорьевич
Заместитель директора по науке – чл.-к. РАН Михайлов Геннадий Алексеевич
Общая численность института 360 чел.; н.с. – 176, ак. – 1, чл.-к. РАН – 2, д.н. – 33, к.н. – 99.
Основные научные направления:
- вычислительная математика;
- математическое моделирование и методы прикладной математики в геофизике.
Лаборатории:
Численного моделирования сейсмических полей (д.ф.-м.н. Б.Г. Михайленко)
Математического моделирования волн цунами (к.ф.-м.н. В.К. Гусяков)
Информационных технологий вычислитель ной геофизики (д.ф.-м.н. Г.Н. Ерохин)
Геофизических вычислительных комплексов (д.т.н. Б.М. Глинский)
Цифровых методов обработки геофизичес кой информации (д.т.н. М.С. Хайретдинов)
Обработки изображений (д.т.н. В.П. Пяткин)
Параллельных алгоритмов и структур (к.т.н. С.В. Пискунов)
Синтеза параллельных программ (д.ф.-м.н. В.Э. Малышкин)
Анализа и машинной графики (д.ф.-м.н. А.М. Мацокин)
Системного моделирования (д.ф.-м.н. М.И. Нечепуренко)
Математического моделирования информационных сетей (д.ф.-м.н. В.К. Попков)
Прикладных систем (к.т.н. С.В. Бредихин)
Математического моделирования гидросферы (д.ф.-м.н. В.И. Кузин)
Динамики климата (д.ф.-м.н. А.А. Фоменко)
Математического моделирования гидродинамических процессов в природной среде (д.ф.-м.н. В.В. Пененко)
Методов Монте-Карло (чл.-к. РАН Г.А. Михайлов)
Оптики дисперсных сред (д.ф.-м.н. Б.А. Каргин)
Стохастических задач математической физики (д.ф-м.н. К.К. Сабельфельд)
Численного анализа стохастических дифференциальных уравнений (д.ф.-м.н. С.С. Артемьев)
Вычислительной физики (д.ф.-м.н. В.П. Ильин)
Математических задач химии (д.ф.-м.н. Ю.М. Лаевский)
Математических задач сейсмологии (ак. А.C. Алексеев)
Вибросейсмических исследований (к.ф.-м.н. А.Н. Кремлев)
Основные научные результаты
Для решения задач, описывающих процессы с существенной пространственно-временной разномасштабностью предложен и исследован ряд новых явных разностных схем с различными временными шагами для различных групп переменных. Введенный класс схем позволяет осуществить эффективное распараллеливание алгоритмов при решении сложных нестационарных задач и хорошо подходит для решения задач с локальными неустойчивостями, например математических задач теории горения.
Разработан метод световых сеток в лучевой трассировке для расчета фотореалистических изображений пространственных сцен. Метод позволяет ускорить процесс расчета теней, строить мягкие тени и имитировать основные эффекты переотражений диффузного освещения (рис. 1).

Рис. 1. Пример мягких теней, получаемых с применением световых сеток.
Fig. 1. Example of soft shadows produced by Light Meshes algorithm.
Разработан и апробирован комплекс климатических моделей Мирового океана, позволяющий проводить долговременные расчеты по формированию режимов и изменчивости глобального климата океана под действием естественных и антропогенных факторов в масштабах тысячелетий. Модели обладают различной физической полнотой и особенностями дискретизации, что позволяет использовать различные версии для реализации широкого диапазона климатических экспериментов, включающих в себя распространение растворенных в морской воде парниковых газов (рис. 2).
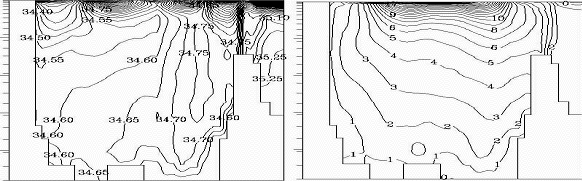
Рис. 2. Зонально средние соленость и температура в модели климата Мирового океана.
Fig. 2. Zonally averaged salinity and temperature in the World ocean model.
Предложен и алгоритмически реализован новый подход к построению высокоэффективных алгоритмов совместного использования математических моделей и данных измерений для изучения природных процессов в климатической системе. Метод основан на вариационных принципах в комбинации с методом расщепления. Алгоритмы обеспечивают усвоение данных в реальном времени по мере их поступления и позволяют оперативно настраивать целевые функционалы в зависимости от текущего состава наблюдений так, чтобы использовать всю имеющуюся информацию от различных наблюдательных систем.
Разработана наиболее полная на сегодняшний день экспертная база данных по наблюдениям цунами в Тихом океане, содержащая сведения о почти 1 500 цунамигенных событиях, происшедших в Тихоокеан ском регионе за весь период до инструментальных и инструментальных наблюдений (с 47 г. до н.э по 2000 г.). База снабжена специализированной графической оболочкой, построенной на принципах ГИС-технологий и предоставляющей пользователю удобные средства для выборки, визуализации и обработки данных (рис. 3). База данных вместе с графической оболочкой распространяется на CD-ROMе «Tsunamis in the Pacific, 47 B.C. – 2000 A.D.», выпущенном совместно с Межправительственной океанографической комиссией (МОК) ЮНЕСКО. Web-версия базы данных поддерживается на сервере лаборатории цунами ИВМиМГ СО РАН (http://tsun.sscc.ru/htdbpac).
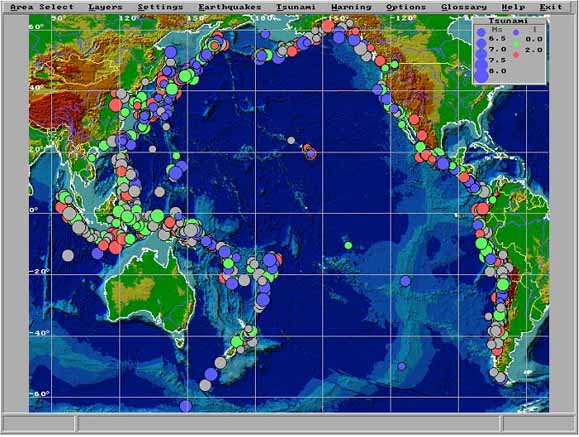
Рис. 3. Пример работы графической оболочки экспертной базы данных по проблеме цунами - карта очагов тихоокеанских цунами (за период с 47 г. до н.э. по 2000 г.).
Fig. 3. Example of the epicenters of historical tsunamigenic earthquakes occurred in the Pacific from 47 year b.p. to 2000.
Для многопроцессорной ЭВМ «RM600-E30» реализована первая очередь параллельной системы моделирования. Входной язык системы моделирования – процессно-ориен тированный язык дискретного имитацион ного моделирования, реализованный как пакет на языке С++. Взаимодействие процессов реализовано с помощью механизма передачи сообщений. Разработан и реализован алгоритм синхронизации параллельных процессов в модельном времени.
В 2001 г. институтом опубликовано: статей в рецензируемых журналах – 143, монографий – 12.
Институт вычислительного моделирования (ИВМ)
Institute of Computational Modeling
Создан 17 января 1975 г.
Адрес: 660036, Красноярск, Академгородок
Тел./факс (391 2) 43-27-56
E-mail: sek@icm.krasn.ru
Директор – чл.-к. РАН Шайдуров Владимир Викторович
Заместители директора по науке:
д.ф.-м.н. Горбань Александр Николаевич
д.т.н. Москвичев Владимир Викторович
Общая численность института 146 чел.; н.с. – 82, чл.-к. РАН – 1, д.н. – 22, к.н. – 51.
Основное научное направление:
- методы математического моделирования и интеллектуальные информационные системы.
Научные подразделения:
Отделы:
Нелинейных задач механики (д.ф.-м.н. В.К. Андреев)
Вычислительной физики (д.ф.-м.н. Н.Я. Шапарев)
Прикладной информатики (д.т.н. Л.Ф. Ноженкова)
Машиноведения (д.т.н. В.В.Москвичев)
Хозрасчетная лаборатория распределенных информационных систем (И.И.Сапожков)
Дискретной математики (д.ф.-м.н. О.Ю. Воробьев)
Вычислительной математики (чл.-к. РАН В.В. Шайдуров)
Моделирования неравновесных систем (д.ф.-м.н. А.Н. Горбань)
Вычислительных моделей в гидрофизике (д.ф.-м.н. В.М. Белолипецкий)
Вычислительной механики деформируемых сред (д.ф.-м.н. В.М. Садовский)
Основные научные результаты
С помощью вариационной формулировки граничных условий контактного взаимодействия упругопластических тел с учетом трения разработан новый вычислительный алгоритм, обладающий рядом преимуществ перед известными. Алгоритм обеспечивает выполнение дискретных ограничений в зоне контакта, условия неотрицательности контактного давления и условия противополож ной направленности касательной скорости и касательного напряжения при проскальзы вании (рис. 1). Показано, что схема простого сдвига, используемая для описания деформированного состояния стружки при механической обработке резанием, применима только в случае достаточно малого переднего угла инструмента. В задаче косого соударения пластин дано численное обоснование известной гипотезы о забегании пластической зоны вперед по отношению к точке контакта при скорости этой точки, меньшей скорости пластических ударных волн. Получена картина волнообразования при сварке взрывом из-за механической потери устойчивости поверхностного слоя.
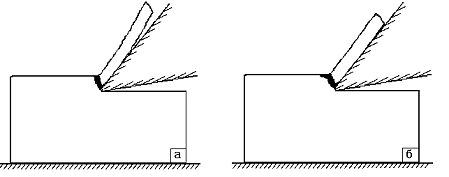
Рис. 1. Конфигурация пластической зоны при резании (а – результаты без учета трения, b – с трением).
Fig. 1. The configuration of plastic zone under cutting (a – results without friction, b – with friction).
С развитием космического аппарато-строения большое значение приобретает переход к проектированию и изготовлению космических аппаратов (КА) нового поколения, имеющих негерметичное исполнение. Такие КА имеют меньший вес, повышенную надежность и срок активного существования до 15 лет. Вместе с тем такая конструкция КА предъявляет жесткие требования к обеспечению теплового режима. Институтом вычислительного моделирования разработан пакет прикладных программ для расчета тепловых режимов космических аппаратов негерметичного исполнения, движущихся по произвольной орбите, с учетом эффективной теплоемкости конструкции и приборов, теплового сопротивления контактных узлов и переменной теплопроводности радиационных панелей. Пакет прикладных программ используется в НПО ПМ им. академика М.Ф. Решетнева при разработке новых конструкций спутников.
На основании технологии визуализации многомерных данных получена информационная модель распределения участков генома в пространстве частот непересекающихся триплетов. Структура распределения отражает факт наличия в кодирующих областях выделенной кодирующей фазы.
Преобразование последовательности ДНК в таблицу многомерных данных осуществлялось методом скользящего окна; при этом объектами служили центральные позиции окна, а признаками – частоты непересекающихся триплетов (рис. 2). На основе анализа распределения данных методом упругих карт получено разделяющее правило для распознавания белок-кодирующих участков в геноме. Найдена оптимальная ширина скользящего окна, на которой различие между кодирующими и некодирующими участками максимально. Разработан метод автоматической идентификации белок-кодирующих участков в геноме. Точность распознавания для генома дрожжей составила 85 %, т.е. сравнима с точностью современных методов распознавания. Однако достоинство предлагаемого метода заключается в его простоте, наглядности и естественной интерпретации.
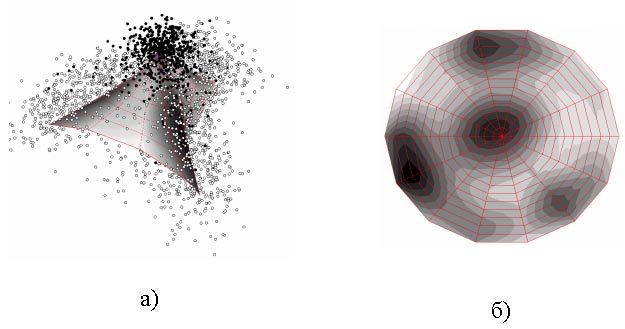
Рис. 2. Применение метода упругих карт для визуализации и анализа распределения многомерных данных: а – упругая карта, моделирующая данные (геном Prototheca wickerhamii): визуализация в подпространстве трех первых главных компонент (светлые точки – для окон с центром в белок-кодирующих участках, темные – для окон с центром в некодирующих участках); b – визуализация плотности распределения точек во внутренних координатах упругой карты: центральный кластер соответствует некодирующим участкам, три боковых кластера – белок-кодирующим участкам в трех разных фазах.
Fig. 2. Visualization and analysis of multidimensional data distribution by the method of elastic maps: a – distribution of DNA sites in the triplet frequencies space and the analog elastic map visualized in the subspace of three principal vectors, b – the density of data distribution shown in the inner coordinates of elastic map: the central cluster corresponds to non-coding regions of DNA, genes in three different phases form three other clusters.
В 2001 г. институтом опубликовано: статей в рецензируемых журналах – 88, монографий – 10.
Институт динамики систем и теории управления (ИДСТУ)
Institute of System Dynamics and Control Theory
Cоздан 11 сентября 1980 г.
Адрес: 664033, Иркутск, ул. Лермонтова, 134, а/я 1233
Тел. (395 2) 46-43-00
Факс (395 2) 51-16-16
E-mail: snvas@icc.ru
Директор – чл.-к. РАН Васильев Станислав Николаевич
Заместители директора по науке:
д.ф.-м.н. Батурин Владимир Александрович
к.т.н. Бычков Игорь Вячеславович
к.т.н. Максимкин Николай Николаевич
Общая численность института 160 чел.; н.с. – 71, чл.-к. РАН – 1, д.н. – 16, к.н. – 48.
Основные научные направления:
- научные основы теории и методов управления;
- математические методы и информационные технологии исследования динамических систем.
Лаборатории:
Теории сложных управляемых систем (к.ф.-м.н. Р.И. Козлов)
Теории логико-динамических и алгебро-диф ференциальных моделей (к.ф.-м.н. А.В. Лакеев)
Системного анализа и методов оптимально го управления (д.ф.-м.н. В.А. Батурин)
Методов глобальной оптимизации (д.ф.-м.н. А.С. Стрекаловский)
Исследования операций (д.ф.-м.н. В.П. Булатов)
Динамики нелинейных систем с распределен ными параметрами (к.ф.-м.н. Г.А. Рудых)
Дифференциальных включений и оптимизации (д.ф.-м.н. А.А.Толстоногов)
Устойчивости движения (д.ф.-м.н. В.Д. Иртегов)
Методов автоматизации исследований управляемых систем (д.т.н. Г.А. Опарин)
Прикладной логики (д.ф.-м.н. В.И. Мартьянов)
Методов и систем искусственного интеллекта (к.т.н. И.В. Бычков)
Методов представления и обработки информации (к.т.н. А.Е. Хмельнов)
Телекоммуникационных и вычислительных систем (к.ф.-м.н. С.В. Бурносов)
Основные научные результаты
Разработана качественная теория дифференциальных и разностных уравнений с условиями монотонности. Получены теоремы о дифференциальных и интегральных неравенствах, условия максимальности решений, полунепрерывности по начальным данным и возмущениям правой части, установлены инвариантные множества, связанные с областями знакопостоянства правых частей. Предложен принцип сравнения второго уровня, на основе которого получены достаточные условия существования наиболее важных динамических свойств типа устойчивости, ограниченности, притяжения с количественными оценками показателей динамики (предельных множеств, областей притяжения и др.). Исследованные классы уравнений применяются в качестве систем сравнения в методе векторных функций Ляпунова, а также описывают динамические процессы в экономике, биологии, теории игр и др.
Разработана теория качественного анализа динамики автоматных сетей и управления сетями при возмущениях. В литературе в основном известны результаты для моделей в форме так называемых синхронных или последовательных итераций и, как правило, с симметричными взаимодействиями элементов. Созданная теория ориентирована на общий тип взаимодействия и механизм срабатывания в форме блочно-последова тельных итераций. Кроме того, допускается вхождение в сеть элементов задержки на определенную глубину памяти. При этом в отличие от случаев симметричного взаимодействия не гарантируется сходимости процессов к предельным циклам или неподвижным точкам. Изучены свойства притяжения, достижимости целевых состояний, связности целевого множества и др.
На базе интегрированной коммуникационно-вычислительной сети Иркутского научного центра СО РАН и организаций Иркутского регионального научно-образовательного комплекса с волоконно-оптическими линиями связи (100 Мбит/с) создана корпоративная геоинформационно-вычислительная сеть (рис. 1). При создании сети использованы интернет-технологии корпоративных систем распределенных вычислений. В частности, в визуализатор данных системы картографо-математического анализа территорий (КАМАТ) были добавлены функции OLE-сервера, что обеспечило многопользовательский доступ к данным для их совместного использования клиентами корпоративной сети (выбор просматриваемых карт, перемещение по ним, формирование тематических слоев, масштабирование, выполнение запросов к тематическим базам данных и т.д.). Для интеграции с WWW-сервером Администрации Иркутской области разработан комплекс программ как OLE-клиентов визуализатора. Интеллектуализация сети достигается с использованием оригинальных средств поддержки конструктивных логических выводов, более мощных, чем ПРОЛОГ. Примером такой интеллектуализации является автоматизация построения уравнений динамики с отображением на картах процессов лесопользования с учетом рубок, насаждений, пожаров и других воздействий на лесные ресурсы.
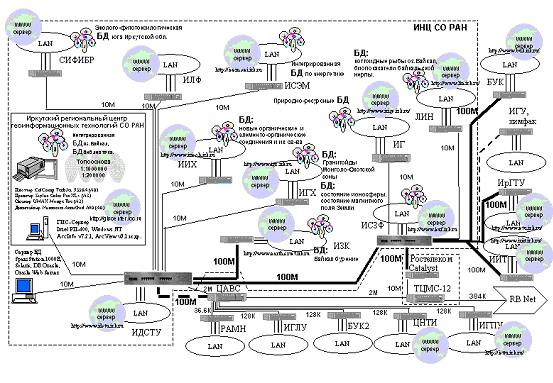
Рис. 1. Схема информационно-корпоративной сети Иркутского научного центра.
Fig. 1. Corporate network of Irkutsk Science Center.
В 2001 г. институтом опубликовано: статей в рецензируемых журналах – 59, монографий – 5.
 В оглавление В оглавление |
Далее 
|
 Ваши комментарии Обратная связь |
![[SBRAS]](/gif/s_sigma.gif)
[СО РАН] [ИВТ СО РАН] |
© 1996-2014, Сибирское отделение Российской академии наук, Новосибирск
© 1996-2014, Институт вычислительных технологий СО РАН, Новосибирск
Дата последней модификации: Friday, 05-Jul-2002 14:42:47 NOVST