§ 6. Задачи с ограничениями типа равенств

В этом параграфе рассматривается одна из простейших задач условной оптимизации. Проводится теоретическое исследование. Описываются методы решения

6.1. Постановка задачи.

Напомним, что общая задача условной оптимизации выглядит так

f(x) → min,   x ∈ Ω,

где Ω — собственное подмножество R^m. Подкласс задач с ограничениями типа равенств выделяется тем, что множество Ω задается ограничениями вида

fi(x) = 0, где fi: Rm →R (i = 1, ..., k). Таким образом, Ω = {x ∈ Rm: fi(x) = 0, i = 1, ..., k}. В этом параграфе, как и в предыдущих, мы предполагаем, что все участвующие в рассмотрении функции достаточно гладкие. В общем случае множество Ω представляет собой гладкое (m–k)-мерное многообразие. Нам будет удобно писать у функции f индекс "0". Таким образом, задача оптимизации с ограничениями типа равенств записывается в виде f0(x) → min, (1) fi(x) = 0,   i = 1, ..., k. (2) Если обозначить теперь через f функцию на Rm со значениями в Rk, координатная запись которой имеет вид f(x) = (f1(x), ..., fk(x)), то (1)–(2) можно также записать в виде f0(x) → min,   f(x) = Θ. Геометрически задача с ограничениями типа 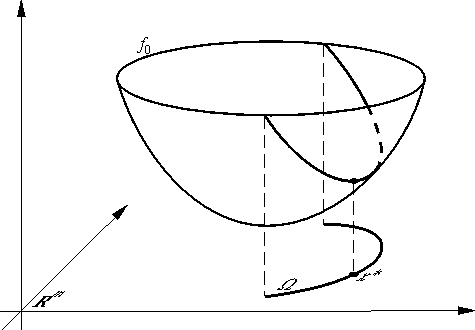равенств — это задача о поиске наинизшей точки графика функции f0 над многообразием Ω (см. рис. 19). Рис. 19. 6.2. Определения. Точки, удовлетворяющие всем ограничениям (т. е. точки множества Ω), обычно называют допустимыми. Допустимая точка x* называется условным минимумом функции f0 при ограничениях fi(x) = 0, i = 1, ..., k (или решением задачи (1)–(2)), если при всех допустимых точках x f0(x*) ≤ f0(x). (3) Если (3) выполняется только для допустимых x, лежащих в некоторой окрестности Vx* точки x*, то говорят о локальном условном минимуме. Естественным образом определяются понятия условных строгих локального и глобального минимумов. З а д а ч а  6.1. Имеет ли задача x21+ x22→ min, (x1 – 1)2 + x22= 1, (x1 + 1)2 + x22 = 1 решение? 6.3. Правило множителей Лагранжа. Описываемый ниже необходимый признак локального условного минимума был сформулирован Лагранжем. Определим F: Rm → Rk+1, положив F(x) = (f0(x), f1(x), ..., fk(x)). Заданная на Rm×Rk+1 скалярная функция Лагранжа M по определению принимает значения в R и задается равенством M(x, μ) = (μ, F(x)) =  k ∑ i = 0 μi fi(x)   (x ∈ Rm, μ ∈ Rk+1).  Координаты вектора μ, т. е. числа μ0, μ1, ..., μk называются множителями Лагранжа или двойственными переменными. Оказывается, имеет место следующая теорема, часто именуемая правилом множителей Лагранжа: Теорема. Пусть F ∈ C1 и x* — локальный условный минимум функции f0 при ограничениях fi(x) = 0 (i = 1, ..., k). Тогда найдется ненулевой вектор μ* такой, что x* является стационарной точкой функции x→ M(x, μ*): M′x(x, μ*)|x=x*=  k ∑ i = 0 μ*i f ′i(x*)= Θ.   6.4. Обсуждение правила множителей Лагранжа. Начнем с геометрической интерпретации. Пусть для наглядности m = 2, а k = 1. В соответствии с теоремой 6.3, если 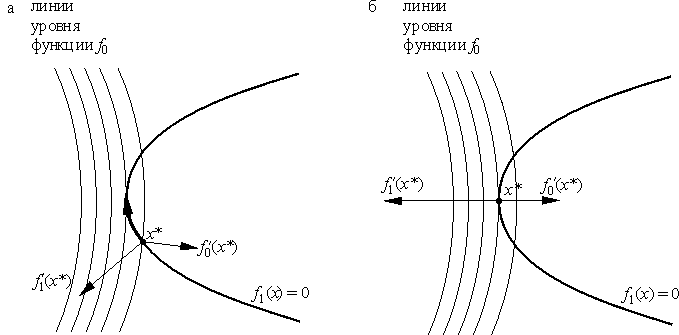x* — локальное решение задачи (1)–(2), то при некотором ненулевом μ* ∈ R2 μ*0 f ′0(x*)+ μ*1f ′1(x*)= Θ. (4) Это равенство означает, что векторы f ′0(x*)и f ′1(x*)линейно зависимы. Теперь заметим, что –f ′0(x*)указывает направление наискорейшего убывания функции f0. Поэтому, если (4) не выполняется, т. е. векторы f ′0(x*)и f ′1(x*)не коллинеарны, то по многообразию Ω = {x ∈ R2: f1(x*) = 0} можно сдвинуться, уменьшив значение f0 (в направлении, указанном жирной стрелкой на рис. 20а)). Если же x* — решение задачи (1)–(2), то этого сделать нельзя и (см. рис. 20б)) поэтому векторы f ′0(x*)и f ′1(x*)должны быть коллинеарны, т. е. при некотором μ* ≠ Θ должно выполняться равенство (4). Рис. 20. Правило множителей Лагранжа доставляет необходимое условие локального условного минимума и поэтому позволяет искать точки, "подозрительные" на экстремум. В самом деле, для нахождения точки (x*, μ*) ∈ Rm+k+1, т. е. для нахождения m + k + 1 неизвестных, мы имеем m + k уравнений f(x) = Θ,   M′x(x, λ)= Θ. Поскольку, очевидно, множители Лагранжа можно искать с точностью до постоянного множителя, то в общей ситуации этих уравнений хватает для отыскания x*. 6.5. Доказательство теоремы 6.3. Допустим противное: x* — локальное решение задачи (1)–(2), а нужного μ* не существует. Последнее означает, что векторы f0(x*), f1(x*), ..., fk(x*) линейно независимы, что, в свою очередь, влечет равенство rank ⌈ | | | | | | | | ⌊ ∂f0(x*) ∂x1 ··· ∂fk(x*) ∂x1 : ··· : ∂f0(x*) ∂xm ··· ∂fk(x*) ∂xm ⌉ | | | | | | | | ⌋  = k+1. Допустим, для определенности, что отличный от нуля минор (k+1)-го порядка образуют первые k + 1 строка этой матрицы: det ⌈ | | | | | | | | ⌊ ∂f0(x*) ∂x1 ··· ∂fk(x*) ∂x1 : ··· : ∂f0(x*) ∂xk+1 ··· ∂fk(x*) ∂xk+1 ⌉ | | | | | | | | ⌋  ≠ 0. (5) Обозначим (x1, ..., xk+1) через ξ, а (xk+2, ..., xm) — через η: x = (ξ, η), x* = (ξ*, η*). Обозначим далее f0(x*) через α* и определим оператор Φ: Rk+1 → Rk+1 формулой Φ(ξ) = F(ξ, η*). (6) Тогда, во-первых, Φ(ξ*) = (f0(x*), ..., fk(x*)) = (α*, 0, ..., 0) ≝ ζ* и, во-вторых, в силу (5), Φ′(ξ*) невырожден. В силу теоремы об обратном отображении (см. любой курс математического анализа) в некоторой окрестности Vζ* точки ζ* существует непрерывное обратное к Φ отображение Ψ: при всех ζ ∈ Vζ* Φ[Ψ(ζ)] = ζ. (7) В частности, это равенство имеет место для ζ = ζs = (s + α*, 0, ..., 0) при всех достаточно малых s. Положим xs = (Ψ(ζs), η*). Тогда (см. (6), (7)) (f0(xs), ..., fk(xs)) = F(xs) = F[Ψ(ζs), η*] = = Φ[Ψ(ζs)] = ζs = (s + α*, 0, ..., 0). Таким образом, при достаточно малых s, во-первых, f0(xs) = s + f0(x*) (8) и, во-вторых, f1(xs) = ... = fk(xs) = 0. Последнее равенство означает, что точки xs являются допустимыми, а (8) (если взять s достаточно малым и отрицательным) — что x* не является условным локальным минимумом. Полученное противоречие доказывает теорему. 6.6. Обсуждение доказательства. Основную идею доказательства, приведенного выше можно, немного модифицировав, интерпретировать так. Разобьем переменные xi на две группы (y, z) ∈ Rk×Rm–k так, чтобы из уравнения (2), т. е. из уравнения f(y, z) = Θ можно было выразить y через z: y = φ(z). Это можно сделать, поскольку f(y*, z*) = Θ, а f ′y(y*, z*)= Θ невырожден. Тогда задача (1)–(2) записывается в виде безусловной задачи f0(φ(z), z) → min,   z ∈ Rm–k. (9) Теорема Ферма для задачи (9) при этом порождает теорему 6.3. З а д а ч а  6.2. Проведите аккуратные рассуждения. 6.7. Регулярные точки. Допустимая точка x задачи (1)–(2) называется регулярной, если векторы {f ′i(x)}ki=1линейно независимы. Оказывается, что если x* — регулярная точка минимума, то в векторе μ* можно считать μ*0 считать ненулевым, а поскольку множители Лагранжа определяются с точностью до множителя, можно считать, что μ*0 = 1. Чтобы сформулировать это утверждение более точно, введем следующие обозначения. Пусть λ ∈ Rk, а функция Лагранжа в регулярном случае определяется равенством L(x, λ) = f0(x) + (λ, f(x)) = f0(x) +  k ∑ i = 1 λi fi(x)   (x ∈ Rm, λ ∈ Rk). Очевидно, L(x, λ) = M(x, μ), где μ = (1, λ). 6.8. Теорема (правило множителей Лагранжа в регулярном случае). Пусть F ∈ C1, а x* — регулярное локальное решение задачи (1)–(2). Тогда найдется ненулевой вектор λ* ∈ Rk такой, что L′x(x*, λ*)= Θ. Д о к а з а т е л ь с т в о.  Покажем, что теоремы 6.3 и 6.8 вытекают друг из друга (для доказательства теоремы 6.8 достаточно, разумеется, импликации "теорема 6.3 ⇒ теорема 6.8"; однако для полноты изложения мы докажем и обратное утверждение). Итак, пусть x* — регулярная точка минимума, а μ* — вектор, фигурирующий в теореме 6.3. Тогда, если μ*0 = 0, то в силу этой теоремы Θ = M′x(x*,μ*) =  k ∑ i = 0 μ*if ′i(x*)=  k ∑ i = 0 μ*if ′i(x*),  а поскольку не все μ*i (i = 1, ..., k) равны нулю, последнее равенство противоречит регулярности x*. Поэтому μ*0 ≠ 0. Теперь в качестве искомых λ*iможно взять μ*i/μ*0: L′x(x*, λ*)=  1 μ*0 ( μ*0f0(x*) +  k ∑ i = 1 μ*if ′i(x*) ) =  1 μ*0 M′x(x*, μ*) = Θ. Наоборот, если теорема 6.8 верна, а x* — локальное решение задачи (1)–(2), то в качестве μ* можно взять набор (1, λ*), если x* — регулярная точка, и набор (0, α*), если векторы f ′1(x*),..., f ′k(x*) линейно зависимы: ∑ki=1α*if ′i(x*) = Θ. З а д а ч а  6.3. Приведите пример задачи с нерегулярной точкой минимума, в которой нельзя гарантировать отличие μ*0от нуля. Первые m уравнений системы, f(x) = Θ,   L′x(x, λ)= Θ, т. е. уравнение f(x) = Θ, очевидно, могут быть записаны в виде L′λ(x, λ)= Θ. Поэтому эта система переписывается следующим образом: L′λ(x, λ)= Θ,   L′x(x, λ)= Θ, или, что то же самое, L′(x, λ) = Θ. (10) Таким образом, (x*, λ*) — стационарная точка функции Лагранжа. В некотором смысле правило множителей Лагранжа сводит задачу о поиске условного минимума к безусловной задаче о поиске стационарной точки (см. (10)). Точка (x*, λ*) при этом не обязательно является точкой минимума функции Лагранжа, наоборот, в общей ситуации она является ее (функции Лагранжа) седловой точкой. З а д а ч а  6.4. Покажите, что подтверждающим последнее утверждение примером служит задача (1)–(2) с f0(x1, x2) = –x1 + x22и f1(x1, x2) = –x1 + x32. Для нерегулярных точек минимума правило множителей Лагранжа мало что дает, поскольку результат может не зависеть от минимизируемой функции f0: если μ*0= 0, то при любой f0 точка (x*, μ*) стационарна. 6.9. Одно достаточное условие локального минимума. Говорят, что линейный оператор A положительно определен на подпространстве E, если (Ax, x) > 0 при всех x ∈ E. Касательным подпространством к многообразию Ω в точке y называется множество TΩy = {x ∈ Rm: (f ′(y), x) = 0, i = 1, ..., k}. Касательной гиперплоскостью к многообразию Ω в точке y называется множество Ω′y = {x ∈ Rm: fi(y) + (f ′(y), x–y) = 0, i = 1, ..., k}. Теорема (достаточное условие минимума). Пусть F ∈ C2, а x* — регулярная стационарная точка функции Лагранжа, т. е., в частности, L′(x*, λ*) = Θ при некотором ненулевом λ* ∈ Rk. Тогда, если Lxx′′(x*, λ*)положительно определен на TΩx*, то точка x* является локальным решением задачи (1)–(2). Д о к а з а т е л ь с т в о.  Добавим к функции Лагранжа "штраф за нарушение ограничений (2)": N(x, λ, s) = L(x, λ) + s|| f(x)||2 З а д а ч а  6.5. Докажите, что (||f(x)||2)′ = 2f ′(x)f(x), а (||f(x)||2)′′ = 2[f ′(x)]*f ′(x), где * означает переход к сопряженному оператору. В силу задачи 6.5 и условий теоремы N′x(x*,λ*, s) = L′x(x*,λ*) + 2sf ′(x*)f(x*), а N′′xx(x*,λ*, s) = L′′xx(x*,λ*) + 2s[f ′(x)]*f ′(x). Покажем, что при достаточно больших s оператор N′′xx(x*,λ*, s) положительно определен. Для y ∈ Rm имеем (N′′xx(x*,λ*, s)y, y) = (L′′xx(x*,λ*)y, y) + 2s([f ′(x)]*f ′(x)y, y) = = (L′′xx(x*,λ*)y, y) +2s|| f ′(x*)||2. Тогда, если y ∈ TΩx*, т. е. f ′(x*)y = 0, то положительно (по условиям теоремы) первое слагаемое в правой части этого равенства. Если же y ∉ TΩx*, то при s бóльших некоторого s0 положительна вся сумма. З а д а ч а  6.6. Покажите, что s0 можно выбрать не зависящим от y. Таким образом, стационарная точка x* функции x → N(x, λ*, s) удовлетворяет при достаточно больших s условиям теоремы 2.5 и, следовательно, является ее локальным минимумом: N(x, λ*, s) ≥ N(x*, λ*, s) при x близких к x*. Остается заметить, что если точка x допустима, то N(x, λ*, s) = L(x, λ*) = f0(x) и поэтому f0(x) ≥ f0(x*). 6.10. Замечания о существовании и единственности решений. Поскольку в идейном плане утверждения, приводимые ниже, не доставляют ничего нового по сравнению с утверждениями пп. 2.6 и 2.7, мы формулируем их в виде задач и предоставляем читателю возможность доказать их. З а д а ч а  6.7. Пусть F ∈ C и при некотором α множество {x ∈ Ω: f0(x) ≤ α} не пусто и ограничено. Тогда задача (1)–(2) разрешима. Решение x* локальной условной задачи (1)–(2) называется локально единственным, если в некоторой его окрестности нет других локальных решений этой задачи. Регулярное решение x* называется невырожденным если L′′xx(x*,λ*) положительно определен на касательном подпространстве TΩx*. З а д а ч а  6.8. Докажите, что невырожденная точка минимума локально единственна. Перейдем к приближенным методам решения задачи (1)–(2). Мы изложим только основные идеи. 6.11. Методы решения задач с ограничениями типа равенств. Мы будем рассматривать ниже только регулярный случай. Один из естественных подходов к решению задач типа (1)–(2) основывается на необходимом условии экстремума — правиле множителей Лагранжа. Если бы можно было утверждать, что решению x* задачи (1)–(2) соответствует экстремум (x*, λ*) функции Лагранжа L, то к функции L можно было бы применять разработанные методы решения безусловных задач. Однако, так утверждать нельзя. В самом деле, если в точке x ограничения не выполняются, то за счет выбора λ функцию L (поскольку по λ она линейна) можно сделать как сколь угодно большой положительной, так и сколь угодно большой отрицательной. Поэтому естественно искать решение x* как первые m координат стационарной точки функции Лагранжа, например, методом Ньютона, для которого не важен тип стационарной точки (он одинаково хорошо ищет как экстремальные, так и седловые точки (см., напр., теорему 4.2 Таким способом мы приходим к методу Ньютона решения задач с ограничениями типа равенств — это просто метод Ньютона решения уравнения L′(x, λ) = Θ (в регулярном случае): L′(xn, λn) + L′′(xn, λn)(xn+1 – xn, λn+1 – λn) = Θ (см. уравнение (4.5)), или, в "координатной" форме L′x(xn,λn) + L′′xx(xn,λn)(xn+1 – xn) + L′′xλ(xn,λn)(λn+1 – λn) = Θ, L′λ(xn,λn) + L′′xλ(xn,λn)(xn+1 – xn) + L′′λλ(xn,λn)(λn+1 – λn) = Θ. Остается подставить в эти уравнения явные выражения производных функции Лагранжа (учитывая, в частности, что L′′λλ(xn,λn) = Θ): f ′0(xn)+ [f ′(xn)]*λn +  ( f ′′0(xn)+  k ∑ i = 1 λnif ′′i(xn) ) (xn+1 – xn) +  + [f ′(xn)]*(λn+1 – λn) = Θ, f(xn) + f ′(xn)(xn+1 – xn) = Θ и мы получаем m + k линейных уравнений для нахождения m + k неизвестных (xn+1, λn+1). З а д а ч а  6.9. Пользуясь теоремой 4.2, сформулируйте и докажите утверждение о сходимости метода Ньютона для задачи (1)–(2). Описанный метод обладает всеми достоинствами и всеми недостатками метода Ньютона решения безусловных задач, в частности, он лишь локально сходится и требует большого объема вычислений. Поэтому попытаемся модифицировать градиентный метод, приспособив его к решению условной задачи (1)–(2). Поскольку, как сказано выше, точка (x*, λ*) — это седловая точка функции Лагранжа, то естественно пытаться с помощью градиентного метода минимизировать ее по x, одновременно максимизируя ее по λ: xn+1 = xn – αL′x(xn,λn), λn+1 = λn + αL′λ(xn,λn), или, что то же, xn+1 = xn – α(f ′0(xn)+ [f ′(xn)]*λn), λn+1 = λn + αf(xn).

Можно доказать, что этот метод (его обычно называют методом Эрроу — Гурвица) при естественных ограничениях на гладкость и при условии положительной определенности оператора L′′xx(x*,λ*) локально линейно сходится.

Описанные методы относятся к разряду двойственных методов, поскольку в итерационном процессе участвуют как прямые (x), так и двойственные (λ) переменные.

Можно строить также прямые методы решения условных задач. Например, реализовать идею о том, что следующее приближение градиентного метода — это не слишком далеко отошедшее от предыдущей итерации решение линеаризованной задачи можно так. Приближение xn+1 ищется как минимум функции x → (f ′0(xn),x – xn) + α||x – xn||2 на касательной гиперплоскости Ω′xn. Здесь "штрафной член" α||x – xn||2 позволяет "минимизировать" линейную функцию x → (f ′0(xn),x – xn). Таким образом мы приходим к прямому методу

xn+1 = argmin [(f ′0(xn),x – xn) + α||x – xn||2],

(11)

fi(xn) + (f ′i(xn),x – xn) = 0,   i = 1, ..., k.

(12)

Ограничения (12) в этом методе — это, очевидно, линеаризации ограничений (2) в точке xn: минимум ищется на касательной гиперплоскости Ω′xn.

З а д а ч а  6.10. Пусть Pn — оператор ортогонального проектирования на касательную гиперплоскость Ω′xn. Докажите, что метод (11)–(12) может быть переписан в виде

xn+1 = Pn ( xn –  1 2α f ′0(xn) ) .

(Поэтому метод (11)–(12) часто называют методом проекции градиента).

Один из распространенных методов решения задач с ограничениями, с которым мы еще столкнемся — так называемый метод штрафов. Он позволяет сводить задачу с ограничениями к задаче без ограничений и суть его заключается в наказании за невыполнение ограничений. Именно, вместо минимизации функции f₀ с ограничениями (2) минимизируется функция

fs(x) = f0(x) + s||f(x)||2

без ограничений, в которой s — положительный параметр.

З а д а ч а  6.11. Пусть задача (1)–(2) имеет единственное решение x*, F ∈ C, а множество {x ∈ R^m: ||f_i(x)|| ≤ ε, i = 1, ..., k} ограничено. Докажите, что задача f ^s(x)→ min при достаточно больших s имеет решение, скажем x^s, и x^s → x* при s → ∞.

Поэтому задачу (1)–(2) можно решать как безусловную, полагая

xn = argmin f sn(x),

где sⁿ — некоторая неограниченно возрастающая последовательность. Недостаток этого метода для задачи с ограничениями типа равенств обусловлен тем, что при s → ∞ возрастает овражность функции f^s: около многообразия Ω образуется все более глубокий овраг (см. рис. 21) Поэтому важны как методы решения получающейся безусловной задачи, так и алгоритм выбора штрафа sⁿ.

Рис. 21.

File based on translation from T_EX by T_TH, version 3.05.
Created 9 Jun 2001, 117:22.