§ 6. Задачи с ограничениями типа равенств

В этом параграфе рассматривается одна из простейших задач условной оптимизации. Проводится теоретическое исследование. Описываются методы решения

6.1. Постановка задачи.

Напомним, что общая задача условной оптимизации выглядит так

f(x) ® min,   x О W,

где W — собственное подмножество R^m. Подкласс задач с ограничениями типа равенств выделяется тем, что множество W задается ограничениями вида

fi(x) = 0, где fi: Rm ®R (i = 1, ..., k). Таким образом, W = {x О Rm: fi(x) = 0, i = 1, ..., k}. В этом параграфе, как и в предыдущих, мы предполагаем, что все участвующие в рассмотрении функции достаточно гладкие. В общем случае множество W представляет собой гладкое (m-k)-мерное многообразие. Нам будет удобно писать у функции f индекс "0". Таким образом, задача оптимизации с ограничениями типа равенств записывается в виде f0(x) ® min, (1) fi(x) = 0,   i = 1, ..., k. (2) Если обозначить теперь через f функцию на Rm со значениями в Rk, координатная запись которой имеет вид f(x) = (f1(x), ..., fk(x)), то (1)–(2) можно также записать в виде f0(x) ® min,   f(x) = Q. Геометрически задача с ограничениями типа 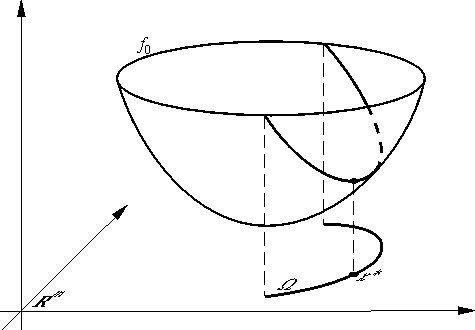равенств — это задача о поиске наинизшей точки графика функции f0 над многообразием W (см. рис. 19). Рис. 19. 6.2. Определения. Точки, удовлетворяющие всем ограничениям (т. е. точки множества W), обычно называют допустимыми. Допустимая точка x* называется условным минимумом функции f0 при ограничениях fi(x) = 0, i = 1, ..., k (или решением задачи (1)–(2)), если при всех допустимых точках x f0(x*) Ј f0(x). (3) Если (3) выполняется только для допустимых x, лежащих в некоторой окрестности Vx* точки x*, то говорят о локальном условном минимуме. Естественным образом определяются понятия условных строгих локального и глобального минимумов. З а д а ч а  6.1. Имеет ли задача x21+ x22® min, (x1 - 1)2 + x22= 1, (x1 + 1)2 + x22 = 1 решение? 6.3. Правило множителей Лагранжа. Описываемый ниже необходимый признак локального условного минимума был сформулирован Лагранжем. Определим F: Rm ® Rk+1, положив F(x) = (f0(x), f1(x), ..., fk(x)). Заданная на Rm×Rk+1 скалярная функция Лагранжа M по определению принимает значения в R и задается равенством M(x, m) = (m, F(x)) =  k е i = 0 mi fi(x)   (x О Rm, m О Rk+1).  Координаты вектора m, т. е. числа m0, m1, ..., mk называются множителями Лагранжа или двойственными переменными. Оказывается, имеет место следующая теорема, часто именуемая правилом множителей Лагранжа: Теорема. Пусть F О C1 и x* — локальный условный минимум функции f0 при ограничениях fi(x) = 0 (i = 1, ..., k). Тогда найдется ненулевой вектор m* такой, что x* является стационарной точкой функции x® M(x, m*): Mўx(x, m*)|x=x*=  k е i = 0 m*i f ўi(x*)= Q.   6.4. Обсуждение правила множителей Лагранжа. Начнем с геометрической интерпретации. Пусть для наглядности m = 2, а k = 1. В соответствии с теоремой 6.3, если 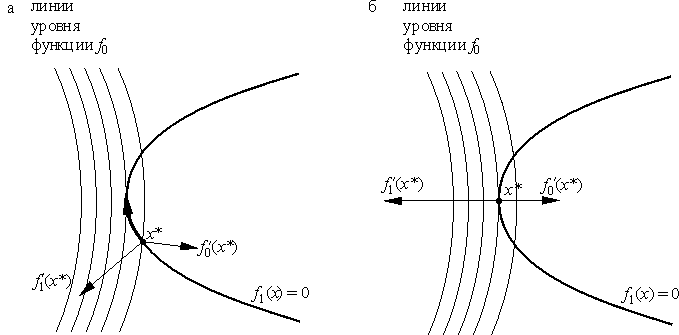x* — локальное решение задачи (1)–(2), то при некотором ненулевом m* О R2 m*0 f ў0(x*)+ m*1f ў1(x*)= Q. (4) Это равенство означает, что векторы f ў0(x*)и f ў1(x*)линейно зависимы. Теперь заметим, что -f ў0(x*)указывает направление наискорейшего убывания функции f0. Поэтому, если (4) не выполняется, т. е. векторы f ў0(x*)и f ў1(x*)не коллинеарны, то по многообразию W = {x О R2: f1(x*) = 0} можно сдвинуться, уменьшив значение f0 (в направлении, указанном жирной стрелкой на рис. 20а)). Если же x* — решение задачи (1)–(2), то этого сделать нельзя и (см. рис. 20б)) поэтому векторы f ў0(x*)и f ў1(x*)должны быть коллинеарны, т. е. при некотором m* № Q должно выполняться равенство (4). Рис. 20. Правило множителей Лагранжа доставляет необходимое условие локального условного минимума и поэтому позволяет искать точки, "подозрительные" на экстремум. В самом деле, для нахождения точки (x*, m*) О Rm+k+1, т. е. для нахождения m + k + 1 неизвестных, мы имеем m + k уравнений f(x) = Q,   Mўx(x, l)= Q. Поскольку, очевидно, множители Лагранжа можно искать с точностью до постоянного множителя, то в общей ситуации этих уравнений хватает для отыскания x*. 6.5. Доказательство теоремы 6.3. Допустим противное: x* — локальное решение задачи (1)–(2), а нужного m* не существует. Последнее означает, что векторы f0(x*), f1(x*), ..., fk(x*) линейно независимы, что, в свою очередь, влечет равенство rank ж з з з з з з и ¶f0(x*) ¶x1 ··· ¶fk(x*) ¶x1 : ··· : ¶f0(x*) ¶xm ··· ¶fk(x*) ¶xm ц ч ч ч ч ч ч ш  = k+1. Допустим, для определенности, что отличный от нуля минор (k+1)-го порядка образуют первые k + 1 строка этой матрицы: det ж з з з з з з и ¶f0(x*) ¶x1 ··· ¶fk(x*) ¶x1 : ··· : ¶f0(x*) ¶xk+1 ··· ¶fk(x*) ¶xk+1 ц ч ч ч ч ч ч ш  № 0. (5) Обозначим (x1, ..., xk+1) через x, а (xk+2, ..., xm) — через h: x = (x, h), x* = (x*, h*). Обозначим далее f0(x*) через a* и определим оператор F: Rk+1 ® Rk+1 формулой F(x) = F(x, h*). (6) Тогда, во-первых, F(x*) = (f0(x*), ..., fk(x*)) = (a*, 0, ..., 0) =def z* и, во-вторых, в силу (5), Fў(x*) невырожден. В силу теоремы об обратном отображении (см. любой курс математического анализа) в некоторой окрестности Vz* точки z* существует непрерывное обратное к F отображение Y: при всех z О Vz* F[Y(z)] = z. (7) В частности, это равенство имеет место для z = zs = (s + a*, 0, ..., 0) при всех достаточно малых s. Положим xs = (Y(zs), h*). Тогда (см. (6), (7)) (f0(xs), ..., fk(xs)) = F(xs) = F[Y(zs), h*] = = F[Y(zs)] = zs = (s + a*, 0, ..., 0). Таким образом, при достаточно малых s, во-первых, f0(xs) = s + f0(x*) (8) и, во-вторых, f1(xs) = ... = fk(xs) = 0. Последнее равенство означает, что точки xs являются допустимыми, а (8) (если взять s достаточно малым и отрицательным) — что x* не является условным локальным минимумом. Полученное противоречие доказывает теорему. 6.6. Обсуждение доказательства. Основную идею доказательства, приведенного выше можно, немного модифицировав, интерпретировать так. Разобьем переменные xi на две группы (y, z) О Rk×Rm-k так, чтобы из уравнения (2), т. е. из уравнения f(y, z) = Q можно было выразить y через z: y = j(z). Это можно сделать, поскольку f(y*, z*) = Q, а f ўy(y*, z*)= Q невырожден. Тогда задача (1)–(2) записывается в виде безусловной задачи f0(j(z), z) ® min,   z О Rm-k. (9) Теорема Ферма для задачи (9) при этом порождает теорему 6.3. З а д а ч а  6.2. Проведите аккуратные рассуждения. 6.7. Регулярные точки. Допустимая точка x задачи (1)–(2) называется регулярной, если векторы {f ўi(x)}ki=1линейно независимы. Оказывается, что если x* — регулярная точка минимума, то в векторе m* можно считать m*0 считать ненулевым, а поскольку множители Лагранжа определяются с точностью до множителя, можно считать, что m*0 = 1. Чтобы сформулировать это утверждение более точно, введем следующие обозначения. Пусть l О Rk, а функция Лагранжа в регулярном случае определяется равенством L(x, l) = f0(x) + (l, f(x)) = f0(x) +  k е i = 1 li fi(x)   (x О Rm, l О Rk). Очевидно, L(x, l) = M(x, m), где m = (1, l). 6.8. Теорема (правило множителей Лагранжа в регулярном случае). Пусть F О C1, а x* — регулярное локальное решение задачи (1)–(2). Тогда найдется ненулевой вектор l* О Rk такой, что Lўx(x*, l*)= Q. Д о к а з а т е л ь с т в о.  Покажем, что теоремы 6.3 и 6.8 вытекают друг из друга (для доказательства теоремы 6.8 достаточно, разумеется, импликации "теорема 6.3 Ю теорема 6.8"; однако для полноты изложения мы докажем и обратное утверждение). Итак, пусть x* — регулярная точка минимума, а m* — вектор, фигурирующий в теореме 6.3. Тогда, если m*0 = 0, то в силу этой теоремы Q = Mўx(x*,m*) =  k е i = 0 m*if ўi(x*)=  k е i = 0 m*if ўi(x*),  а поскольку не все m*i (i = 1, ..., k) равны нулю, последнее равенство противоречит регулярности x*. Поэтому m*0 № 0. Теперь в качестве искомых l*iможно взять m*i/m*0: Lўx(x*, l*)=  1 m*0 ж и m*0f0(x*) +  k е i = 1 m*if ўi(x*) ц ш =  1 m*0 Mўx(x*, m*) = Q. Наоборот, если теорема 6.8 верна, а x* — локальное решение задачи (1)–(2), то в качестве m* можно взять набор (1, l*), если x* — регулярная точка, и набор (0, a*), если векторы f ў1(x*),..., f ўk(x*) линейно зависимы: еki=1a*if ўi(x*) = Q. З а д а ч а  6.3. Приведите пример задачи с нерегулярной точкой минимума, в которой нельзя гарантировать отличие m*0от нуля. Первые m уравнений системы, f(x) = Q,   Lўx(x, l)= Q, т. е. уравнение f(x) = Q, очевидно, могут быть записаны в виде Lўl(x, l)= Q. Поэтому эта система переписывается следующим образом: Lўl(x, l)= Q,   Lўx(x, l)= Q, или, что то же самое, Lў(x, l) = Q. (10) Таким образом, (x*, l*) — стационарная точка функции Лагранжа. В некотором смысле правило множителей Лагранжа сводит задачу о поиске условного минимума к безусловной задаче о поиске стационарной точки (см. (10)). Точка (x*, l*) при этом не обязательно является точкой минимума функции Лагранжа, наоборот, в общей ситуации она является ее (функции Лагранжа) седловой точкой. З а д а ч а  6.4. Покажите, что подтверждающим последнее утверждение примером служит задача (1)–(2) с f0(x1, x2) = -x1 + x22и f1(x1, x2) = -x1 + x32. Для нерегулярных точек минимума правило множителей Лагранжа мало что дает, поскольку результат может не зависеть от минимизируемой функции f0: если m*0= 0, то при любой f0 точка (x*, m*) стационарна. 6.9. Одно достаточное условие локального минимума. Говорят, что линейный оператор A положительно определен на подпространстве E, если (Ax, x) > 0 при всех x О E. Касательным подпространством к многообразию W в точке y называется множество TWy = {x О Rm: (f ў(y), x) = 0, i = 1, ..., k}. Касательной гиперплоскостью к многообразию W в точке y называется множество Wўy = {x О Rm: fi(y) + (f ў(y), x-y) = 0, i = 1, ..., k}. Теорема (достаточное условие минимума). Пусть F О C2, а x* — регулярная стационарная точка функции Лагранжа, т. е., в частности, Lў(x*, l*) = Q при некотором ненулевом l* О Rk. Тогда, если Lxxўў(x*, l*)положительно определен на TWx*, то точка x* является локальным решением задачи (1)–(2). Д о к а з а т е л ь с т в о.  Добавим к функции Лагранжа "штраф за нарушение ограничений (2)": N(x, l, s) = L(x, l) + s|| f(x)||2 З а д а ч а  6.5. Докажите, что (||f(x)||2)ў = 2f ў(x)f(x), а (||f(x)||2)ўў = 2[f ў(x)]*f ў(x), где * означает переход к сопряженному оператору. В силу задачи 6.5 и условий теоремы Nўx(x*,l*, s) = Lўx(x*,l*) + 2sf ў(x*)f(x*), а Nўўxx(x*,l*, s) = Lўўxx(x*,l*) + 2s[f ў(x)]*f ў(x). Покажем, что при достаточно больших s оператор Nўўxx(x*,l*, s) положительно определен. Для y О Rm имеем (Nўўxx(x*,l*, s)y, y) = (Lўўxx(x*,l*)y, y) + 2s([f ў(x)]*f ў(x)y, y) = = (Lўўxx(x*,l*)y, y) +2s|| f ў(x*)||2. Тогда, если y О TWx*, т. е. f ў(x*)y = 0, то положительно (по условиям теоремы) первое слагаемое в правой части этого равенства. Если же y П TWx*, то при s бóльших некоторого s0 положительна вся сумма. З а д а ч а  6.6. Покажите, что s0 можно выбрать не зависящим от y. Таким образом, стационарная точка x* функции x ® N(x, l*, s) удовлетворяет при достаточно больших s условиям теоремы 2.5 и, следовательно, является ее локальным минимумом: N(x, l*, s) і N(x*, l*, s) при x близких к x*. Остается заметить, что если точка x допустима, то N(x, l*, s) = L(x, l*) = f0(x) и поэтому f0(x) і f0(x*). 6.10. Замечания о существовании и единственности решений. Поскольку в идейном плане утверждения, приводимые ниже, не доставляют ничего нового по сравнению с утверждениями пп. 2.6 и 2.7, мы формулируем их в виде задач и предоставляем читателю возможность доказать их. З а д а ч а  6.7. Пусть F О C и при некотором a множество {x О W: f0(x) Ј a} не пусто и ограничено. Тогда задача (1)–(2) разрешима. Решение x* локальной условной задачи (1)–(2) называется локально единственным, если в некоторой его окрестности нет других локальных решений этой задачи. Регулярное решение x* называется невырожденным если Lўўxx(x*,l*) положительно определен на касательном подпространстве TWx*. З а д а ч а  6.8. Докажите, что невырожденная точка минимума локально единственна. Перейдем к приближенным методам решения задачи (1)–(2). Мы изложим только основные идеи. 6.11. Методы решения задач с ограничениями типа равенств. Мы будем рассматривать ниже только регулярный случай. Один из естественных подходов к решению задач типа (1)–(2) основывается на необходимом условии экстремума — правиле множителей Лагранжа. Если бы можно было утверждать, что решению x* задачи (1)–(2) соответствует экстремум (x*, l*) функции Лагранжа L, то к функции L можно было бы применять разработанные методы решения безусловных задач. Однако, так утверждать нельзя. В самом деле, если в точке x ограничения не выполняются, то за счет выбора l функцию L (поскольку по l она линейна) можно сделать как сколь угодно большой положительной, так и сколь угодно большой отрицательной. Поэтому естественно искать решение x* как первые m координат стационарной точки функции Лагранжа, например, методом Ньютона, для которого не важен тип стационарной точки (он одинаково хорошо ищет как экстремальные, так и седловые точки (см., напр., теорему 4.2 Таким способом мы приходим к методу Ньютона решения задач с ограничениями типа равенств — это просто метод Ньютона решения уравнения Lў(x, l) = Q (в регулярном случае): Lў(xn, ln) + Lўў(xn, ln)(xn+1 - xn, ln+1 - ln) = Q (см. уравнение (4.5)), или, в "координатной" форме Lўx(xn,ln) + Lўўxx(xn,ln)(xn+1 - xn) + Lўўxl(xn,ln)(ln+1 - ln) = Q, Lўl(xn,ln) + Lўўxl(xn,ln)(xn+1 - xn) + Lўўll(xn,ln)(ln+1 - ln) = Q. Остается подставить в эти уравнения явные выражения производных функции Лагранжа (учитывая, в частности, что Lўўll(xn,ln) = Q): f ў0(xn)+ [f ў(xn)]*ln +  ж и f ўў0(xn)+  k е i = 1 lnif ўўi(xn) ц ш (xn+1 - xn) +  + [f ў(xn)]*(ln+1 - ln) = Q, f(xn) + f ў(xn)(xn+1 - xn) = Q и мы получаем m + k линейных уравнений для нахождения m + k неизвестных (xn+1, ln+1). З а д а ч а  6.9. Пользуясь теоремой 4.2, сформулируйте и докажите утверждение о сходимости метода Ньютона для задачи (1)–(2). Описанный метод обладает всеми достоинствами и всеми недостатками метода Ньютона решения безусловных задач, в частности, он лишь локально сходится и требует большого объема вычислений. Поэтому попытаемся модифицировать градиентный метод, приспособив его к решению условной задачи (1)–(2). Поскольку, как сказано выше, точка (x*, l*) — это седловая точка функции Лагранжа, то естественно пытаться с помощью градиентного метода минимизировать ее по x, одновременно максимизируя ее по l: xn+1 = xn - aLўx(xn,ln), ln+1 = ln + aLўl(xn,ln), или, что то же, xn+1 = xn - a(f ў0(xn)+ [f ў(xn)]*ln), ln+1 = ln + af(xn).

Можно доказать, что этот метод (его обычно называют методом Эрроу — Гурвица) при естественных ограничениях на гладкость и при условии положительной определенности оператора Lўўxx(x*,l*) локально линейно сходится.

Описанные методы относятся к разряду двойственных методов, поскольку в итерационном процессе участвуют как прямые (x), так и двойственные (l) переменные.

Можно строить также прямые методы решения условных задач. Например, реализовать идею о том, что следующее приближение градиентного метода — это не слишком далеко отошедшее от предыдущей итерации решение линеаризованной задачи можно так. Приближение xn+1 ищется как минимум функции x ® (f ў0(xn),x - xn) + a||x - xn||2 на касательной гиперплоскости Wўxn. Здесь "штрафной член" a||x - xn||2 позволяет "минимизировать" линейную функцию x ® (f ў0(xn),x - xn). Таким образом мы приходим к прямому методу

xn+1 = argmin [(f ў0(xn),x - xn) + a||x - xn||2],

(11)

fi(xn) + (f ўi(xn),x - xn) = 0,   i = 1, ..., k.

(12)

Ограничения (12) в этом методе — это, очевидно, линеаризации ограничений (2) в точке xn: минимум ищется на касательной гиперплоскости Wўxn.

З а д а ч а  6.10. Пусть Pn — оператор ортогонального проектирования на касательную гиперплоскость Wўxn. Докажите, что метод (11)–(12) может быть переписан в виде

xn+1 = Pn ж и xn -  1 2a f ў0(xn) ц ш .

(Поэтому метод (11)–(12) часто называют методом проекции градиента).

Один из распространенных методов решения задач с ограничениями, с которым мы еще столкнемся — так называемый метод штрафов. Он позволяет сводить задачу с ограничениями к задаче без ограничений и суть его заключается в наказании за невыполнение ограничений. Именно, вместо минимизации функции f₀ с ограничениями (2) минимизируется функция

fs(x) = f0(x) + s||f(x)||2

без ограничений, в которой s — положительный параметр.

З а д а ч а  6.11. Пусть задача (1)–(2) имеет единственное решение x*, F О C, а множество {x О R^m: ||f_i(x)|| Ј e, i = 1, ..., k} ограничено. Докажите, что задача f ^s(x)® min при достаточно больших s имеет решение, скажем x^s, и x^s ® x* при s ® Ґ.

Поэтому задачу (1)–(2) можно решать как безусловную, полагая

xn = argmin f sn(x),

где sⁿ — некоторая неограниченно возрастающая последовательность. Недостаток этого метода для задачи с ограничениями типа равенств обусловлен тем, что при s ® Ґ возрастает овражность функции f^s: около многообразия W образуется все более глубокий овраг (см. рис. 21) Поэтому важны как методы решения получающейся безусловной задачи, так и алгоритм выбора штрафа sⁿ.

Рис. 21.

File based on translation from T_EX by T_TH, version 3.05.
Created 9 Jun 2001, 117:22.