 |
1.4.1. Деформация сплошной среды |  |
Пусть x = g(x, t) — движение сплошной среды. Разумеется, при движении первоначальная конфигурация W0 сплошной среды переходит в "деформированную" конфигурацию Wt, при которой изменяется взаимное положение частиц сплошной среды. Зафиксируем некоторую частицу p0 О W0. Тогда ее положение в нулевой момент времени есть x0, а в момент времени t — x0 = g(x0, t). Вектор w0 = x0 – x0 называется вектором перемещения частицы p0. Пусть e1 О S — произвольный орт, x1 = x0 +
se1, а x1 = g(x1, t) (s > 0) (см. рис. 4.1).
Относительным удлинением в направлении e1 называется число
| l(e) = |
lim
s®0 | |x1 – x0| – |x1 – x0|
|x1 – x0| | . |
|
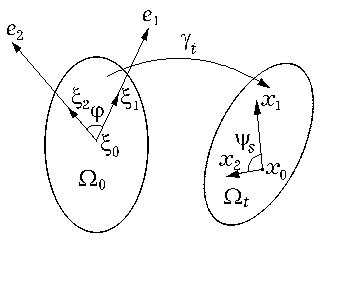
Рис. 4.1.
Пусть теперь e2 О
S, x2 = x0 + se2, x2 = g(x2, t), j — угол между векторами x1 – x0 и x2 – x0 (или, что то же, между ортами e1 и
e2), а ys — угол между векторами x1 – x0 и x2 – x0:
cos ys =
(x1 – x0)·(x2 – x0)/[|x1 – x0|·|x2 – x0|]
(см. рис. 4.1). Относительным сдвигом направлений e1 и e2 называется число
| t(e1, e2) = |
lim
s®0 | ys – j. |
|
Относительные удлинения и сдвиги полностью характеризуют деформации малой окрестности частицы p0, поскольку описывают, как изменяются расстояния и углы при движении сплошной среды.




