Для задач, возникающих при математическом моделировании диффузии ограниченной плазмы через магнитное поле, методами нелинейного анализа доказана разрешимость краевой задачи Дирихле для равномерно эллиптической системы с нелокальными нелинейностями. Получены достаточные условия существования и единственности классического стационарного решения, построена его область притяжения. Для нелинейных параболических уравнений теплопроводности с неявным вырождением доказано существование новых точных, анизотропных по пространственным переменным, явных решений в замкнутом виде. Показана инвариантность уравнения быстрой диффузии в двумерном координатном пространстве и проведена его редукция к одномерному по пространственной переменной аналогу, построены новые точные решения уравнения (рис.1). В отличие от известных результатов, предложенный подход позволяет свести построение нижних и верхних решений к конечномерным задачам и тем самым определить эти решения в явном виде.
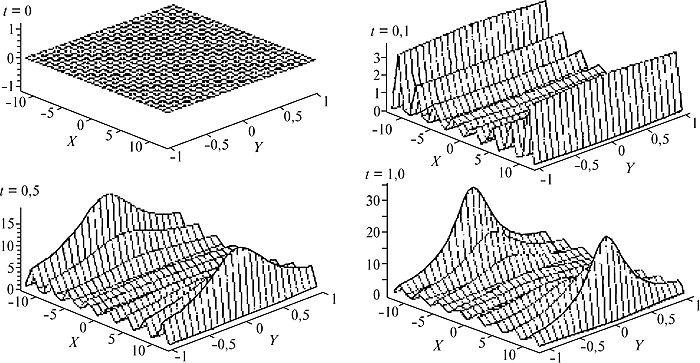 Рис. 1. Графики решения уравнения быстрой диффузии в различные моменты времени.
|


