Для систем с широтно-импульсным управлением на основе метода векторных функций Ляпунова (ВФЛ) получены конструктивные условия диссипативности, явно выраженные через параметры системы. Разработаны алгоритмы вычисления строгих количественных оценок предельного множества, области притяжения и времени достижения требуемого уровня точности, доведенные до формул, применимых в инженерной практике, и в отличие от мирового уровня учитывающие нелинейности и погрешности измерителей, исполнительных органов, модуляционной характеристики, формы импульсов и неопределенности внешних воздействий. При решении задачи применено двухэтапное использование ВФЛ (разные ВФЛ для больших и малых отклонений) и непосредственное построение дискретной системы сравнения, минуя дискретизацию исходной модели, что позволило получить более точные оценки качества. Выполнены приложения к исследованию режимов реактивного успокоения космических аппаратов (типа спутников связи), особенностями которых являются значительное влияние упругости конструкции, наличие низких собственных частот с малыми декрементами и сравнительно большое запаздывание в формировании импульсов. Благодаря использованию математической модели, описывающей реальные системы более точно по сравнению с известными, показана возможность гарантированной точности успокоения.
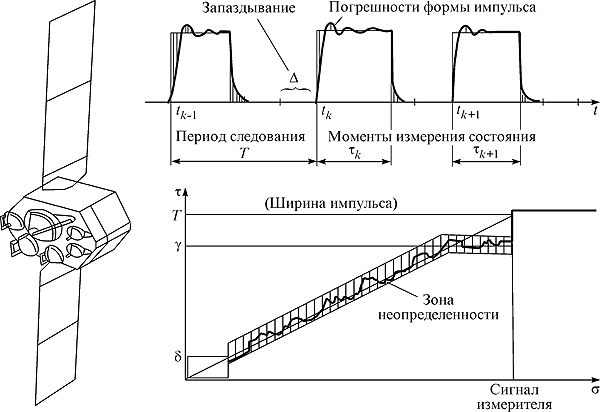 Рис. 1. Режим успокоения космических летательных аппаратов класса спутников связи.
|


